“I think I can safely say that NOBODY understands quantum mechanics.”
- Physicist Richard Feynman, winner of the 1965 Nobel Prize for his groundbreaking theory of quantum electrodynamics.
Research into quantum physics applications such as computing, communications, simulation and sensing is moving at a frantic pace. Its promise for orders of magnitude advances in cryptanalysis, secure communications, prediction of materials properties and spectroscopy has caught the attention of many national governments and private investors eager to fund further research.
So, what is the big deal?
A regular digital computer performs data processing tasks by manipulating bits; each bit can have a value of one or zero. A quantum physicist would say this is a “classical” implementation of computing. A “quantum” implementation of a computer manipulates quantum bits (qubits). Qubits can have a value of one, zero or both simultaneously. When the bit is simultaneously a one and a zero, the bit is said to be in a state of superposition. Moreover, the state of one qubit can influence another qubit, even if they are separated by great distance, in this case, the states are said to be entangled. Superposition and entanglement are at the heart of quantum computing and provide capabilities that can speed the types of calculation required for cryptanalysis from years to minutes.
To understand how a quantum computer works, we need to understand the properties of an electron, how electrons behave in the presence of electromagnetic (EM) fields and how this is used within a qubit. We can then understand the implementation of the qubit and how to control and measure its state. Finally, we will address how qubits interact with each other and how, when put all together, they can perform computing. Putting Richard Feynman’s comments regarding quantum physics to one side, we can more easily understand how to control and manipulate data and perform computations with a fairly basic understanding of RF/microwave signal behavior, especially transmission lines and the inductor/capacitor (LC) tuned circuit.
HOW ATOMS AND ELECTRONS WORK
Quantum computing is built on the work of the great physicists: Planck for saying energy is not contiguous but quantized, Einstein for discovering the photoelectric effect, Bohr and Rutherford for applying Planck’s quantized energy rules to electron orbits, Louis de Broglie for proposing that electron particles also have wave properties and Schrödinger for introducing probabilities into the energy states of an electron.
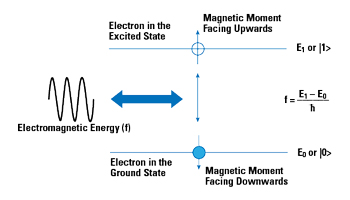
Figure 1 The frequency of applied EM energy causes electrons to move from one energy state to another.
Each atomic orbital is represented by an energy level measured in electron volts (eV), with the lowest orbit called the ground state. As a particle can also be a wave, its energy level has a frequency equal to the energy level in eV divided by Planck’s constant (the quantization constant). Consider Figure 1. If we want the electron to move to a higher energy state, we apply EM energy at a frequency equal to the desired energy level minus the current energy level, divided by Planck’s constant. The electron will absorb the energy and jump to the next quantum energy level. Once the energy is removed, it will fall back to its original level, emitting the energy at the frequency previously absorbed. The frequency of the stimulus - not the amplitude - is key. Increasing the amplitude will not cause the electron to move to a higher energy level, increasing the frequency will. With this understanding, if we can constrain the energy levels to two, we have the fundamental building blocks for manipulating ones and zeros with a single electron.
