Part I of this article1 analyzed the driving circuits and methods for power amplifiers, using a low frequency approximation. This second part deals with the driving problem at high frequencies. Using a simple yet effective (for this purpose) active device model, the influence of the intrinsic feedback capacitance is analyzed for the most important and used amplification classes, including high efficiency switching-based classes, such as class-E. The widely used sinusoidal drive is compared to a square voltage drive for high efficiency power amplifiers operating at high frequencies.
Amplification Classes Analysis: High Frequency Approximation
A low frequency transistor model was used in the first part of this work. This first approximation helps to understand some driving effects. However, in order to achieve more accurate results, a simple but accurate high frequency model is required. The model used here is similar to the one used in Part I but takes into account the most important effect taking place at high frequencies. The main characteristics of this model can be summarized:
• CGD is not neglected. In fact, CGD has a remarkable effect on the amplifier performance.
• The rest of the model elements are shared with the low frequency model. The capacitances are kept constant, even CGD.
Class-A Amplifier Analysis: High Frequency Approximation
The classical class-A analysis for small-signal amplifiers2 and power amplifiers3 can be used with the proposed high frequency model. These theories can be used even for large voltage and current excursions because all the elements of the model are kept constant (linear behavior). The transconductance gm is also constant.
Furthermore, the Miller theorem can also be used to simplify the analysis. Therefore, the capacitance CGD between the drain and gate terminals gets translated into a capacitance across gate and source that can be added to CGS (as a capacitance in parallel with CDS). The equivalent circuit used for this analysis is shown in Figure 1.
 | ||
| Fig. 1 Class-A amplifier equivalent circuit: high frequency approximation. | ||
Therefore, the analysis shown in Part 1, “Class-A Amplifier,” can be used again. The only difference is in the equivalent input capacitance because it is larger than the capacitance of the low frequency model. Using a series input resonant circuit, the driving power can be calculated as

where
K1 = input Miller coefficient
Equation 1 shows that P'G is larger than PG (driving power calculated for the low frequency model). In practice, the nonlinear nature of CGD (and the other intrinsic capacitances) and the transconductance gm contribute to some variations in both power driving calculations and voltage and current waveforms.
Classes AB, B and C Analysis: High Frequency Approximation
CGD increases the driving power required by amplifiers operating in reduced conduction angle classes. The equivalent model of the active device is modified by CGD like in the class-A amplifier. Therefore, similar conclusions can be derived. The results shown in the low frequency approximation in the analysis of classes AB, B and C of Part I can be applied, accounting for the changes introduced by CGD. A recent paper4 analyzes a simple, yet effective, active device model using some approximations, and the interested reader may review it for further explanations on this topic.
The contribution of CGD has a more severe impact on high efficiency classes based on nonlinear (switching) behavior. This effect will be analyzed in the following sections.
High Efficiency Classes Analysis: High Frequency Approximation
It was mentioned previously that CGD produces important changes in RF and microwave device behavior. Obviously these changes also affect the driving requirements of high efficiency power amplifiers, especially those based on switching such as class-E. Switching-based amplification classes are characterized by working with strong nonlinear conditions at their output network. The capacitance across the drain and gate, CGD, transfers this nonlinear behavior to the input circuit. To show this effect, a class-E amplifier operating in nominal conditions at high frequencies will be analyzed. The driving signal will be a square wave voltage.
Low Source Impedance Square Voltage Source Driving Class-E Amplifier
The output waveforms of a class-E amplifier show remarkable changes along a complete period. Figure 2 shows the equivalent circuit of a class-E amplifier during the cutoff and saturation intervals. The drain-to-source voltage vDS(t) and the gate current iG(t) are also shown for a complete period. The most significant instants are marked with encircled numbers over the drain-to-source voltage vDS(t).
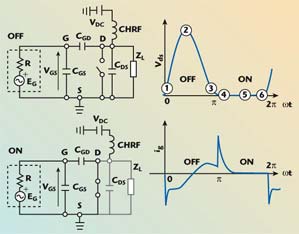 | ||
| Fig. 2 Class-E equivalent circuit and waveforms for square wave drive. | ||
If ZL is the load impedance required for nominal class-E operation,4 this load must fulfill the following relation at the fundamental frequency for nominal conditions of operation

where
XCOUT is the equivalent output capacitance. It is larger than CDS, as will be shown later.
The impedance ZL must be high for the harmonics.
The device operates as an ideal switch, that is: RON = 0 during saturation, ROFF = infinite during cutoff.
The amplifier duty cycle is 50 percent.
The equivalent circuits of Figure 3 show the charging and discharging processes of the intrinsic device capacitances during the most significant period instants. These significant instants are selected around the cutoff and saturation instants. They are indicated with encircled numbers in the drain-to-source vDS(t) plot.
 | ||
| Fig. 3 Intrinsic capacitances charging process. | ||
From the last two figures, the following consequences are derived:
• During the OFF interval (instants 1, 2 and 3), the capacitance CGD is charged and discharged as a consequence of the input driving voltage vGS(t) and the voltage across CDS.
• During the OFF interval, the driving source discharges CGS. CGD is in parallel with CDS because of the low source impedance of the driving source; thus, CGD experiences the same charging and discharging process as CDS. Therefore, during the OFF interval the output equivalent capacitance can be considered COUT = CDS + CGD (in this circuit).
• The gate current iG(t) during the OFF interval is composed of the CGS discharging current and the charging and discharging CGD current (this current is positive and negative during the OFF period).
• Because of the large value of vDS(t) compared to vGS(t) the charge stored at CGD is similar to the charge stored at CGS even though CGS
• During the ON interval (instants 4, 5 and 6), the saturation resistance is low, so the driving source must charge CGS in parallel with CGD (only CGS was charged with the low frequency model). CGS is usually several times larger than CGD.
• During the ON interval, the gate current is composed of both the charging currents of CGS and CGD (in parallel).
From the described conditions, it can be derived that CGD transfers the nonlinear behavior of the output circuit to the input circuit. Thus, the input circuit conditions of the class-E amplifier at RF and microwaves are nonlinear, even though the device inherent capacitances are constant and independent of the voltage across them. Therefore, to optimize the power amplifier efficiency, the driving circuit must take these results into account.
Sinusoidal Voltage Driving with Input Serial Resonant Circuit
A square wave, low source resistance voltage generator can drive and handle the associated nonlinear currents at the device input, but there are serious technological limits to the manufacture of such drivers at RF and microwave frequencies. This is the reason why a sinusoidal voltage drive is the most popular driving method at high frequencies. The strong input capacitive nature of the device requires resonant input circuits to minimize power losses.
Voltage Source and Series Resonant Input Circuit
This driver consists of a low internal impedance sinusoidal voltage source and a series coil which resonates the equivalent input capacitance of the active device. This circuit provides a low source impedance at the fundamental frequency and a high source impedance at the harmonics. Therefore, only a sinusoidal current iG(t) can flow through the gate terminal. Obviously, this sinusoidal current is not compatible with the nonlinear behavior of the input amplifier circuit.
In practice, the main difference observed when this kind of drive is used instead of a low source impedance square drive is a slight change of the output circuit tuning. This effect is combined with a decrease of both output power and efficiency. Although the gate current iG(t) is forced to be sinusoidal, there is no need for the gate-to-source voltage vGS(t) to be sinusoidal also. The shape of vGS(t) depends on the input circuit features and the nonlinear behavior of the active device input.
The gate current iG(t) and drain-to-source voltage vDS(t) waveforms obtained with sinusoidal resonant driving are shown in Figure 4. The same waveforms obtained with a low source impedance square voltage source are also shown. The drain-to-source voltage vDS(t) shows the tuning change effect on the output circuit.
 | ||
| Fig. 4 Class-E waveforms; (a) low impedance square voltage driving and (b) resonant sinusoidal voltage driving. | ||
Current Source and Parallel Resonant Input Circuit
This drive system is the dual of the previous one. It is made of a high internal impedance sinusoidal current source with a parallel coil to resonate the equivalent input capacitance of the active device. From a theoretical point of view, this circuit is best adapted to the conditions at the input of a high efficiency amplifier. The parallel resonant circuit exhibits a high load impedance at the operating frequency and short-circuits at the harmonics. This source impedance favors a sinusoidal gate-to-source voltage vGS(t) with a non-sinusoidal gate current iG(t).
Nevertheless, from a practical point of view, the design of current sources capable of sourcing and sinking large currents at high frequencies is not an easy task. The gate terminal of a high frequency MOSFET exhibits a very low input impedance. This fact, combined with inductive package parasitics and bonding wires, makes the implementation of parallel resonant circuits difficult.
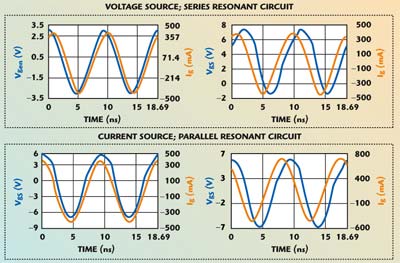 | ||
| Fig. 5 Input waveforms resulting from sinusoidal driving with series and parallel resonances. | ||
Figure 5 shows a complete set of voltages and currents obtained by harmonic balance simulation in a commercial LDMOS (Motorola MRF182). Sinusoidal driving was used with series and parallel resonant input circuits. The waveforms depicted are the gate-to-source voltage vGS(t), gate current iG(t), driving source voltage vGEN(t) and driving source current iGEN(t). The simulation circuit uses the same load and supply voltage for both serial and parallel input resonant circuits. Output power POUT, driving power PIN and drain efficiency ![]() D are displayed in Table 1.
D are displayed in Table 1.
 | ||
From a practical point of view, the results obtained for both circuits are quite similar, but the implementation of the parallel resonant driving circuit may be difficult at high frequencies. Something similar happens with the implementation of tuned loads for true class-B amplifiers at high frequencies.
Class-E and Class-A Power Amplifier Comparison at High Frequencies
In order to estimate the gain losses of a high frequency class-E amplifier versus a class-A amplifier, using the same device (MRF182), at the same frequency (100 MHz), output power level POUT (20 W) and supply voltage VDC (24 V), two amplifiers have been designed and simulated: a class-A power amplifier and a class-E amplifier with square voltage drive. The class-A amplifier has been heavily driven, but avoids saturation. Its load has been designed using the Cripps method to achieve a similar output power POUT than its class-E counterpart. The class-E amplifier uses the same load as the sinusoidal driven amplifier shown in the previous section, but is driven with a low internal impedance (3 Ω) square voltage source. Both amplifiers operate at 100 MHz. Harmonic balance analysis is used with the Motorola MRF182 manufacturer nonlinear model. The most significant waveforms of these amplifiers are depicted in Figure 6. The most important results are displayed in Table 1.
 | ||
| Fig. 6 Input wavefroms resulting from class-A sinusoidal resonant driving and square wave driving. | ||
From this data it is easy to derive that the square voltage driving method is the most effective for this amplifier. A gain improvement of almost 5 dB is obtained compared with the sinusoidal driving results and with better drain efficiency, too (but it was mentioned before that square wave driving is hard to implement at high frequencies). Comparing class-A results with class-E with sinusoidal driving, a gain reduction of 8 dB is observed while the drain efficiency is doubled.
Conclusion
An analysis of the most important driving methods for power amplifiers at high frequencies has been presented and the following few conclusions have been obtained:
- Sinusoidal driving of class-A power amplifiers is optimum and reasonable because the pursued output waveforms (voltage and current) are also sinusoidal. Although several nonlinear effects are present because of non-constant transconductance and intrinsic capacitances, all these effects can be tolerated by this amplification class without excessive degradation.
- Sinusoidal driving of reduced conduction angle classes (AB, B and C) is practical and easy to implement, but it leads to gain losses. The combination of sinusoidal voltage driving with the nonlinear transfer characteristic of a MOS device leads to a gain loss less than 3 dB in a class-B amplifier. These losses can be tolerated if the device gain is high. A special driving circuit design to avoid these losses is probably not worthwhile.
- Driving of high efficiency RF and microwave power amplifiers has not been covered in depth by literature, especially driving methods for switching-based amplification classes. Significant articles have been published for high efficiency power amplifier driving at low frequencies, but their conclusions can hardly be used at high frequencies for two reasons: device switching limitations and the influence of the capacitance across the drain and gate terminals CGD.
- The energy required to switch active devices operating in high efficiency amplifiers, like class-E, is higher than the energy required to drive these devices operating in other amplification classes like class-A. Therefore, it is important to optimize the driver circuit in order to avoid unnecessary energy wasting and further gain reduction.
- Sinusoidal driving has been used to overcome technological limitations of square wave driver circuits for high efficiency amplifiers at high frequencies. But using sinusoidal driving requires the device to be overdriven in order to keep the current fall times low and drain efficiency high. Overdriving implies using more energy than the minimum required for device switching. This fact further reduces the gain of high efficiency amplifiers.
- Driving methods for high efficiency RF and microwave power amplifiers requires further research and the development of new driving circuits. Also, the characterization of high frequency active power devices must be improved. Manufacturers should take into account the increasing trend of using high frequency power devices in high efficiency power amplifiers. Therefore, more useful parameters should be included in transistor data sheets to calculate device driving requirements in such environments.
-
Acknowledgment
This work was supported by project TIC2001-3839-C03 of the Spanish National Board of Scientific and Technology Research (MCYT).
References
- F.J. Ortega-González, “High Efficiency Power Amplifier Driving Methods and Circuits: Part I,” Microwave Journal, Vol. 47, No. 4, April 2004, pp. 22–38.
- G. Gonzalez, Microwave Transistor Amplifiers: Analysis and Design, Second Edition, Prentice-Hall, Upper Saddle River, NJ, 1997.
- S.C. Cripps, RF Power Amplifiers for Wireless Communications, Artech House Inc., Norwood, MA, 1999.
- J. Walker, “Analytic Expressions for the Optimum Source and Load Impedance and Associated Large-signal Gain of an RF Power Transistor,” 2003 IEEE MTT-S International Microwave Symposium Digest, 2003, pp. 1725–1728.
- F.H. Raab and N.O. Sokal, “Transistor Power Losses in the Class-E Tuned Power Amplifier,” IEEE Journal of Solid State Circuits, Vol. SC-13, April 1983, pp. 181–192.
Francisco Javier Ortega-González received his Ingeniero de Telecomunicación degree and his PhD degree from the Universidad Politécnica de Madrid. He is currently a professor at the E.U.I.T. de Telecomunicación of Universidad Politécnica de Madrid and leads its Radio Engineering Group (GIRA). His main research interests include high frequency and microwave circuit design, radar, digital communications, and wireless and datagram networks embedding. He has extensive experience directing and participating in several research projects financed by public and private companies. He can be contacted via e-mail at fjortega@diac.upm.es.
