The state-of-the-art indoor wireless systems operating at microwave frequencies (approximately 2.45 and 5.5 GHz) have been standardized in conformance with different multiplexing schemes and modulation techniques. The underlying design considerations1,2 aim at realizing robust operation of several interconnected and coexisting hosts3 across RF links. These links are designated to serve different applications and meet distinct standards as well as conform to ad hoc compliance requirements.
Notwithstanding the comprehensive and proactive anti-multipath efforts exerted in such designs in order to mitigate the fading and other undesired artifacts of radio frequency interference (RFI), the indoor wireless channels could still remain prone to fading and may exhibit poor RF link performance (specified in terms of bit error rates)4,5 due to reflection, scattering, shadowing, diffusion and diffraction suffered by the microwave energy, resulting in random attenuation and fading conditions on signal transmissions. Further, the current trends in indoor wireless applications involve using a grossly increased number of communicating hosts of collocated systems with multiple applications and standards.6–9 This is evident when considering such applications laid on industrial floors.4,5
Aimed at anti-fading mitigation efforts within such an environment, this article presents a new diversity method, based on “polarization-sense” antenna diversity, using a pair of right-handed and left-handed circularly-polarized (RHCP and LHCP) antennas located at each end of the RF link. The efficacy of a prototype is experimentally demonstrated along with simulated results.
Triumphs on Bit Error: Mitigation Methods
To mitigate the effects of EM-channel specific undesirable influences on RF link performance of indoor wireless communications, some of the strategies used in practice include: using adaptive transmitter power control; deploying polarization diversity on frequency-hopped transmissions; implementing antenna diversity on the transmitter side; and using adaptive frequency-hopping technique.
In spite of these approaches being considered and traditionally applied, when the host population in a given indoor premise grows, and in order to achieve a robust performance for such dense wireless networking (which are conceived mostly on an ad hoc basis), it has become necessary to study yet more options and alternative approaches that are more comprehensive, yield even better performance and are practically more tangible than those listed above. The diversity concepts, adopted to realize RF links with anti-fading characteristics in indoor wireless applications, are based on achieving a pragmatic power-to-performance trade off. They can be designed for dynamic diversity of operations. In other words, the diversity transmission can be implemented, as and when needed, consistent with performance requirements. Specific to indoor applications, for example, the use of spatially-separated antenna diversity has been described by Moon and Kim,12 where the diversity scheme is applied to WLAN transmissions (IEEE 802.11a and b). The method addressed is confined to receive diversity that makes use of two antennas at the receiver.
Another article by Beklas, et al.13 describes the application of a transmitter diversity concept for Bluetooth communications. It refers to the method of adaptively deploying an optimum antenna configuration in the transmit mode based on a decision taken on the signal characteristics (received signal strength indicator, RSSI) during the guard-time interval specified for Bluetooth links. Both antennas are located at the same site of the transmitter with the diversity applied to the antenna matrix governing two orthogonally-directed antenna beams. In other words, the relevant scheme is essentially a polarization diversity version of spatial diversity. It selects the optimum polarization (vertical or horizontal) using the RSSI data as needed (based on decision-controller information sent from the receiver).
The use of polarization diversity in Bluetooth transmissions had been originally suggested by Neelakanta and Sivaraks,6 who presented a method of applying switched-polarizations to frequency-hopped packets. Unlike the method of Beklas, et al.,13 their suggestion requires no RSSI-based decision to be applied in the diversity scheme. It is a simpler scheme devoid of a decision-logic controller. The beam-steering between the orthogonal set of antennas is done automatically on alternate or randomly-picked packets. It is entirely a hardware strategy at the transmitter that requires no increase in power budget.
The concept of using an orthogonal set of linear polarizations (VP and HP) in order to achieve polarization diversity can be extended for use in hybrid strategies where diversity is improvised both at the transmit and receive sides so as to augment the diversity gain of the RF link. The tax on having such multiple diversities (via the hybrid set) can, however, be kept low by optimizing the system complexity and eliminating the burden on the power budget.
Polarization-sense Antenna Diversity
Instead of using linearly polarized antennas, Kajiwara14 shows that circular polarization (CP) would help reduce multipath-fading effects more significantly. He has shown that the fade level could be marginally reduced by 7 to 11 dB with CP antennas (relative to linear polarization). As such, the associated transreception performance is expected to show better polarization performance. Further, the delay-spread can be reduced by approximately one-half its value.
In order to realize the anti-fade merits of using CP antennas and implement the diversity thereof, a way of making use of two circularly-polarized antennas (one excited in right-handed (RHCP) sense and the other in left-handed (LHCP) sense is indicated. These antennas can be kept physically close enough (to meet the space constraints); at the same time, however, they can be electrically isolated with minimal spatial correlation realized as a result of their opposing senses of polarization. That is, the present method follows a new concept of a viable polarization-sense antenna diversity scheme. Implementation of such RHCP and LHCP antennas in a hybrid (transmit and receive) diversity scheme is illustrated in Figure 1, where a pair of CP antennas (A and B) are kept closely placed at the transmitter-end and a similar pair (A' and B') is used at the receiver side. Further, the opposite sense of circular polarization is excited at each antenna of the pair; that is, A is RHCP and B is LHCP. Wi and Wj represent hopped sets of frequencies supporting the packets in a typical FHSS transmission.
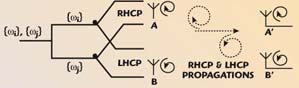
Fig. 1 Hybrid diversity scheme using polarization-sense diversity.
Pursuant to this scheme, the power-splitting between the colocated dual CP antennas A and B at the transmitter is illustrated in Figure 2. The antennas are simultaneously excited (each with 50 percent of the total power, P) yielding oppositely-sensed (RHCP and LHCP) EM waves. These waves are designated as ERC(t) and ELC(t), respectively. Some part of these transmissions at (fractional) powers of (1 – a) x (0.5P) and (1 – b) x (0.5P) are assumed to exist, which constitute the multipath waves experiencing (multiple) reflections as displayed.

Fig. 2 Proposed polarization-sense diversity scheme using dual CP antennas at the transmitter and receiver sites.
The oppositely-sensed CP components of the EM wave, ERC and ELC, can be expressed in terms of their associated linear orthogonal parts, EH(t) and EV(t), where the subscripts H and V designate the horizontal and vertical dispositions of the EM wave components. The phase difference between these linear components leading to circular polarization is π/2 radians. Hence, it follows that ERC = EH(t) + jEV(t) and ELC = EH(t) – jEV(t). Corresponding to the transmission scenario, the RHCP and LHCP components of the EM field at the receiver can be written respectively as

where the subscript set (k,ℓ) depicts the kth signal received after experiencing ℓ reflections and τk,ℓ are the associated propagation delays involved. Further, the first terms of Equations 1a and 1b correspond to single rays that prevail directly across the transreceive path as line-of-sight (LoS) transmissions, each experiencing a propagation delay of τ. The summation terms are contributions from multiple reflections whose coefficients are respectively denoted by ρk,ℓ:RC and ρk,ℓ:LC for RHCP and LHCP waves. Explicitly, ρk,ℓ:RC = [(|ρH:k,ℓ|)ℓ + (–|ρV:k,ℓ|)ℓ] and ρk,ℓ:LC = [(|ρV:k,ℓ|)ℓ + (–|ρH:k,ℓ|)ℓ], with ρV and ρH being the complex reflection coefficients for the orthogonal linear V and H components of the EM field obliquely incident on the reflecting surfaces. The associated phasors of these multiple reflections are responsible for fading effects at the receiver and it is shown here that such effects can be minimized by the proposed strategy.
A signal-summing process at an incoherent receiver delivers an output equal to the vector sum of rRC and rLC. Following this simple (incoherent) detection, the received signal-power to noise-power ratio (S/N)RX that can be realized is expressed as

with Ak,ℓ = [(|ρH|2)ℓ – (|ρV|2)ℓ x [1 – (–1)ℓ] and Bk,ℓ = [a – (–1)ℓb] x (|ρH|2)ℓ – [b – (–1)ℓ a] x (|ρV|2)ℓ; and, (S/No)LoS refers to the signal-to-noise ratio (SNR) when only a direct LoS condition prevails (without any multiple reflections).
Denoting the ratio (S/No)RX/(S/No)LoS as s, ideally, Equation 2 would reduce to s = 1 or (S/No)Rx ≡ (S/No)LoS, if |ρH| ≡ |ρV|, meaning that the magnitudes of the reflection coefficients of the horizontal and vertical polarization components are equal. However, this may not always happen in practice. As such, some residual multipath effects will invariably be present to some extent; the SNR of the system will approach that of a LoS link, however, if mutual cancellation of multiple-reflected H and V components is forced or emphasized. The present strategy enables such cancellation by virtue of the polarization-sense antenna diversity involved as could be evinced from the following simulated and experimental results.
Simulated Results
Figure 3 shows the simulated results (using MatLab™) of the SNR performance of the transreceive system compared to that of a direct (LoS) condition (devoid of multipath propagations). These plots depicting the value of s are obtained via the algorithm of Equation 2 by performing 10,000 iterations of computations. In each iteration, uniformly-distributed independent random values between 0 to 1 attributed to a, b, |ρH| and |ρV| are used. Further, a random number is presumed to depict the value of k; another random number is used to denote the multiple reflections (ℓ = 1 to 3, for example). Each iteration of computation depicts a time-slot of transmission. Figure 4 is a plot of the mean values of s, namely, s= E[(S/No)RX/(S/No)LoS] across the ensemble of iterations performed with ℓ = 1 to 10.

Fig. 3 Simulated results of S vs. iterations depicting transmissions; (a) dual CP antennas and (b) a single CP antenna.

Fig. 4 Mean value of S of the ensemble of iterations vs. the number of reflections l for dual CP antennas and a single CP antenna.
It can be observed that, for an ensemble of several iterations (that is, for a statistically large number of time-slots of transmissions), the range of mean values of SNR relative to LoS condition for the dual CP antenna system under discussion is about 84 to 78 percent, whereas the range for a single CP antenna system (Kajiwara) is about 36 to 40 percent.
Further, using this data, the bit error rate (BER = Pb) versus bit-energy to noise-power ratio (Eb/No) for a Gaussian frequency shift keying (GFSK) transmission across a Rayleigh channel (presumed to exist between the transmitter and the receiver) is computed for three cases: a straight LoS link with no multipath effects; an RF link with a single CP antenna system from Kajiwara; and an RF link with the proposed dual CP (RHCP and LHCP) antenna system. The resulting curves of BER versus Eb/No for the three cases indicated are plotted in Figure 5. A GFSK modulation is assumed to exist in all the simulations performed (as it would conform to Bluetooth transmission, for example). Furthermore, in all the simulations, an additive white gaussian noise (AWGN) is introduced with a power level consistent with the SNR value adopted in the simulations.
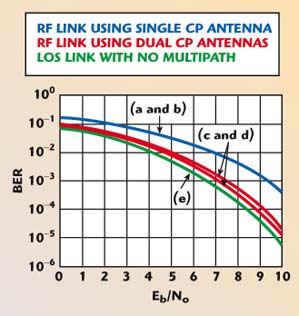
Fig. 5 BER vs. Eb/No.
Experimental Studies
The efficacy in deploying polarization-sense antenna diversity is further evaluated from experimental studies in an indoor range using a set of fabricated RHCP/LHCP antenna hardware. The transmitter and receiver side antenna pairs were designed using Archimedean spiral antennas excited by the aperture of pyramidal horns, as indicated in Appendix A.
The indoor-range experiment was performed at X-band (10 GHz), a set up available in the laboratory. While indoor wireless systems in the present study normally operate at 2.45 and/or 5 GHz, the antenna and microwave plumbing were appropriately scaled-down for 10 GHz operation meeting the availability of the laboratory facility. However, the diversity performance data so gathered and evaluated at 10 GHz can be extended to a lower frequency without any loss of generality.
The CP antennas constructed on PCBs correspond to RHCP/LHCP Archimedean spirals. The use of such CP antennas for compactness has been indicated by Ronglin and Guangzheng.15 These antennas, designed and adopted for the present experiment, are depicted in Figure 6.

Fig. 6 LHCP and RHCP test antennas with dimensions designed to fit the exciting horn’s aperture.
The measurement procedure consisted of three steps. First, only two pairs of standard horn antennas (linear polarization) were used at the transmit- and receive-sites. The signal levels (X1) at the receiver detectors (of left and right channels) were recorded (as reference levels). The second step involved the four antennas used (two at the transmitter and two at the receiver) corresponding to the RHCP configuration. The corresponding signal levels (X2) at the receiver (relative to step 1) were measured. In the last step, the transmitter side was fitted with RHCP antennas and LHCP antennas were mounted on the receiver side. Because of polarization sense discrimination, a reduction in received power was noted. The corresponding signal level at the receiver was X3. Hence, the polarization discrimination ratio (PDR) or polarization loss-factor (PLF) is given by 10 log 10 [(PRHCP/RHCP = X2)/(PRHCP/LHCP = X3)]. The oscilloscope traces of the measured levels of X1, X2 and X3 are shown in Figure 7. The measured polarization discrimination ratio (on repeated measurements) ranges between 4.5 and 5.0 dB.

Fig. 7 Measured demodulated signal waveforms (1 kHz) at the receiver.
Realizing the Polarization-sense Antenna Diversity Scheme: Practical Problems and Solutions
The method of using polarization-sense (PS) antenna diversity indicates a superior link performance. The plausibility of its implementation is demonstrated by the measurements yielding a data set on PDR. The PS antenna diversity is found to be compatible with implementation across a given work environment so as to yield minimal cross-interference through polarization discrimination. However, what can be expected as possible design problems and implementation concerns with the proposed follows:
1. The antenna diversity scheme calls for using two sets of circularly polarized antennas kept spatially separated. But just how far should they be physically separated? Considering the type of hosts in indoor applications (especially as in the sensor-based RF end-units), these antennas must be small and physically close enough, but at the same time should provide adequate diversity gain.
2. Any physical proximity of such antennas may cause mutual (impedance) coupling between them when adopted in small-sized transreceivers where such antennas (like patch antennas) may have a common substrate. Such geometrical and material considerations in realizing closely proximal antennas with minimum mutual impedance consideration need a careful design strategy.
With reference to Problem 1, the solution is to obtain an optimum spatial separation and at the same time achieve a desirable diversity gain. It is suggested in a recent study by Kar and Wahid16 that a low correlation can still be achieved if the orthogonal polarization antennas are of ±45° slant-types and are separated by just 0.2λ or more. At 2.45 GHz, this amounts to a physical separation of about one inch, which is reasonable for practical applications. In the strategy of using dual CP antennas, a relevant geometry can be configured in a style similar to the system suggested by Kar and Wahid.16
Problem 2 is concerned with mutual (impedance) coupling that has to be minimized whenever the antennas are closely placed. That is, collocation of dual CP antennas may cause mutual impedance problems, for which the counter-measures that can be considered include using Yablonovich structures17–20 or adopting superstrate dielectric covering (coating)21 of the patch antennas. The Yablonovich concept enables improvising an EM structure with a surface impedance compatible for isolation of units (such as antennas) that can be formed on such surfaces. These EM structures are conceived analogous to so-called photonic bandgap (PBG) crystals.
Concerning superstrate covering of the patch antennas, it is reported21 that a common dielectric cover on a system of patch elements can be optimized to control the mutual coupling between the elements in terms of relevant impedance relations between them. However, application of this concept has to be carefully reviewed while advocating it for circular-polarization antennas, considering the associated cross-polarization, purity of polarization, etc.
Details as reported on Yablonovich structures and superstrate-based patch antennas show that by optimal design of geometry and appropriate choice of materials, mutual coupling between proximal antennas can be reduced to a desired extent. A variety of patch antennas and planar inverted F antenna (PIFA) structures that have emerged in recent times can be duly considered and modified accordingly for the applications under discussion. For example, the dual CP antennas, as needed for polarization-sense diversity, can be conceived by using two equilateral triangle patch antennas as indicated by Suzuki.22 By appropriately locating the excitation probes on the patches, Suzuki has shown that it is possible to realize RHCP or LHCP radiation at a given frequency of operation.
Apart from Suzuki’s version of CP antennas, there are also other aperture-coupled patch configurations using separate feeds, which can be considered for dual CP excitations. In such structures, quarter-wave lines (instead of a branch-line coupler) can be used at the excitation geometry so that unwanted coupling between dual excitations is avoided. Cross-slot and etched-bar antennas are typical examples of such dual CP antenna structures that can be adopted for the proposed diversity scheme (instead of Suzuki’s structure).
Typically, as shown in Figure 8, a center-grounded circular disk/patch driven from the back via two probes located 90° apart is a viable CP antenna configuration. Alternatively, a square radiator with its two adjacent sides driven by a 90° hybrid can also be used.24

Fig. 8 Circularly polarized patch antennas; (a) circular patch and (b) square patch.
Yet another method towards realizing RHCP/LHCP excitations comes from Weinschel,23 who suggests using a single-fed CP antenna with a patch having deliberately introduced projections and notches. That is, single-fed CP antennas with appropriate perturbations on circular or square types of patches can be designed to excite RHCP/LHCP radiations.
A practical method of switchable RHCP/LHCP polarization can be designed with a basic structure of rectangular patch antenna excited by a diagonal slot fed by a microstrip line.24 This is illustrated in Figure 9, where PIN diodes introduced in the slots enable steering of the signal to right-handed or left-handed polarization. The electronics associated with these PIN diodes can be designed appropriately for the steering of the packets as required.6,7

Fig. 9 Circularly polarized patch antenna with sense switchable feasibility.
Adequate LHCP/RHCP segregation and significant cross-polarization isolation can be improvised with the composite structure shown in Figure 10. It has a lower feed-layer and an upper patch-layer. A single microstrip line excites two orthogonal coupling slots (by virtue of l/4 slot separation) so that RHCP or LHCP radiation is realized (depending on the port excited).

Fig. 10 Aperture-coupled patched antenna with separate feeds to yield RHCP and LHCP radiation.
In conceiving a dual polarization capability, regardless of the type of antenna geometry previously identified, the associated design should conform to appropriate size and symmetry of excitation elements (such as the slots), and RHCP/LHCP isolation limits and purity of polarizations.
More details on compatible designs can be seen in the references given by Neelakanta and Chatterjee,25 and Kossel, et al.26
Conclusion
The dual CP antenna system described here can successfully provide a polarization-sense antenna diversity enabling cancellation of reflected multipath components in RF transmissions for indoor wireless communications. Hence, this strategy would reduce the fading that may arise so that the corresponding receiver SNR can approach the strong LoS signal conditions.
Simulations pertinent to the present method and the corresponding experimental results obtained show tangible RF link performance improvement under multipath-fading conditions. The existence of conceivable dual CP antennas with possible decoupling methods (even when the antennas used are in close proximity) encourages the feasible aspects of the proposed method. Further, the practical considerations on implementation of the present system are illustrated by the experimental studies performed with the necessary hardware.
Further, multiple diversity can also be overlaid on the proposed technique. For example, the dual CP antennas of the proposed method can be alternated in supporting frequency-hopped (consequent) packets (excited at {ωi} and {ωj} sets of frequencies). This provides frequency diversity in addition to the polarization-sense antenna diversity realized by the opposing polarization senses of the CP antenna pair. The frequency-hopped packets generated in the traditional CDMA/FHSS efforts can be switched alternatively or applied randomly (as specified by a Bernoulli process) between RHCP and LHCP antennas. This is similar to the procedure indicated by Neelakanta and Sivaraks6 except that polarization sense diversity replaced the orthogonal diversity of HP and VP antennas. This method of superimposing frequency diversity would offer additional guard against fading as a result of implicitly achieving an additional diversity gain. Typically, such randomly-switched packets on LHCP/RHCP transmissions pertinent to CDMA/FHSS can provide a maximum of 3 dB additional improvement to signal-to-interference (SIR) ratio. Lastly, without any loss of generality, the proposed methods can be adopted as a hybrid mode of diversity improvised at transmit and receive locales.
References
- T. Grewe and S.A. Mujtaba, “Diverse Roads Lie Ahead for WLANs,” Wireless Systems Design, Vol. 8, No. 8, October 2003, pp. 28–31.
- M. McLean, “How to Design a Wireless LAN,” Communication News, Vol. 40, No. 9, September 2003, pp. 34–35.
- S. Selby, “Co-existence Warrants a Second Glance,” Wireless Systems Design, Vol. 8, No. 8, October 2003, pp. 36–39.
- P.S. Neelakanta and H. Dighe, “Robust Factory Wireless Communications: A Performance Appraisal of the Bluetooth™ and the ZigBee™ Colocated on an Industrial Floor,” Proceedings of the 29th Annual Conference on the IEEE Industrial Electronics Society (IECON03), Roanoke, VA, 2003, pp. 2371–2376.
- T.B. Tang, et al., “Toward a Miniature Wireless Integrated Multisensor Microsystem for Industrial and Biomedical Applications,” IEEE Sensors Journal, Vol. 2, No. 6, December 2002, pp. 628–635.
- P.S. Neelakanta and J. Sivaraks, “A Novel Method to Mitigate Microwave-oven Dictated EMI on Bluetooth Communications,” Microwave Journal, Vol. 44, No. 7, July 2001, pp. 70–88.
- P.S. Neelakanta, J. Sivaraks and C. Thammakoranonta, “Bluetooth-enabled Microwave Ovens for EMI Compatibility,” Microwave Journal, Vol. 43, No. 1, January 2001, pp. 138–151.
- P. Callahan and R. Durand, “WLAN Products Retain Stability and Control,” Wireless Systems Design, Vol. 8, No. 8, October 2003, pp. 32–35.
- S.M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communications,” IEEE Journal on Select Areas in Communications, Vol. 16, No. 8, October 1998, pp. 1451–1458.
- N. Flaherty, “Wi-Fi Heads for the Home,” IEE Communications Engineer, Vol. 1, No. 4, August/September 2003, pp. 10–13.
- A. Soltanian and R.E. Van Dyck, “Performance of the Bluetooth System in Fading Dispersive Channels and Interference,” Proceedings of the IEEE Globecom, San Antonio, TX, 2001, pp. 3499–3503.
- J. Moon and Y. Kim, “Antenna Diversity Strengthens Wireless LANs,” Communication Systems Design, January 2003, pp. 15–22.
- F Bektas, et al., “Bluetooth Communications Employing Antenna Diversity,” Proceedings of the 8th IEEE International Symposium on Computers and Communication (ISCC 2003), Kiris-Kemer, Turkey, 2003, pp. 652–657.
- A. Kajiwara, “Circular Polarization Diversity with Passive Reflectors in Indoor Radio Channels,” IEEE Transactions on Vehicular Technology, Vol. 49, No. 3, May 2000, pp. 778–782.
- L. Ronglin and N. Guangzheng, “Numerical Analysis of 4-arm Archimedian Printed Spiral Antenna,” IEEE Transactions on Magnetics, Vol. 33, No. 2, February 1997, pp. 1512–1515.
- M. Kar and P. Wahid, “Diversity Antennas for Wireless Communications,” Proceedings of the 7th World Multiconference Systemics, Cybernetics and Informatics, Orlando, FL, July 27–30, 2003, Vol. XI, pp. 9–12.
- E.Yablonovich, “High Impedance Ground Planes for Conformal Antennas,” http://www.ucop.edu/research/micro/abstracts/99_127.html.
- K.C. Huie, “Microstrip Antennas: Broadband Radiation Patterns Using Photonic Crystral Substrates,” MS Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, January 2002.
- F. Yang and Y. Rahmat-Samii, “A Low Profile Circularly Polarized Curl Antenna on an Electromagnetic Bandgap (EBG) Surface,” Microwave and Optical Technology Letters, Vol. 31, No. 4, November 2001, pp. 264–267.
- G. Poilasne, “Antennas on High Impedance Ground Planes: On the Importance of the Antenna Isolation,” Proceedings of the Progress in Electromagnetics Research Symposium, October 2003, pp. 237–255.
- K.C. Gupta and Benalla (Eds), Microstrip Antenna Design, Artech House Inc., Norwood, MA 1988, Chapter 10.
- Y. Suzuki, N. Miyano and T. Chiba, “Circularly Polarized Radiation from Singly-fed Equilateral-triangular Microstrip Antenna,” IEE Proceedings, Vol. 134, Pt. H, No. 2, April 1987, pp. 194–198.
- H.D. Weinschel, “A Cylindrical Array of Circularly Polarized Microstrip Antennas,” IEEE Antenna and Propagation International Symposium Digest, 1975, pp. 177–180.
- M. Boti, et al., “Circularly Polarised Antenna with Switchable Polarisation Sense,” Electronics Letters, Vol. 36, No. 18, August 2000, pp. 1518–1519.
- P.S. Neelakanta and R. Chatterjee, Antennas for Information Super Skyways: An Exposition on Outdoor and Indoor Wireless Antennas, Research Studies Press, UK 2003.
- M. Kossel, H. Benedicter and W. Bachtold, “Circular Polarized Aperture Coupled Patch Antennas for RFID System in the 2.4 GHz ISM Band,” Proceedings of the 1999 IEEE Radio Wireless Conference, pp. 235–238.

