The direct transponding of RF signals onto optical fiber is an important element in the implementation of efficient radio-over-fiber systems. MQW lasers exhibit transfer functions from RF to light, which generally offer good linearity, but adequate dynamic range for applications in cellular and cordless systems requires further improvement in this linearity parameter. Because the laser output is in a different medium from the input, techniques such as feed-forward are difficult to implement and predistortion is the favored approach.1–3 In order to optimize the predistorter characteristics, a description of its nonlinear behavior must be obtained in a form compatible with that of the laser. Since Volterra models of MQW lasers have been developed elsewhere,4 a similar model for the predistorter is required. Volterra series representation is sufficiently general to accommodate nonlinearity with memory in both the laser and the predistorter.
This article describes the derivation of a Volterra series representation of the nonlinear elements of the predistorter circuit, that is two Schottky diodes connected back to back. This configuration would ideally ensure the generation of only odd-order harmonics and intermodulation. A nonlinear model was constructed for the chosen diode by performing a series of measurements of DC I-V, capacitance-versus-voltage and conductance-versus-voltage characteristics. The accuracy of the model was then tested against practical measurements, using the harmonic balance test bench in the HP-CDS system. The values of the nonlinear elements shown in Appendix A were then extracted using the power series method. From the values of the capacitances and conductances, the Volterra series was then used to predict the level of the third-order intermodulation and its variation with input power level and operating frequencies.
Method Summary
The third-order distorter (nonlinear element) block is the only nonlinear block considered for the analysis, the remaining circuitry being assumed linear over the band of concern. The distorter used two type HP (HSMS-8202) diodes. The procedure of generating the third-order intermodulation distortion required for the linearization of the laser diode (type Ortel model 3540A-022 fiber optic transmitter) uses the diode equivalent circuit. The nodal equations for this circuit can be represented by the matrix equation at steady state
![]()
where

For identical diodes, g1 = g'1, g2 = –g'2, g3 = g'3, c1 = c'1, c2 = –c'2 and c3 = c'3, hence, Y1 = Y'1 gi and ci for i = 1 to 3 are the first three Taylor coefficients of the conductances and capacitors of the diode, respectively. îk for k = 1 to 4 are the distortion current sources associated with each nonlinear element. Thus, the computation procedure of the third-order IM components can be performed using the methods described in 5,6.
Simulation and Results
The procedure was performed with a FORTRAN program. For the intermodulation distortion (IMD) calculations, two tones, arbitrary separated with different phase and magnitude, are considered. The values of the capacitor, Ci and Co, shown in the third nonlinear element circuit, are both set to 1 nF and are negligible. The linear circuit elements of the diode are assigned the following values: c1 = 0.08 pF, r1 = 6Ω, L1 = 1.3 nH and L2 = 1.0 nH. The operating point of the diodes without input signals are 0.1516 V and 11.8 µA. The nonlinear circuit elements of the diode were simplified into nonlinear equivalent capacitance and conductance. The first three Taylor series coefficients of the nonlinear capacitor and conductance are given in Appendix B.
Figure 1 presents the variation of the calculated and measured third-order IM outputs as a function of the input power level. The frequencies of the two input tones are set to 1.80 and 1.86 GHz. The results show good agreement when the input power level considered is less than –20 dBm. Departure of measured and predicted results above this power level reflect the limitations of the three-term Taylor series in regions of high nonlinearity. However, in the application described, input levels of approximately –25 dBm would be entirely satisfactory.
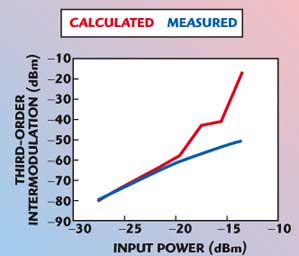
Fig. 1 Simulated and measured third-order intermodulation level vs. input power.
The calculated and measured third IM component levels as a function of the mobile frequency band are shown in Figure 2. The distance between the two input frequencies and the input power level are set to 2 MHz and –25 dBm, respectively. This result also shows that the frequency dependency caused by the nonlinear reactive elements is small.
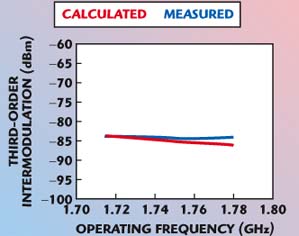
Fig. 2 Simulated and measured third-order intermodulation level vs. frequency.
The predistorter has been tried on an Ortel fiber optic laser, as shown in Figure 3.7 The specifications of the Ortel FP laser transmitter 3540A are: 1310 nm single mode, modulation bandwidth: 0.1 to 5 GHz; input third-order intercept point (IIP3) at 2 GHz: 30 dBm (33 dBm, typical); 1dB compression point: 13 dBm; equivalent input noise (EIN) at 2 GHz: –126 dBm/Hz (–130 dBm/Hz typical); relative intensity noise (RIN) at 2 GHz: –145 dBm/Hz (max); DC modulation gain (0.1 mW/mA) (0.16 mW/mA typical); optical power: 4 mW (7 mW typical); and input impedance: 50 Ω (SMA). The specifications of the Ortel PIN 2510B photodiode used are: 1310 or 1550 nm, bandwidth: 0.1 to 6 GHz; maximum optical input power: 2 mW; responsivity: 0.75 mA/mW; RF receiver efficiency: 50 percent at 6 dB RF loss; and output impedance: 50 Ω (SMA). Figures 4 and 5 show the measurements of IMD for two input tones on the Ortel laser, with and without the predistorter. As shown, the predistorter was able to compensate the third-order distortions over the DCS1800 frequency band.

Fig. 3 The DCS1800 optical transmission systems used to test the predistorter.

Fig. 4 Third-order intermodulation components for an Ortel laser without a predistorter.

Fig. 5 Third-order intermodulation components for an Ortel laser with a predistorter.
Conclusion
For an MQW laser operating in a quasi-linear mode, the weakly nonlinear characteristics of a linearizing predistorter are accurately modeled using a Volterra series. The method could readily be extended to include more significant nonlinear reactance for application to lasers exhibiting with-memory nonlinearity. The predistorter has been tried on an Ortel laser and was able to compensate for the third-order distortions occuring in the laser transmission over the DCS1800 frequency band.
Acknowledgment
Support by EPSRC under Grant Ref. GR/L10925 is gratefully acknowledged.
References
- H.T. Lin and Y.H. Kao, “A Predistortion Technique for Multichannel AM-VSB Lightwave CATV System,” Conference Proceeding on Lasers and Electro-optics, San Francisco, CA, 1995, pp. 367–368.
- P.G. Domingues and J.C. Pedro, “A New Predisortion Scheme for Reduction of Intermodulation Distortion in Optical Cable TV SCM Receivers,” Microwave and Optical Technology Letters, Vol. 7, No. 16, November 1994, pp. 769–776.
- K.Y. Lau and A. Yariv, “Intermodulation Distortion in a Directly Modulated Semiconductor Injection Laser,” Applied Physics Letters, Vol. 45, 1984, pp. 1034–1084.
- K. Liang, Q. Pan and J. Green, “Nonlinear Analysis of Quantum Well Lasers with the Effects of Carrier Transport,” IEEE Journal of Quantum Electronics, Vol. 35, No. 6, 1999, pp. 955–960.
- S.A. Mass, “Applying Volterra Series Analysis,” Microwave and RF, May 1999, pp. 55–64.
- H.M. Salgado, “Volterra Series Analysis of Distortion in Semiconductor Laser Diodes,” IEEE Proceedings, Vol. 138, No. 6, December 1991, pp. 379–382.
- Q. Pan and J.G. Gardiner, “Survey of Linearization Methods for DTI/EPSRC Link PCP Project: Radio Optical Broadband Integrated Network (ROBIN),” Internal Report 216/UB/0.1/TCN, July 1999.
