Both the IRIDIUM (LEO) and Odyssey (MEO) mobile satellite systems use constellations to provide worldwide continuous coverage. Each satellite in the constellation produces antenna beams covering wide areas. However, because the coverage areas are large, and the users in a coverage area may exceed the capacity of a single beam, the coverage is blanketed by multiple spot beams, which approximate a cellular structure on the ground. This, like in terrestrial cellular systems, permits frequency reuse, thus enhancing the capacity of the systems. Additional means are used to enhance capacity, of course, but this note will confine its attention to the cell topology only. The benefits accrued from using cellular partitioning with spot beams also result from the fact that the ground transceiver will see a higher effective isotropic radiated power (EIRP) emanating from the satellite and will see a higher G/T (receive antenna gain vs. noise temperature) when in its transmission mode.
The spot beams are generated by an on-board multi-beam antenna subsystem that lays down multiple spot beams approximating a cellular structure on the surface of the Earth. The multi-beam antenna design used by both Motorola and TRW use a two-dimensional Butler matrix beam-forming network to produce a pincushion footprint display within each coverage area.
The Butler matrix has been used extensively over the years in radar and electronic warfare (electronic support measures) and satellite systems.3 The Butler matrix consists of passive four-port hybrid power dividers and fixed phase shifters. It has N input ports and N output ports. As a beam-forming network, it is used to drive an array of N antenna elements. It can produce N orthogonally space beams overlapping at the –3.9 dB level, and having the full gain of the array. The network is most commonly used to produce volumetric beams in a pincushion deployment, where to be orthogonal sinX/X patterns must be spaced so that the cross-over is at about 4 dB down (2/π), and the sidelobes will be down 13.2 dB. Tapering will violate this requirement. For a cosine taper, for example, the cross-over level becomes approximately 9.5 dB for orthogonality.

Fig. 1 A two-beam Butler matrix.
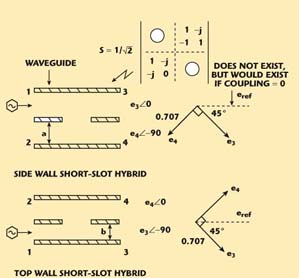
Fig. 2 Phase relationships in riblet short-slot hybrids, the basic building block of the Butler matrix.
A generic version of the Butler matrix used as a beam-forming network is shown in Figure 1. It consists of a 3 dB quadrature hybrid1 (see Figure 2 and Appendix A) driving two antenna elements with separation d. Note the amplitude and phase relationships for the hybrid structure.

For example, feeding the lower left-hand port of the coupler in the Butler matrix results in the antenna array being uniformly illuminated and differential phased to point the resulting beam peak to the right of boresight in direction O. With the phasing indicated, the relationship becomes
(2π d/λ) sinθ1 –π/2 = O
or sinθ = λ/4d
Feeding the lower right port 2 results in a beam pointing to the left of boresight at an angle θ2 = –λ/4d. If both ports one and two are driven, two beams will be produced at angles θ = ±λ/4d. The matrix produces N (equal 2 here) orthogonally spaced beams overlapping at the –3.9 level.
A slightly more detailed version producing four beams is shown in Appendix B. This consists of several quadrature hybrids and fixed phase shifters. It is noted that if one traces a phasor through the network, no boresight beam is formed and the beams are symmetrically deployed about the array axis. For the port driven in the figures it can be observed that the phase front across the aperture elements is –45°, –90°, –135° and –180°. Therefore, the shaded beam is produced.

The four-beam matrix may also have a sequencing switch on the input ports to scan to any one of the four positions shown. A more elaborate labyrinth can scan or produce many more beams.
In the basic array, the number of beams is equal to the number of elements, and the array factor is of the form sinNx/sinx, where N is the number of elements. Kraus10 has shown that the magnitude of the field intensity in the far field of a linear array of N istropic radiators is given by

where
E (θ) = element factor (weighs the array factor)
θ = (2 πd/λ) sinθ – δ
δ = progressive phase difference generated by the matrix and is equal to
δk = (2k – 1) π/N,
k = 1,2, ..., N/2
k = beam number
Note in the two-element array previously shown
δk = (2k-1) π/N
δ = π/N = π
The location of the beams can be found from the following relationship
sin θ = (π/Nd) [k–(1/2)]
The first sidelobe is down 13.5 dB, which is typical for a linear array with equal amplitudes and equal spacing. Interestingly, the beams cross over at the 3.9 dB points, which suggest that the beams are orthogonal and the network is lossless.
The sidelobes can be significantly improved by coherently combining two output ports to give a cosine variation with the sidelobes down by 23 dB, but with a beam distention of 35 percent. Figure 3 illustrates the addition of two beams each having uniform illumination (with sin x/x far field) to obtain a cosine illumination. In general, n+1 beams can be added to form a (consine)n illumination.

Fig. 3 Cosine illumination achieved by combining two adjacent beams.
There are other tricks that can be manifested by the matrix. The beams can be made to have limited scan by the use of the network shown in Figure 4. Power is varied to ports 3 and 4 (for example) and the variable power divider controls the power to each port. Varying the division of power steers the beam between individual beam axes.

Fig. 4 Beam scanning in a Butler matrix using a variable power divider.
Multiple volumetric beams can be generated by a Butler matrix by dividing the array into rows and columns. This is depicted in Figure 5. The columns consist of linear Butler matrices where the outputs of each column are the vertical number of beams. For this example, four beams are in each vertical stack. The outputs of the column matrices drive four row matrices. These are also Butler matrices. The outputs of the row matrix are used to produce four squinted vertical stacks. It is noted that prior to squinting, the column matrices produce vertical beam stacks (4 per stack) that are all pointing in the same direction.
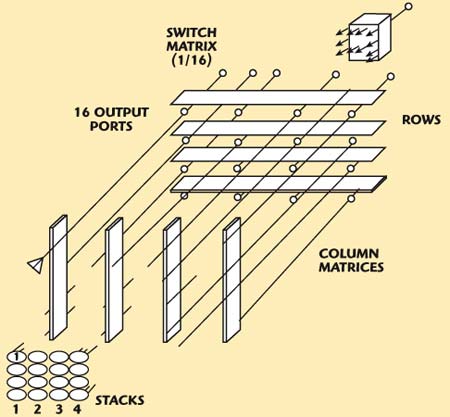
Fig. 5 A two-dimensional Butler matrix producing orthogonal beams.
For example, beam 1 is formed by column matrix 1, but is squinted upward from the horizontal boresight plane by the inherent operations of the matrix. The beam is now squinted to the left from the vertical boresight plane by the phasing of the row matrix 1 and its port 2. Correlating Appendix A with Figure 5 will help to make this clear.
There is a practical problem associated with the system shown in Figure 5. The stacked beam will form pencil beams only if the aperture size in the direction perpendicular to the column matrices is comparable to the array lengths. If there are horns with a cosine distribution, the aperture width in that direction would have to be equal to w = 69 λ/BW, where BW is the beamwidth in the vertical direction. The beamwidth in the vertical direction results from the array length. In the orthogonal direction, a very large flare may be required.
Generation of beams for volumetric coverage by a Butler matrix labyrinth requires considerable circuit complexity. Additional complexity results from circuitry to reduce the antenna beam sidelobe levels. With attendant low cross-over (9.5 dB for cosine taper and lower still for a smaller sidelobe level or high loss with a higher cross-over), the Butler matrix requires
H = (N/2) log 2 N
= (N/2) (log10 N/ log10 2)
= 3.32 (N/2) log10 N
quadrature couplers, plus fixed phase shifters. The number of fixed phase shifters is
P = (N/2)•
(log 2 N – 1)
For example, for a 64-beam system (8 x 8), 16 planar matrix feeds are required with 12 hybrid junctions and 16 fixed phasers for each matrix.
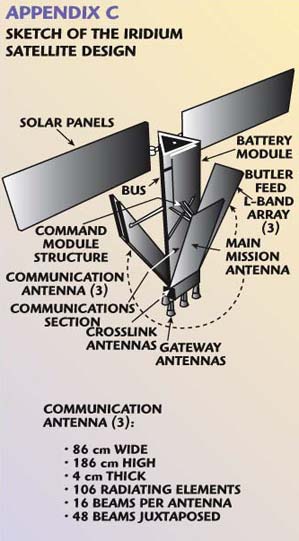
A sketch of the IRIDIUM spacecraft using the Butler matrix beam-forming network is shown in Appendix C. Each of the three communications signal arrays generate 16 spot beams. These beams are juxtaposed to produce 48 beams in the coverage area.
Conclusion
The Butler matrix is a versatile device. It can serve as a beam-forming network permitting volumetric beams to be generated that are orthogonal and independent, and each port will have the gain of the full array. Being passive and reciprocal, they can be used for both reception and transmission in an antenna array. The beams may be deployed simultaneously or sequentially depending on the application.
References
- H.J. Riblet, “The Short-slot Hybrid Junction,” Proc. IRE, February 1952.
- J. Butler and R. Lowe, “Beam-forming Matrix Simplifies Design of Electrically Scanned Antennas,” Electronic Design, April 1961.
- W.A. Sanders, “The Butler Matrix Transponder,” COMSAT Technical Review, Fall 1974.
- J.P. Shelton and K.S. Kelleher, “Multiple Beams from Linear Arrays,” IRE Transactions on Antennas and Propagation, March 1961.
- T. MacNamara, “Simplified Design Procedure for Butler Matrices Incorporating 90° and 180° Hybrids,” IEE Proc. H, Microwave and Antenna and Propagation, 1987, pp. 50–54.
- J.R.F. Guy, “Proposal for the Use of Reflected Signals Through a Single Butler Matrix to Produce Multiple Beams From a Circular Array Antenna,” Electronic Letters, 1985, pp. 209–211.
- R. Levy, “A High Power X-band Butler Matrix,” Microwave Journal, Vol. 11, No. 4, April 1968.
- R.C. Hansen, Microwave Scanning Antennas: Volume III, Academic Press, New York, NY.
- J.D. Kraus, Antennas, McGraw-Hill, New York, NY, 1950.
