This article focuses on a couple of key application areas for quantum technology in the aerospace and defense industry. In addition, it covers some of the measurement tools that are used in the development and analysis of performance for quantum-based systems. This article does not cover the physics of the quantum systems but refers to some of the key characteristics of quantum bits (qubits) as they are manipulated and measured (read the previous article in this supplement for the basics on quantum computing).
In general, the application of quantum technology in the aerospace and defense arena aligns well with the current adoption of quantum technologies in computing, sensing and communications. From an aerospace and defense perspective, one of the key application areas for quantum computing includes quantum key distribution (QKD) for encryption of sensitive data and prevention of cyberattacks. The extremely fast speeds of quantum computers for optimization of exponentially challenging algorithms enables them to also be used in the management of military missions and in deep space exploration.
The aerospace industry has for a long time taken advantage of the quantum effects for timing; an example is in the adoption of the cesium atom for precision timing. However, with the advent of the latest advances in the application of quantum mechanical behavior with newer atomic species, these structures offer more secure systems for positioning, navigation and timing.
Overall, quantum technologies are expected to provide several advantages that will include resilient and integrated communication systems and, in addition, open opportunities for precision navigation and timing. Also, providing the aerospace industry with the capability of having advance persistence, long range sensing systems.
CYBERSECURITY AND OPTIMIZED COMPUTATION
Today, cyberattacks can come from a variety of places and in a variety of forms. In Figure 1, two of the typical attackers and sources of cybersecurity threats are shown that include organized crime groups and foreign governments. Due to the potential processing power and sensitivity of quantum technologies, as well as the concept of quantum entanglement, it is expected that quantum computers will allow for the rapid development of highly encrypted communication systems using quantum cryptography. The currently safe and secure classical encryption has the potential of being broken using quantum computing technologies so governments are aggressively pursuing these new solutions.

Figure 1 Quantum key distribution enables encryption and security.
Quantum cryptography is the science of exploiting quantum properties to perform cryptographic tasks. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven to be impossible using only classical communication. The other area is the application of quantum optimization algorithms that could be used to speed up modeling of aircraft design for the ultimate performance.
Since the development of quantum computing technologies forms the basis for enabling the development of algorithms that offer robust methods of encryption and decryption in the aerospace industry, let’s start with a discussion on these solutions and how they may be applied, as well as how we may provide testing for these platforms. From a quantum mechanics perspective, the properties of “superposition state” and “quantum entanglement” form the basis for enabling the development of encryption and optimized computation algorithms. This implies that the quantum computers that are developed to address these needs would have to ensure that the quality of the qubits are based on providing high fidelity gates with low crosstalk.
In the physical realization of quantum computers, several technologies are used, including superconducting systems, trapped ion systems, spin qubits and neutral atoms. The cryogenic-based systems that operate in the millikelvin temperatures are typically superconducting and spin qubit systems. In some of the aerospace industry applications, trapped ion, superconducting qubits and neutral atom systems are more commonly adopted.
Superconducting qubits can consist of transmon qubits that require complex connection and cryogenic systems to perform operations on the qubit. Ion traps are slightly different and use atomic particles that are confined and suspended in free space using electromagnetic fields and are controlled using complex laser systems.
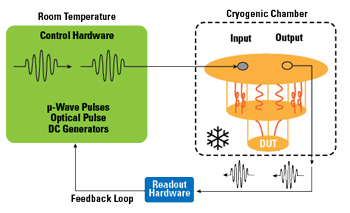
Figure 2 Simplified block diagram of a quantum computer.

Figure 3 Qubit control and readout hardware.
In order to understand the performance and measurement of these platforms, let’s look at the architecture of a typical quantum computer. From Figure 2, we see the key elements that make up the system include the control hardware for the qubits, the cryogenic chamber that includes the inputs and outputs, and the superconducting quantum computer chip itself. In general, the quantum computer is operated at cryogenic temperatures of ten millikelvin. The quantum computer control and readout are done using microwave pulses provided by control hardware.
The control hardware supplies signals to the system by means of microwave pulses, optical pulses and DC generators usually in the form of unique waveforms. Next, the quantum system requires a readout system that consists of making an excitation coupled with the quantum system. In many quantum error correction experiments, a feedback loop can be created between the control and readout hardware so that adjustments can be made to the control hardware.
Imperfections in the control hardware can affect qubit coherence times: jitter, phase noise, amplitude and temperature stability, noise and frequency accuracy. These problems are compounded as the number of qubits increases and the control system must deal with tens or hundreds of simultaneous control signals applied to these qubits.
To support these requirements, the control hardware that is typically used includes arbitrary waveform generators (AWG) and digitizers. For a quantum computing application, the AWG and digitizers must ensure high gate efficiencies, low latency, phase coherent time-dependent and sequential control pulses. In addition, the measurement and control hardware need to be extensible to allow for the control of several qubits as required in the computation as well as the seamless integration into the QKD distribution code and the cybersecurity algorithms.
This demands that the hardware is modular, allows for the lowest latency, provides excellent phase coherency and customizable software for the control of the quantum computer. In Figure 3, we see an example of the current PXI based AWG and digitizer solutions that has these capabilities.
The PXI AWG and digitizer platform shown in Figure 3 can be programmed at the hardware level using a hardware virtual interface and provides access to the FPGA’s used in the generation of the required waveforms. This addresses the need for low latency from control to readout and ensure ease of synchronization of the waveforms generated.
When utilizing quantum computers for any type of computation, it is important to know the resonance frequencies for each of the qubits that form part of the computer and how long your qubit will remain in a certain state. To characterize the qubit lifetime, Rabi oscillation experiments that help in the tuning of single qubit gates are used.
In Figure 4, we see a measurement of a qubit on an ideal resonance that was measured using a fast-triggered pulse sequence. The experiment involves driving the qubit between two energy states |0> to |1> and |1> to |0> repeatably. The Rabi experiment is such that a series of pulses of different amplitudes are applied to the qubit that is fixed on the resonance frequency.

Figure 4 Qubit resonance and decoherence.
Figure 4 also illustrates the on-resonance pi/2 condition that is determined by selecting an amplitude sweep that is half of what is used for the ideal on-resonance. As an example, the pi/2 pulse resembles the ideal qubit being manipulated from a |0> state into a superposition state |0> + |1>, which is in both the ground and excited state.
