A phase-locked loop (PLL) can be used for a range of purposes, including frequency synthesis. However, successful design of a synthesizer depends heavily on the choices the engineer makes, such as whether to employ a single or multiple loop approach, and on important design considerations like noise and spurious.
Understanding PLL Basics
In order to fully understand the choices and design considerations that come into play with the PLL, it is critical to first have an understanding of PLL basics. In the steady-state, a PLL is a linear control system where the variable of interest is phase. Laplace s-domain analysis is used to predict the stability and phase noise performance of the loop.
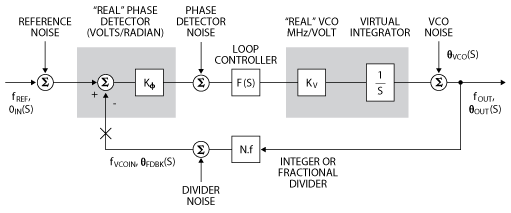
Figure 1 A basic PLL block diagram is illustrated here with the various noise sources.
A basic block diagram of a PLL is shown in Figure 1. The “input” to the PLL is the reference frequency and the output frequency is fOUT =N.f·fIN. With an integer divider, the output frequency steps are the same as the reference. With a fractional divider, the output step size can be much less than the reference. However, fractional dividers have serious spur issues and the phase noise is typically not as good as integer dividers.
The open loop transfer function is the gain around the loop, GH(s). Analyzing GH(s) gives the stability information about the loop expressed as phase margin. The reference, phase detector and N divider noise obeys a lowpass transfer function where the loop rejects the noise beyond the loop bandwidth (BW). The voltage-controlled oscillator (VCO) noise obeys a highpass transfer function where the VCO noise is rejected inside the loop BW. The loop controller F(s) is typically an integrator with a zero, although more complicated networks can be used.
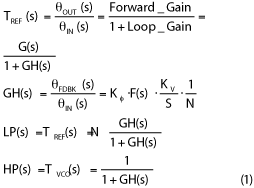
To model the noise associated with the various PLL components, the following equations can be used:
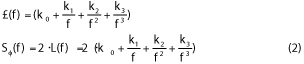
Here, L(f) is the single-sideband (SSB) phase noise at a given offset from the carrier and SΦ(f) is the double-sideband phase noise or power spectral density. The coefficients (k0, k1, k2, k3) represent the noise floor 10 dB/decade, 20 dB/decade and 30 dB/decade regions. Lesson’s model predicts that RF and µW oscillators have flat, 1/f2 and 1/f3 regions, while high Q oscillators (crystal and SAW) have flat, 1/f and 1/f3 regions. Dividers and phase detectors have a flat and 1/f or flicker region. For example, for a µW VCO, knowing the floor, a point in the 1/f2 region (dBf2_VCO, f2_VCO) and a point in the 1/f3 region (dBf3_VCO, f3_VCO), the noise equation is obtained.

The input noise sources are then multiplied by N to produce what is commonly known as the pedestal. The optimum loop BW is where the pedestal crosses the VCO noise. The total noise is the sum of the loop modified pedestal noise (low passed) and VCO noise (high passed). Taking 10 log of the output noise, less 3 dB, gives the final SSB noise.
The Single-Loop Approach
Single-loop phase-locked loops can be economical and efficient synthesizer solutions, offering a combination of moderate performance, compact size and low-power operation. Using commercial components such as fractional-N ASICs and careful modeling, they can be optimized to provide signals with reasonable phase noise, spurious performance and fine frequency resolution.
The Multi-Loop Approach
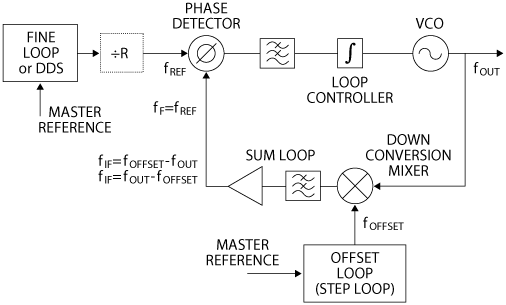
Figure 2 Shown here is a common multiple-loop synthesizer configuration. Note that the loop to generate the master reference is not shown.
The single-loop approach, however well optimized, has its limits. For higher performance synthesizers, multiple PLLs are used because they provide much better phase noise and spurs compared to simple, single-loop fractional N (FN) synthesizers. There are many configurations of multiple-loop synthesizers, one of which is depicted in Figure 2. It consists of a sum loop, fine loop and step loop.
The offset or step loop generates coarse frequency steps, while the fine loop (or DDS) generates a low-frequency, octave-wide signal with fine resolution that fills in between the coarse steps. The sum loop adds these two signals together. In general, the noise of the offset loop and master reference sets the “close-in” performance and the sum loop VCO sets the “far-out” performance. The fine loop should be a second-order contributor. Since the sum loop has a mixer, care must be taken with the frequency plan to avoid any spurs crossing within the loop BW.
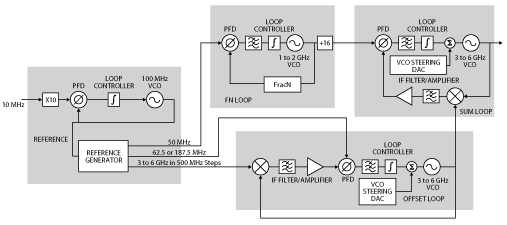
Figure 3 This block diagram graphically depicts the triple-loop approach employed in the N5181B and N5182B X-Series signal generators.
This triple-loop approach is used in the Agilent N5181B/N5182B X-Series Signal Generator (see Figure 3). The fractional N loop generates 62.5 to 125 MHz. The 3 to 6 GHz output of the offset loop (125 MHz steps) is mixed with the sum loop VCO output frequency to produce an intermediate frequency (IF) that is the same as the FN loop generated reference. By using upper and lower sideband mixing, full coverage is obtained.
The reference block generates a very low noise 100 MHz that is locked to a high quality 10 MHz reference. From this 100 MHz, the 50 MHz reference for the FN loop is generated. For the offset loop, a series of frequencies from 3 to 6 GHz is generated in 500 MHz steps. Two additional reference frequencies of 62.5 and 187.5 MHz are generated for the offset loop.
Offset Loop
The frequencies in the offset loop are all integrally related to n *500 MHz. Therefore, even though there is a mixer in the loop, there are no crossing spurs and the closest spur to the carrier is 62.5 MHz. VCO steering is necessary so the loop locks on the appropriate sideband.
The close-in phase noise of the offset loop is the sum of the n*500 MHz noise, 62.5 or 187.5 MHz reference noise, and phase frequency detector noise. This assumes perfect multiplication of the 100 MHz VCXO signal to 500 MHz and then up to the various harmonics. A fudge factor is added to take into account any extra noise sources.
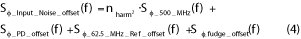
The 3 to 6 GHz VCO has rather poor phase noise. Consequently, the offset loop needs a wide-loop bandwidth to reject or track out the noise of the VCO. The offset loop controller consists of a differential lowpass filter, a low-noise differential to single-ended instrumentation amplifier, step attenuators to control the loop gain with changing KV. Each of these blocks, including the VCO tune port, adds phase shift in the loop that can adversely affect the phase margin and hence, the stability of the loop.
The differential lowpass filter rejects the 62.5 MHz energy from the phase detector so sidebands are not produced on the offset loop carrier. These sidebands can interact in the sum loop to produce a close-in spur on the final output. The trade off in designing this filter is to maximize the attenuation at 62.5 MHz while keeping the phase shift low at gain crossover. Within the passband of the filter, the phase shift can be approximated by a constant time delay.

Figure 4 The Bode and noise plots show excellent agreement between the model and measured results. The phase margin is ~48°.
The op-amp and VCO blocks are modeled with a simple time delay, T. The “lead lag” summing network was specifically designed to have flat attenuation with frequency. The gain crossover and open loop transfer function, assuming a delay of 24 nS, is shown in Figure 4 and given by:

Using the lowpass and highpass loop transfer functions, and the various noise source equations, the offset loop noise can be calculated using:
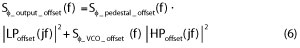
The phase detector, reference and other noise sources in the loop degrade the multiplied reference noise by about 5 dB, total. The loop bandwidth is set at ~3.2 MHz. This causes a large phase noise peak, which is attenuated by the sum loop. The offset loop noise is shown in Figure 4.
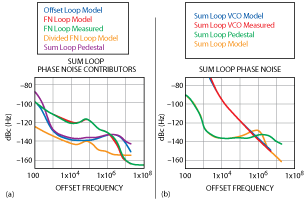
Fig. 5 The plotted results of the sum loop noise contributors and final output noise.
Fractional N and Sum Loop
The FN loop generates a 1 to 2 GHz output that is divided by 16 to produce the 62.5 to 125 MHz reference input to the sum loop. The FN loop uses an Agilent proprietary chip set with a 50 MHz reference, making the noise and spurious performance much better than commercially available parts.
Because of the division, the noise and spurs
in the FN loop are reduced by 24 dB before
the sum loop. The same methodology
is used to analyze this loop. The 1 to 2 GHz output
is divided by 16 to produce the 62.5 to 125 MHz
before the input to the sum loop. The divided fractional spurs are less than -90 dBc.
The sum loop uses a low-noise 0.75 to 1.5 GHz VCO that is multiplied to 3 to 6 GHz. The reference
input to the sum loop is the divided fractional N loop. The offset loop is summed using a mixer in
he feedback path. Since the IF frequency of the sum loop (mixer output) is much less than the offset loop (mixer input), the mixer crossing spurs are high order and hence, at a very low level. The noise of the sum loop, as shown in Figure 5, is given by:
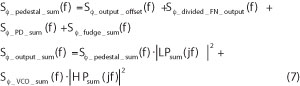
Using this mathematical software, it is easy to adjust the various loop parameters, such as gain crossover, pole and zero locations, and the various noise sources in the loop to optimize performance by performing “what if” scenarios. Once this is done, the component values can be calculated and a circuit simulator used, like Agilent’s Advanced Design System or SPICE, to verify each loop’s performance with the component values in place.
Conclusion
Regardless of how well optimized a single-loop PLL is, there are still limitations. Multiple-loop solutions can substantially improve performance in terms of close-in and wide offset noise, along with spurious. Using the right design and modeling approaches, multi-loop PLLs can efficiently deliver the performance needed for demanding applications.
Eric Drucker is a senior engineer with Agilent’s Technology Leadership Organization, a central resource for advancing measurement technology. He has been with Agilent for 12 years, working on PLL synthesizers for RF and microwave products and has taught numerous courses/workshops on PLL design. Prior to joining HP/Agilent, he spent the first half of his career with Fluke Corp. and several start-ups in the Seattle, Wash. area. He received his MSEE from Stanford in 1974.
