The requirement for increased data rates in modern radio systems has led to higher order modulation schemes which, in turn, demand oscillators with lower phase noise. Meanwhile, manufacturers must also deliver low cost solutions covering many different frequency bands. These two criteria have generally been incompatible, since an improvement in phase noise usually occurs at the expense of tuning range. As a result, manufacturers frequently incorporate many different oscillator parts into their radio systems.
An oscillator that combines good phase noise performance with flexibility and wide tuning range is therefore highly desirable. The classic feedback oscillator lends itself to meeting these requirements,1 while an MMIC-based implementation results in a low cost solution incorporating ancillary circuits such as buffer amplifiers, a prescaler and a frequency doubler.
Theory of Operation
Figure 1 is a diagram showing a simple feedback oscillator. This circuit will oscillate if there is a positive loop gain at a frequency where the open loop phase shift is a multiple of 2π. Oscillations will grow at that frequency until gain compression in the feedback amplifier reduces the loop gain to unity.
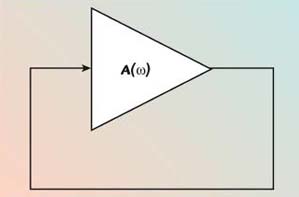
Fig. 1 Simple feedback oscillator
It is difficult to predetermine the oscillation frequency of the system accurately due to uncertainties in the loop phase shift. The insertion phase of the amplifier will vary according to manufacturing tolerances, temperature and supply voltage. In addition, at high frequencies, transitions and interconnects can significantly alter the loop delay. In order to cope with these uncertainties some means of phase control in the feedback path are incorporated to allow frequency tuning. Figure 2 shows the same simple feedback oscillator with a controllable phase shift in the feedback path.
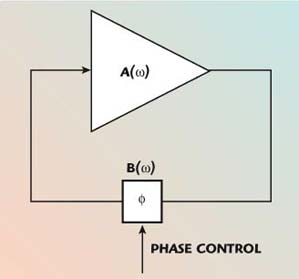
Fig. 2 Simple feedback oscillator with delay control.
If the amplifier is broadband, then there may be more than one frequency at which the oscillation criteria are satisfied, giving rise to unwanted oscillation modes and spurious output signals. To eliminate these unwanted oscillations, a filter can be placed in the feedback path. The filter reduces the open loop gain of the oscillator for signals outside the passband. It is generally chosen such that there is always just one frequency at which the oscillation conditions are met. Figure 3 shows the same feedback oscillator with a controllable phase shift in the feedback path and with the addition of a bandpass filter.
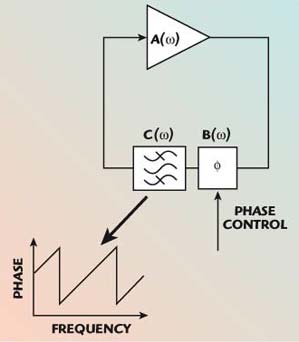
Fig. 3 Simple feedback oscillator with a filter in the feedback path.
The addition of the filter has a beneficial effect on the phase noise of the oscillator by increasing the slope of phase shift versus frequency. A larger phase versus frequency slope will cause the loop to be less susceptible to perturbations in phase. Various noise sources (principally thermal, shot and flicker noise) act on the loop phase and result in modulation of the output phase or frequency. The filter’s phase versus frequency response, or Q-factor, decreases the sensitivity of the oscillator loop to these noise sources and hence improves the resulting phase noise.
The Q-factor of the filter is typically much higher than the feedback amplifier, and increases with the number of stages in the filter. The phase noise in a feedback oscillator can be calculated according to2,3
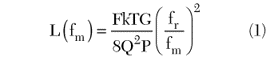
This expression demonstrates the importance of maximizing Q and the power in the loop P, while keeping the amplifier noise figure F to a minimum.
Circuit Implementation
One of the problems associated with feedback oscillators is the control of the loop phase. The amplifier, phase-shifter and filter must be designed to ensure that the loop phase is n•2π at the desired oscillation frequency. A versatile design that can be used with many different filters is difficult because the insertion phase of different filters will not be the same. There are also practical limits to the phase variation that can be achieved in a conventional phase-shifter; a large phase variation is undesirable due to the high oscillator voltage control coefficient (Kvco) it entails (this can be detrimental to phase noise and phase-locked loop (PLL) dynamics).
In this patented implementation4,5 the simple feedback oscillator approach has been extended by adding a four-quadrant vector modulator in the feedback path. This allows the designer to control the loop phase over a full 360°; hence, the same circuit can be used with many different feedback filters regardless of phase shift. In addition, the increased phase variation that is available increases the oscillator tuning range without resulting in an impractical Kvco.
Analog control of the vector modulator inputs is generally not practical so the I and Q control signals are generated in digital-to-analog converters (DAC) or digital potentiometers. An analog fine phase adjustment is incorporated to allow interpolation between vector modulator settings and to phase-lock the oscillator in a synthesizer.
In order to maximize the range of applications for this circuit, it has been designed to cover the widest possible bandwidth. In this case, acceptable circuit performance is achieved over one octave (6 to 12 GHz), and, with the on-chip frequency doubler, the circuit can be configured as a low phase noise signal source at any frequency between 6 and 24 GHz.
This novel feedback oscillator concept has been implemented in a commercial GaAs HBT process on a single highly integrated MMIC. HBT technology was chosen due to its combination of good RF performance at reasonable cost, and its low flicker (1/f) noise corner frequency compared to a HEMT processes. This is important since many modulation schemes require good phase noise performance at low frequency offsets such as 10 to 100 kHz. Figure 4 shows a diagram of the major circuit blocks inside the MMIC. The feedback filter may be implemented on-chip, or, for increased flexibility, a number of external filters may be used to address many different applications with the same circuit design.

Fig. 4 Block diagram of the feedback oscillator MMIC.
Feedback Filter
As shown, a filter is used to close the feedback path and determines the tuning range and phase noise of the oscillator. Thus far, the filter has been implemented both as a coupled-line structure and lumped-element filter on GaAs, but a variety of other technologies could be used, including:
• Dielectric resonator
• Microstrip on ceramic or soft substrate
• Waveguide
• Cavity
The choice of filter will determine the oscillation frequency, phase noise performance and tuning range of the system. The high performance and broad bandwidth of the oscillator MMIC allows the loop designer a great deal of freedom in optimizing these parameters through careful choice of both filter and operating point.
Coarse Phase Adjustment
A four-quadrant vector modulator is used to implement a coarse phase adjustment. This circuit allows 360° of adjustment. By providing 360° of phase rotation, the VCO can be made to oscillate at any point where the gain of the active circuit exceeds the insertion loss of the filter. This leads to a highly flexible architecture, since the absolute insertion phase of the filter at a desired oscillation frequency is not important.
The circuit is implemented as a pair of double-balanced Gilbert cell multipliers with frequency compensation. Balanced quadrature input signals are supplied by a Lange coupler followed by differential amplifiers. These circuits dominate the noise figure of the feedback circuit.
Figure 5 shows an example of how quantized phase adjustment over 360° of phase delay may be set using the vector modulator. For constant loop gain operation the vector modulator requires I and Q control signals that conform to cosine/sine functions. The magnitude of the I and Q signals can be adjusted to control the vector modulator gain, and thus optimize the loop gain to suit the chosen filter. Loop gain must be sufficient to ensure start-up, but not so large that gain compression degrades the phase noise performance.
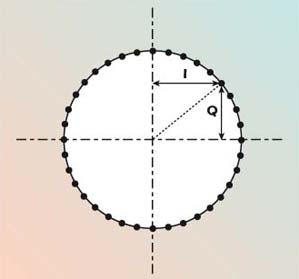
Fig. 5 Example of coarse phase delay settings.
Figure 6 shows plots of typical quantized phase delays from the vector modulator for three scaling factor settings. Small phase and amplitude errors (as seen in the slight non-circularity of these plots) arise due to the limited bandwidth of the quadrature Lange coupler and unavoidable asymmetries within the vector modulator.
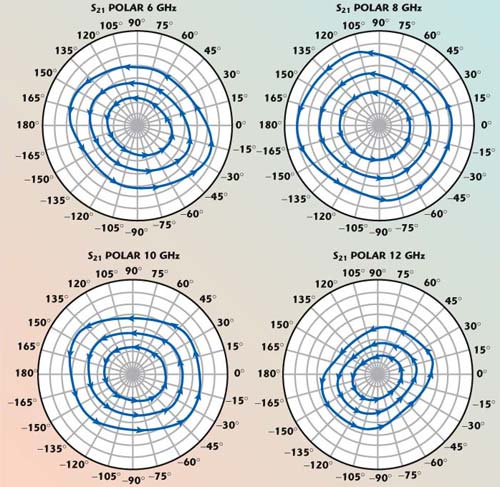
Fig. 6 Vector modulator phase characteristics at three scaling factor settings.
Fine Phase Adjustment
The fine phase adjustment is an analog input signal used to interpolate between coarse phase settings (see Figure 7) and allow phase-locking of the oscillator in a synthesizer. There are many ways of implementing the fine phase adjustment. The first implementation is shown in Figure 8 and uses a Lange coupler with controlled reflective terminations,6,7 in this case two arrays of varactor diodes. The insertion phase of the Lange coupler is controlled by varying the reactance presented by the diode terminations.
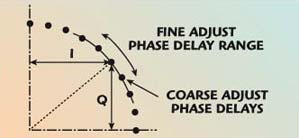
Fig. 7 Fine adjust phase delay range setting.
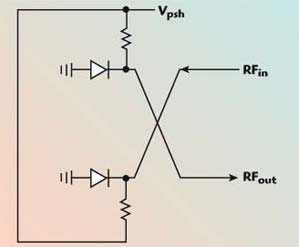
Fig. 8 Fine phase adjustment circuit.
A planned future implementation adds the analog control signal to the quantized I and Q control signals using a pair of two-quadrant multipliers to maintain the sense of analog control and removing the need for an extra phase shifter, thus improving the thermal noise figure and overall phase noise.
It is important that the fine phase adjustment range covers the widest gap that can occur between coarse phase adjustment points. This is necessary to avoid dead spots in the tuning range of the oscillator — points that can never be reached by the fine/coarse phase tuning.
The maximum phase variation in the fine phase adjustment will determine the minimum number of bits required to control the vector modulator. Some allowance must also be made for non-idealities in the vector modulator, manufacturing tolerances, temperature effects, etc. Figure 9 shows the tuning characteristics of the fine phase adjustment.
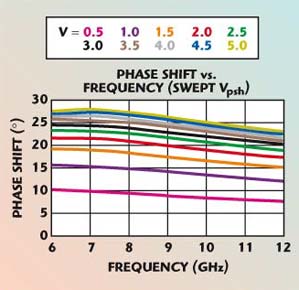
Fig. 9 Fine phase adjust characteristics.
Prescaler
To lock the feedback oscillator to a stable reference, a frequency divider is implemented on the MMIC and a port with the divided output frequency is provided. The divide ratio is 4 and the output power is approximately 0 dBm, allowing this circuit to interface directly to standard PLL ICs.
Doubler
The feedback oscillator MMIC also contains a frequency doubler circuit. The circuit is thus capable of generating output signals over two full octaves.
Synthesized Feedback Oscillator Implementation
Figure 10 shows a block diagram of a synthesized oscillator using the feedback oscillator MMIC. The microcontroller programs the PLL IC and sets the coarse phase adjustment according to sine/cosine lookup tables. If the PLL is out of lock and the desired output frequency is outside the range of the fine phase adjustment, then a window detector forces the coarse phase control to step through phase settings until lock is achieved.
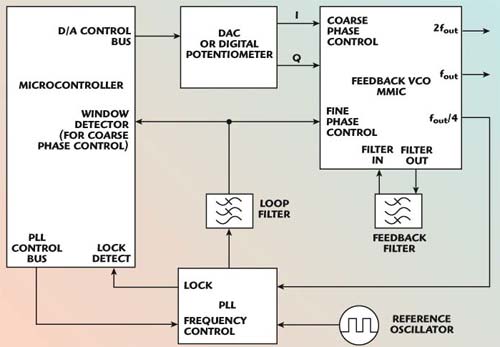
Fig. 10 Synthesized implementation.
The coarse phase control lines are low pass filtered with a cutoff frequency lower than the PLL loop bandwidth. In this way phase-lock can be maintained as coarse phase stepping occurs as required to compensate for temperature changes or to change frequency.
Oscillator Measurements
The circuit has been evaluated using three different filters with different bandwidths and circuit structures:
• A 7 GHz coaxial resonator filter with a 40 MHz bandwidth
• A 7 GHz coupled-line filter on GaAs substrate with an 800 MHz bandwidth
• A 7 GHz lumped-element filter on a GaAs substrate using metal-insulator-metal (MIM) capacitors and microstrip inductors with a 3 GHz bandwidth
The sharpness of the phase-delay versus frequency characteristic of the filter sets the phase noise of the oscillator. This characteristic can be traded-off with the filter bandwidth, which sets the tuning range of the oscillator. Figure 11 shows the measured phase noise of the MMIC implementation using the three filters previously described. A straight line extrapolation has been used to determine the anticipated phase noise with other filter bandwidths.
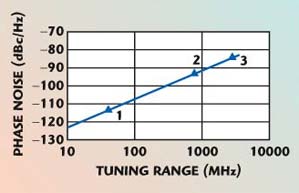
Fig. 11 Phase noise (at 100 kHz offset) vs. tuning range, using an external three-section filter.
The measured phase noise versus frequency offset for this circuit using the coupled-line filter (with > 800 MHz tuning range) is shown in Figure 12 for a carrier frequency of 6.672 GHz. The circuit has been phase-locked using the on-chip prescaler and a commercial synthesizer IC with a loop bandwidth of 5 kHz. The phase noise slope is 20 dB per decade above 100 kHz, indicating that flicker noise does not contribute to phase noise at offsets > 100 kHz.
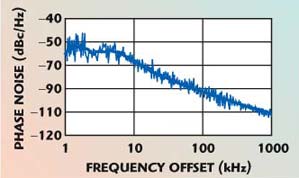
Fig. 12 Measured phase noise of feedback oscillator with 7 GHz coupled-line filter (800 MHz tuning range).
The octave bandwidth of the feedback VCO MMIC means that a very wide tuning range is possible. Measurements were made with a 3 GHz bandwidth lumped-element filter centered at 7 GHz. The filter response is shown in Figure 13 and the resulting tuning characteristic in Figure 14. The tuning range exceeds 40 percent while the buffered output power is +7 to +10 dBm. Future versions of this MMIC will improve the output power flatness.
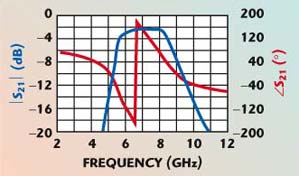
Fig. 13 Measured response of 3 GHz bandwidth filter.
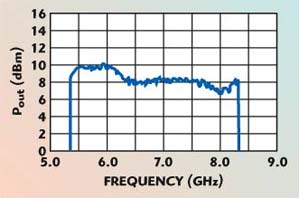
Fig. 14 Measured tuning range and output power of the feedback VCO with 3 GHz bandwidth filter.
Conclusion
Feedback oscillators are known to offer a good combination of low phase noise and wide tuning range; however, limited phase shift control can make the circuit inflexible. Designers have often been reluctant to use this architecture due to difficulties in predicting the loop phase shift with sufficient accuracy. The feedback oscillator has been shown to be highly suitable for a MMIC implementation, and, when combined with a vector modulator in the feedback path, the result is a highly versatile oscillator circuit.
Integration of the oscillator with a prescaler allows this circuit to interface directly with commercial synthesizer ICs, while a frequency doubler extends the potential output signal range to cover two octaves.
References
- J.T. Harvey and A.C. Young, “A Novel MMIC High Frequency Oscillator,” presented at MTT 2002 iMAPS sessions and available at www.mimixbroadband.com/AppNotes.html.
- D.B. Leeson, “A Simple Model of Feedback Oscillator Noise Spectrum,” Proceeding of the IEEE, Vol. 54, February 1966, pp. 329–330.
- J.K.A. Everard and K.K.M. Cheng, “Novel Low Noise ‘Fabry-Perot’ Transmission Line Oscillator,” Electronic Letters, Vol. 25, No. 17, 17th August 1989, pp. 1106–1108.
- US Patent No. US-2004-0012452-A1, “Frequency Adjustable Oscillator and Methods of Operation.”
- Australian Patent No. PCT/AU01/00997, “Frequency Adjustable Oscillator and Methods of Operation.”
- I.D. Robertson (Ed.), MMIC Design, I.E.E. London, 1995.
- S. Lucyszyn and I.D. Robertson, “Analog Reflection Topology Building Blocks for Adaptive Microwave Signal Processing Applications,” IEEE Transactions on Microwave Theory and Techniques, Vol. 43, No. 3, March 1995.
Patent information: Original – International Application No. PCT/AU01/00997 filed on 14 August 2001. US application was published on 22 January 2004 as publication number US-2004-0012452-A1. Japanese reference is 2002-520397 (13 Feb 2003). European application reference is 01957635.4.
