Modern electronics use time bases for a wide variety of applications. Communications systems rely on time bases for modulation and demodulation of data, GPS systems rely on them for accurate positioning, and a host of other applications rely on time bases to manage the flow of data within their system. As the range of applications grows and the frequency increases, designers need time bases that are tighter in stability and lower in noise. As a result, oscillator designers need to continually push the limit of tight stability, low noise design.
One of the major issues facing oscillator designers is the phase noise phenomenon. Phase noise is an undesirable entity that is present in all real world oscillators and signal generators. It can cause distortion or complete loss of incoming information in traditional receivers and high bit error rates in phase modulated applications. This makes it a necessity to quantify and understand this noise in the oscillator, so that its effect on the higher-level product is minimized.
Time is a concept all humans innately grasp as a function of life. It defines our world into days, months and years. When we look at a clock we know what time it is. However, do we really understand time and how it is defined? Like all measurements, time is measured with a degree of uncertainty. In engineering applications we use time bases that are by nature imperfect, adding uncertainties into the applications that are driven by them. A byproduct of this uncertainty is phase noise. The inherent instability present in every oscillator manifests itself as a spectrum of noise around the frequency of the oscillator. This noise band is generally measured from the carrier to 1 MHz away from the carrier. It is depicted as a graph of dBc/Hz vs. f(Hz), which shows how far down from the carrier power the noise power is at a given frequency in the following article. Many topics will be discussed, including:
• Different time bases and their properties
• Crystal oscillator properties
• Phase noise definition and calculations
• Ways to reduce phase noise in oscillator design
• Real oscillator phase noise plots
• Outside noise/interference effects on phase noise
The following information will show that phase noise is a manageable problem. Oscillator designers can work to minimize the phase noise in oscillators, and system designers using the oscillators can better design their systems and choose the correct oscillator for their needs. It is also clear that outside noise and interference degrades the phase noise performance of oscillators. Engineers need to be aware of these factors, so that their effects can be anticipated or avoided.
Time Bases
Engineers are used to looking at a frequency counter and reading the display to determine at what frequency an oscillator is operating at. But what is the accuracy of that measurement? The uncertainty of the measurement is dependant upon the accuracy of the time base the counter uses to drive its internal circuitry. This time base is not perfect and therefore skews the results of the frequency reading. For those applications requiring very precise frequency measurements, the accuracy of this time base is of the utmost importance.
Time, like every other measurement man has ever made, has an uncertainty. However, time is the most accurate standard that mankind has produced. The second is defined as the resonant frequency of cesium 133 (Cs-133), which is 9,192,631,770 Hz.8 Therefore, by measuring these vibrations of cesium, a standard for time is established. NIST (National Institute for Standards and Technology) is the keeper of the time standard for the United States. As of 2005, the NIST standard has an uncertainty of 5X10–16 s, which means it would neither gain nor lose a second in 60 million years.9 Cesium clocks, despite their accuracy, have several drawbacks making them unsuitable for mass usage in commercial electronics. The cost of cesium standards is prohibitive for using them as a time base. Secondly, they are large. The NIST standard fills a good portion of a room, and while smaller cesium standards are readily available they are not a portable item. The cesium standard due to its nature has a warm-up time; therefore, keeping power supplied to it is important, because a break in power could mean degradation in accuracy. Lastly, cesium standards use fuel; the cesium naturally depletes, rendering the device effectively ‘out of gas.’
Since cesium cannot effectively be used for commercial electronics or for most lab applications other timing sources must be considered. Rubidium offers extremely accurate frequency generation similar to cesium, although it suffers from the same pitfalls. Being only slightly less accurate than cesium, the rubidium standards have a high cost associated with them. They are not portable devices and must be in a fixed location. The rubidium standards also have the same depletion problem as cesium.
The choice for most consumer electronics is the quartz crystal oscillator. Quartz operates via the piezoelectric effect. Voltage applied to the crystal causes it to vibrate in a very stable and predictable way. A desired frequency of oscillation can be obtained by cutting and shaping the quartz. Quartz has many advantages. For example, it is inexpensive (compared to cesium and rubidium), it is small (crystals can be obtained in package sizes less than 3.2 x 2.5 mm) and has a high Q (> 500K for larger blanks). These traits have made quartz the industry choice for timing devices for many decades.
Quartz Crystal Oscillators
Crystal oscillators (XO) come in many types, shapes and sizes. XOs are comprised of a quartz crystal and driving circuitry. These bare bones clocks are inexpensive and small, but offer limited accuracy as the crystal will wander in frequency approximately ±30 ppm over temperature. Temperature-controlled crystal oscillators (TCXO) use a compensation voltage to correct for the crystal’s natural temperature drift. This is accomplished with a classic thermistor resistor network or a polynomial generator. TCXOs are tighter stability over temperature (±0.25 ppm can be obtained) and are small (2.0 x 2.5 mm is available) with low power consumption (2 mA in some cases). Microprocessor controlled crystal oscillators (MCXO) use a microprocessor to correct for the crystal’s natural temperature drift by sensing the temperature of operation and using that data to correct the frequency of the oscillator. These oscillators can achieve stabilities of ±0.1 ppm over temperature, but have a slightly larger footprint, consume more power and have degraded noise characteristics due to the microprocessor running in the oscillator. Oven-controlled crystal oscillators (OCXO) and double oven-controlled crystal oscillators (DOCXO) offer the greatest stability that quartz crystal oscillators have to offer. By heating the circuitry, the crystal stays at an almost constant temperature, nearly eliminating the natural temperature drift of the crystal. Stabilities of parts in 10-10 over temperature are achievable, but at the tradeoff of footprint (at least 1 inch square) and power consumption (possibly over 1A).
Despite having a high Q, the quartz crystal oscillator is not perfect. Ideally a sinusoidal oscillator would produce a voltage such that

where
Vo = amplitude
fo = frequency
t = time
However, real world oscillators have some amplitude fluctuations and phase fluctuations present within them and behave as in4

where
λ(t) = amplitude fluctuation
Φ(t) = phase fluctuation
The frequency of the oscillator is affected by several factors; temperature, long-term drift and short-term instability. Quartz is quite sensitive to temperature variations, and the frequency generally drifts between ±30 ppm over the temperature range of the crystal. Long-term drift, also called aging, is a natural phenomenon of the quartz and is well understood. The aging characteristic is defined as

where
t = time in days
A, B and fo = constants determined from least squares fit (as per MIL-PRF-55310D)7
Figure 1 shows the aging characteristic of quartz is a natural log function that slows over time. This means that the frequency drift of the oscillator will diminish as time passes. This is a desirable effect in terms of long-term performance. The oscillator will drift but that rate of change will slow and the oscillator in effect will become more stable.

Short-term stability or Allan variance (AVAR) is a measurement of the short-term frequency variations from the oscillator. Generally AVAR is specified relative to a particular gate time. For example, a 20 ms gate time may be selected and 100 samples taken and applied to the following formula:

where f(i)-f(i-l) is the difference between successive frequency measurements (as per MIL-PRF-55310D).7
The result provides an approximation for how stable the oscillator is reading-to-reading at the given gate time. By lengthening the gate time, the oscillator’s Allan variance decreases showing it is more stable over longer averaging periods.
Jitter
This measurement shows that the instantaneous frequency of the oscillator is not constant, but varies slightly about the nominal frequency creating an uncertainty in the frequency at any given point in time. This frequency change can be viewed as a change in time of the waveform edge from the ideal nominal frequency edge. This change in time of the edge is called jitter. Figure 21 illustrates the jitter effect on a square wave.

Jitter can be measured in the time domain and is expressed in a peak-to-peak time variation of the edge. However, this method may not be very useful in some applications because the variations in the edges are coming from the entire band of frequencies and exaggerating the magnitude of the jitter. Most real world applications will operate within a certain band of frequencies and therefore the jitter effect only needs to be measured in that band. To effectively see and measure jitter over a particular frequency band, conversion to the frequency domain must take place.
Phase noise
This conversion to the frequency domain results in a measurement called phase noise. It is expressed as a graph of power vs. frequency. To understand this measurement the jitter-to-phase noise conversion must be explored. One way to measure jitter is to measure the variance of each period from the average period, such that5
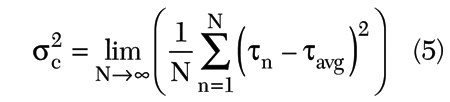
This RMS cycle jitter can then be used to calculate the phase noise at a given frequency, as

where
fosc = frequency of the oscillator
f = frequency offset from the carrier5
This computation can be done at many discrete frequencies and compiled into graphical form. Equations 5 and 6 assume that there is no l/f noise or burst noise.5 In real world oscillators these noise sources are present.
If real world components and the noise that is generated in real world circuits is taken into account the phase noise calculation gets more complex. The Leeson equation as shown below provides an estimation for how circuit noise and circuit elements factor into the phase noise measurement.6

where
Q = loaded Q of the circuit
fn = frequency from the carrier
fc = flicker noise corner frequency
fo = carrier (oscillator) frequency
T = temperature in Kelvins
Pavs = power through the resonator
F = noise factor of the active device
k = Boltzmann constant

Figure 3 shows how this equation fits into the plot of phase noise. It can be seen that close into the carrier, flicker noise dominates the curve and has a cut-off frequency of the corner frequency of the active device. The middle portion of the phase noise plot follows Leeson’s equation and is a combination of loaded Q, noise factor, power and temperature.6 For frequencies above fo/(2Ql), the floor is determined by noise factor, temperature and power.
From this plot it is fairly easy to come up with guidelines for minimizing phase noise in oscillator designs. Use devices with low flicker noise. Since the 9 dB/octave section is dominated by this quantity, reduction of circuit flicker noise is of great concern. BJTs have a much lower flicker noise than FETs making them more suitable for low phase noise applications. The 6 dB/octave section implies that a higher circuit Q is of great interest as is noise factor and power. OCXOs utilize crystals with higher Qs than TCXOs. Higher drive power is also desirable because that is the driving factor for the phase noise floor (frequencies above fo/(2Ql)). This comes with a tradeoff because higher drive levels usually result in some phase noise degradation close in to the carrier.

Phase Noise Measurement
Measuring phase noise is not an easy feat. Most spectrum analyzers do not have the resolution to measure the phase noise of a crystal oscillator directly. Figure 4 shows the normal configuration for phase noise testing. An ‘ideal’ source that is the same frequency as the oscillator under test is mixed against the oscillator. This produces the products of these two signals and also the difference. Using a low pass filter, the products are stripped away leaving only the difference, which will be the oscillator noise, if the ‘ideal’ source is exactly the same frequency as the oscillator.

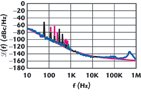
This resulting noise signal can then be measured by a spectrum analyzer and displayed as a graph of dBc/Hz vs. Hz. This graph is displaying in terms of power how far the noise (at each particular frequency) is below the carrier (oscillator’s desired signal). Figure 5 shows an OCXO (two-inch square package) plot that has a floor of around –170 dBc and a 10 Hz performance of approximately –130 dBc. Figure 6 depicts the phase noise performance of a 5 mm x 7 mm TCXO, which has a floor of around –155 dBc and a 10 Hz performance of approximately –90 dBc. Both plots are typical phase noise measurement plots.
OCXO phase noise performance is commonly much better than that of TCXOs. This is due to several factors. The OCXO is inherently more stable than the TCXO giving it improved phase noise performance. This is because the crystal in the OCXO is thermally stable where the TCXOs crystal is responding to the environmental changes. Even though there is compensation for those ambient temperature changes it is nowhere near as stable as the OCXO.

Secondly, OCXOs use different crystal cuts than TCXOs and as a result have a higher Q. A TCXOs crystal Q is approximately 30,000 to 40,000, where an SC-cut ovenized crystal may have a Q approaching 1,000,000. This higher Q directly improves phase noise in the oscillator. Lastly, TCXOs are designed to be much smaller and have very low power consumption. This means most of them are constructed using FETs instead of BJTs. FETs have a much higher inherent flicker noise, which worsens the phase noise characteristics of the oscillator. Ovenized units designed for stability use BJTs, which have lower noise specifications and in turn better phase noise performance.
Measurement Flaws
One of the issues with this measurement system is that the oscillator is mixing under test against an ‘ideal noise free’ oscillator. Since there is no such real world device the oscillator must be mixed under test against something known to be much better than the unit under test and assume that the ‘reference’ injects no noise. Another option is to mix it against something that is equivalent to the unit under test, and assume equal contribution from both oscillators. Both of these methods are inherently flawed. By mixing against something better one is assuming no degradation from the reference. If a reference that is 10 times better is available, the effects are minimal, but there is still degradation in the measurement.
By mixing against an equal source and assuming equal contribution, 3 dB is added to the target, which allows the operator to accept results that really exceed the intended specification because there is another noise source. However, how does one really know that they are equal? In fact, most times they are not equal. One source will have better noise characteristics than the other and this creates ambiguous data. Actually, if the unit picked as a ‘reference’ ends up being a relatively clean source and equal contribution is assumed, the operator could be accepting results that are in reality failing, but he or she has no way of knowing.
Outside Noise/Interference

Aside from the circuit characteristics, measurement assumptions and random crystal fluctuations, the oscillator and its phase noise behavior are affected greatly by the power supplied to the oscillator. Figure 7 shows a TCXO with a noisy power supply. Spurs can be seen between 80 and 1000 Hz with an amplitude of approximately –40 dBc. Figure 8 shows the same TCXO tested with a cleaner supply and only two spurs remain with amplitudes of approximately –20 dBc. The oscillator manufacturer has no control over what power supply the operator uses in their application and therefore just the oscillator’s phase noise performance is characterized and not the impact of the supply on the oscillator. As a result, the cleanest possible supplies are used for these measurements.
Nearby interference can also show up in phase noise measurements. Figure 9 shows the TCXO with a clean supply running it, but a computer monitor running about three feet away from the oscillator and test set. Figure 10 shows the same test with the monitor turned off. Again, the spurs appearing in Figure 9 are not from the oscillator and are therefore eliminated by shutting off the computer monitor during testing.

These real world plots show where the disconnect between consumer and manufacturer comes into play. Oscillator manufacturers attempt to characterize just the oscillator’s phase noise performance, and as a result go to great lengths to accomplish this. Clean power supplies or even batteries are used in an attempt to reduce the noise injected from the outside, reducing or eliminating any nearby interference such as computer monitors or other equipment running in the immediate area. Some manufacturers even build a Faraday cage, or shielded room to reduce outside interference. Many use baffles or buffers to reduce airflow around the oscillator making it more thermally stable.

What is wrong with that? The result of all of these efforts is an attempt to eliminate all outside interferences so just the oscillator’s performance can be measured. However, customers purchasing the oscillators may not realize that these great lengths were taken and the impact of the external effects. Secondly, the oscillator is not going to be running in a shielded room all by itself. It will be in a larger assembly with temperature gradients and non-ideal power supplies and probably other machinery or computers running nearby. Therefore, if a user looks at a phase noise plot and assumes this is what they have in their system there could be a substantial descrepancy. If no headroom is allowed for in their design, serious problems could occur.
Lastly, there are two other factors that directly affect the phase noise performance that the oscillator manufacturer has no control over. Vibration affects the phase noise of crystal oscillators, as described in the following formula:

where
Γ = oscillator’s g-sensitivity
A = amount of gs in the vibration
fo = frequency of the oscillator
fv = frequency of the vibration10
Most military designers are well aware of this degradation and work with the manufacturer to understand and characterize the oscillator under the vibration it will see in the field.
Another factor that hinders phase noise performance is multiplication. Many users will purchase an oscillator in the megahertz region and multiply it up into the gigahertz range. This is acceptable and will provide a stable oscillator but its phase noise is reduced by

where
N = factor of multiplication10
Vibration and multiplication are two processes that the user might be subjecting the oscillator to that the manufacturer would have no idea about and cannot give the user an indication about performance degradation. Therefore, if at all possible, it is important for designers to understand the affect these variables have on the time base and to work with the oscillator manufacturer so that the required quality of the timing device is appropriate for a particular application.
Conclusion
Phase noise is a very important aspect of any real world time base. From the previous discussion an oscillator designer can come to several key conclusions that will help minimize the phase noise in an oscillator design. Maximizing Q, using low noise active devices and increasing resonator power are the three main things to be done when reducing the phase noise in an oscillator. The oscillator designer can also see that the method of testing greatly affects the results of the test. Low noise supplies or batteries can be used to reduce phase noise from supply ripple. Nearby interference from computers, lighting, or other machinery should be eliminated. Finally, thermal buffers can be used to ensure that the test is only measuring the oscillator’s noise and not noise from outside entities.
Understanding the phase noise phenomenon and characterizing its effects are paramount to communication system design. From a user’s perspective this article should be helpful as a tool to understanding phase noise better and also understanding how it is tested and what factors outside of the oscillator will degrade its performance. There have been many instances where users did not specify what was required, or did not obtain the performance that they thought they were getting. This is a result of how the oscillator industry goes about performing the phase noise test. The attempt is made to eliminate any and all outside influences on the oscillator so that the oscillator’s noise characteristics can be assessed. This is legitimate and understandable, but the consumer of this product needs to be aware that the device will be used in less than ideal conditions and certainly more interference is present than was present when the phase noise was measured by the manufacturer.
As noted above, other factors in the end application can cause phase noise issues that the user did not anticipate such as vibration and multiplication of the signal. At the very least system designers should communicate with the oscillator manufacturer to let them know what is the likelihood of noise in their system so that the oscillator manufacturer can relate a more realistic picture of the phase noise performance of the oscillator that is being purchased.
References
1. N. Roberts, “Phase Noise and Jitter: A Primer for Digital Designers,” EE Design, July 14, 2003.
2. “Clock Jitter and Phase Noise Conversion,” Maxim Dallas Semiconductor, 2004.
3. S. Fry, “Quartz Crystal-based Low Phase Noise Oscillator Characteristics,” Greenray Industries Inc., 2005.
4. B. Kleinle, “Phase Noise in Crystal Oscillators,” Greenray Industries, 2004.
5. R. Poore, “Phase Noise and Jitter,” Agilent Technologies Inc., 2001.
6. “Phase Noise,” http://www.zen118213.zen.co.uk/Systems_And_Devices_Files/PhaseNoise.pdf.
7. Oscillator, Crystal Controlled General Specification For, MIL-PRF-55310D, 1998.
8. L.A. Breakiron, “Cesium Atoms at Work,” http://tycho.usno.navy.mil/cesium.html.
9. NIST-F1 Cesium Fountain Atomic Clock, http://tf.nist.gov/timefreq/cesium/fountain.htm.
10. J.R. Vig, “Quartz Crystal Resonators and Oscillators,” US Army Electronics Technology and Devices, Fort Monmouth, NJ, 1990.

John Esterline holds a BSEE degree and is currently pursuing his master’s of engineering in electrical engineering degree from Pennsylvania State University. He is currently an oscillator design engineer at Greenray Industries Inc. He has been involved in the testing and design of precision crystal oscillators for five years. He may be contacted via e-mail at jesterline@greenrayindustries.com.
