The vector signal analyzer (VSA) has several measurement advantages over a spectrum analyzer in the acquisition of bandpass RF signals, including its time-domain capture, which enables measurement of both magnitude and phase information, and its ability to display data in the time and frequency domains.1,2 The highly sampled, down-converted waveform gives a good amount of spectral detail around the carrier frequency. However, the resolution of the frequency spectrum may be affected by the relation between the length of the time capture and the bandpass signal envelope period for periodic signals such as multisines.3–5

A procedure for optimizing VSA measurements of periodic signals to minimize spectral leakage is presented. The underlying principle of this method has been known for years,5 but it finds new application with the recent emphasis on the use of periodic well-behaved signals to characterize complicated wireless devices, systems and channels. In these situations, multisine test signals, consisting of a collection of sine waves at frequencies that are slightly offset from each other to emulate digital test signals, are often used. In these test environments, complete knowledge of the stimulus is obtained and it becomes practical to use this type of measurement method. This procedure determines the proper settings such that the VSA will obtain an integer multiple of the envelope period of the measured signal, as illustrated in Figure 1. Specifying an integer multiple of periods preserves an undistorted time-domain signal. Thus, the FFT used by the VSA will portray the frequency-domain characteristics of the signal with minimal distortion as well. This method also negates the need for time-domain filtering (windowing) for periodic signals, which is one method for improving the spectrum when a fraction of an envelope period is present at the input.6 Eliminating filtering removes one more potential source of distortion in the measurement and is useful when looking for a weak adjacent tone or distortion product.

Vector Signal Analyzer Settings that Affect Spectral Leakage

FFT Considerations

The beauty of this procedure is in its simplicity. Although the VSA has many advanced features, such as filters, which ensure amplitude accuracy and help reduce side lobes on the acquired signals, as well as modulation/demodulation functions to interpret digital signals, this procedure uses only the RF signal and, after it is digitized, the FFT function of the VSA. The FFT is integral to the VSA for transforming the acquired time record to the frequency domain. It is an efficient algorithm for calculating the discrete Fourier transform (DFT) by significantly decreasing the quantity of calculations, from 2N2 to 2N log2(N), for N points in a sequence.7 The FFT algorithm essentially replicates the captured section of the time-domain signal applied to its input such that it is periodic for all time. For modulated RF signals, if the FFT input does not have an integer number of time-domain envelope cycles, there will be a discontinuity on the input to the FFT, which results in finite amounts of power being spread over multiple frequency bins in the spectrum, as shown in Figure 2. This spreading decays around a given spectral peak as 1/ƒn, where the degree n is related to the smoothness of the function in the time domain (that is n is higher for a smoother function than for one with sharp discontinuities). Superimposed on this decaying function is a sinc function, due to discretization and is called “spectral leakage.”4–6

VSA Settings

Four VSA parameters are considered to ensure the periodicity of the time-domain input to the FFT (called “self windowing”):6 the number of acquired frequency bins, the frequency span, the resolution bandwidth (RBW) and the acquired time window. Some VSAs use noise bandwidth (NBW) instead of RBW. RBW is defined by the hardware; NBW is defined mathematically. Otherwise, they perform the same function. Each parameter is described and then a method is developed for setting them to minimize the spectral leakage. This method may be applied directly or with minor modifications to many currently available commercial VSAs. The effect of these four parameters on the FFT in a VSA is demonstrated using a five-component multisine m(t), as shown mathematically in Equation 1. Although here these principles are applied to VSAs, they are true for any FFT calculations.

The first parameter considered is the number of frequency bins to use in the VSA measurement. The VSA takes a time-based measurement and then performs an FFT to produce the data necessary to find the signal spectrum. The FFT runs fastest if the actual number of recorded frequency bins is a power of two (such as, 64, 128…131,072).3,8,9

The number of frequency bins displayed on the analyzer usually does not equal the number of bins acquired. For the calculations shown here, one must use the actual number of bins acquired. The second parameter considered is the frequency span. The frequency span, the RBW and the time window are all interrelated and, for this method, a change in one parameter will force a change in one of the other parameters. First, an approximate value for the frequency span is chosen to ensure that the frequency band of interest will be captured in the measurement. However, the time window capture length and the RBW must still be taken into account before settling on the final frequency span that minimizes spectral leakage. The third parameter, the RBW, sets the spacing between frequency bins when no windowing is applied.10 In this case, RBW is the inverse of the time window, and is proportional to the span and inversely proportional to the number of frequency bins the VSA is set to calculate. The fourth parameter is the time window. This sets the time capture length, so the VSA obtains either an integer or fractional number of envelope periods for each acquired signal. Thus, the time window determines whether the signal acquired by the FFT is smoothly periodic or has discontinuities.

Five-component Multisine

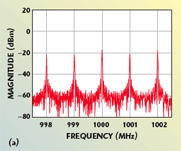
The test set-up is shown in Figure 3. First, a simple multisine is considered since it clearly shows the effects of the VSA parameter settings on the spectral leakage. A vector signal generator is used to create a five-component multisine, where the components have equal amplitudes and zero-degree relative phases. For the measurement examples shown here, the output power of the signal generator was –10 dBm; the frequency spacing between the tones (Δƒ) was 1 MHz and the center frequency was 1 GHz. A measurement of the signal generator output taken with non-optimized VSA settings is shown in Figure 4. The skirts around each tone demonstrate the spectral leakage referred to earlier. This spectral smearing can cause amplitude and phase error in the measurement, particularly for weak signal components. To make accurate measurements without windowing, it is essential that these five sine waves fall directly on five of the measurement window frequency bins after the FFT is performed. Figure 5 shows the result of this not happening for two of its five sine components. To eliminate spectral leakage and obtain a clean spectrum, the four key parameters mentioned above, frequency bins, frequency span, RBW and time window, must all interrelate properly. Since this procedure requires having maximum flexibility in setting these parameters, some adjustments must be made to the VSA’s default settings. First, the RBW coupling must be set such that the RBW can be changed independently from the span. Second, to have maximum flexibility in setting the RBW, the VSA must be able to allow a user-defined RBW to be specified (not all VSAs have this option). Third, all windowing filters must be disabled. For some VSAs, this corresponds to a brick wall filter. This allows the direct FFT result to be clearly seen. Fourth, the number of frequency bins is set. For the example shown, the maximum of 131,072 frequency bins was used, the highest setting for N to lower the spectral floor and show the most detail. For some VSAs, the setting one enters for frequency bins is 2N/1.28. The results shown used only 128 points.

The next step is to choose an approximate frequency span (Spanapprox) that will display the spectrum of interest. For this example, 5 MHz is chosen. Using Spanapprox and the number of frequency bins (N), the time window (TWapprox) is calculated to be 26.2144 ms using the relation

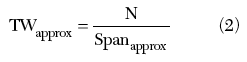
The time window must be equal to an integer number of the signal-envelope periods to avoid truncation errors caused by the periodic nature of the FFT. As a result, TWapprox needs to be refined. For multisines with equally spaced frequency components, the envelope period can be easily found by taking the inverse of the frequency spacing between adjacent sine waves (Δf) within the multisine that are being measured. This inverse is then multiplied by the largest value of M that will satisfy the equation

A high M ensures that an integer number of periods are acquired without the need for phase locking or triggering. Using Δf = 1 MHz, the integer M = 20,000 was found to give an optimized value of 6.5536 MHz for the span used:

This acquired span is equivalent to the displayed span of 5.12 MHz (or 6.5536/1.28) on the VSA used for the measurement shown previously. If the inverse of the optimum time window is taken, the RBW is obtained, and the VSA can now be set to these optimized Span/RBW/TW settings. It is important to specify as many digits as possible. The results are optimal when rounding is minimized for each setting. From the spectrums shown, note how the skirts around each sine wave have vanished. This clean spectrum indicates that the FFT has obtained a periodic input with no discontinuities. This corresponds to an integer number of envelope cycles in this case. Of the parameters discussed in eliminating spectral leakage, it is found that the span had the greatest impact on minimizing amplitude and phase errors for the multisine spectrum. It is, however, important to optimize all four parameters because measurements of small signals surrounding each sine wave could be distorted or obscured by spectral leakage.

Conclusion

A method has been described for reducing the spectral leakage when performing a spectrum measurement on a VSA. This method, based on acquiring an integer number of envelope periods of a bandpass signal, is general enough to be applied to most commercially available VSAs. Since the VSA takes a time-based measurement, it is important that the number of frequency bins, span, time window and resolution bandwidth are set such that the FFT calculation can be optimized. This provides a clean spectrum and may improve the measurement of the signal’s magnitude and phase and the resolution of small signals.

Acknowledgments

The authors wish to thank the following reviewers from industry, NIST and academia: Ken Voelker, product manager, Agilent Technologies; Abhay Samant, RF software group manager, National Instruments; Bill Byrom, application engineer, Tektronix; Kevin Thomason, application engineer, Rohde and Schwarz; Eric Hakanson, design engineer, Anritsu Co.; Andrew Dienstfrey, mathematician, NIST; and Dominique Schreurs, professor, Katholieke Universiteit in Leuven.

Note: Certain commercial equipment, instruments, or materials are identified in this article in order to adequately specify the experimental procedure. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.

References

1. “Modulation Analysis for Transient RF Signals,” Tektronix Technical Brief.

2. “Perform More Effective RF Measurements Using Vector Analysis,” National Instruments Application Note.

3. “The Fundamentals of Signal Analysis,” Agilent Application Note, AN 243.

4. E.O. Brigham, The Fast Fourier Transform and Its Applications, Prentice Hall, Englewood Cliffs, NJ, 1988.

5. R.G. Lyons, Understanding Digital Signal Processing, Second Edition, Prentice Hall, Upper Saddle River, NJ, 2004.

6. “Vector Signal Analysis Basics,” Agilent Application Note, AN 150-15.

7. http://mathworld.wolfram.com/FastFourierTransform.html.

8. J. Archambault and S. Surineni, “IEEE 802.11 Spectral Measurements Using Vector Signal Analyzers,” RF Design, June 2004, pp. 38–49.

9. “Time-Capture Capabilities of the Agilent 89400 Series Vector Signal Analyzers,” Agilent Product Note, PN 89400-10.

10. “Understanding Time and Frequency Domain Interactions in the Agilent 89400 Series Vector Signal Analyzers,” Agilent Product Note, PN 89400-12.