TECHNICAL FEATURE
A Ka-band Planar Printed Antipodal Linearly-tapered Slot Antenna
A Ka-band (27 to 32 GHz) planar antipodal linearly-tapered slot antenna (ALTSA) is designed, fabricated and measured. The numerical simulation was performed by 3D finite-element method (FEM). The printed ALTSA has been realized by using an RT/Duroid printed circuit board (PCB) substrate. The realized Ka-band ALTSA is characterized by broadband, high gain (approximately 14.5 dB at 30 GHz) and easy fabrication. The ALTSA could be a good choice in Ka-band local multipoint distributed systems (LMDS).
Meng-Chung Tsai
and Huey-Ru Chuang
Department of Electrical Engineering
National Cheng Kung University, Tainan, Taiwan, R.O.C
The rapid growth of the Internet has increased the demand of broadband services. In 1997, the FCC issued a second report and an order for spectrum allocation in the 28 GHz band for use in point to multipoint applications, which are typically referred to as local multipoint distribution service (LMDS). LMDS offers a wireless method of access to broadband interactive services. It combines telephone, video services, high speed data and emerging integrated media applications. The FCC has proposed two separate licenses. One, referred to as "Block A," is for 1150 MHz, which includes the spectra from 27.5 to 28.35 GHz, 29.10 to 29.25 GHz, and 31.075 to 31.225 GHz. The second license, referred to as "Block B," includes the spectra from 31.0 to 31.075 GHz and 31.225 to 31.3 GHz, for a total of 150 MHz. Conventionally, 30 GHz Ka-band LMDS antenna design use highly directional antennas, which are usually reflector antennas with diameters of over 10". It is of great interest to design broadband and high gain planar printed antenna for Ka-band communication applications.
The broadband and high gain nature of tapered slot antennas (TSA) have been reported for years. Due to its coplanar structure, the TSA is easily integrated with MICs. Some parameters that affect the performance of the TSA, such as the thickness of the dielectric substrates and the profile of the tapered slot, were presented by Yngvesson, et al.1 R. Janaswamy and D.H. Schaubert proposed a good stepped approximation to analyze the TSA with exponential taper profiles, which are the general cases of TSAs.2 Nevertheless, the conventional feeding technologies applied in TSAs, including coplanar waveguide (CPW)-to-slot transition, coaxial-to-slot transition, or even finline feeds, all face the difficult problem of impedance matching. To surmount the impedance matching difficulty, a TSA with antipodal geometry was introduced by E. Gazit.3 A so-called ALTSA that operates at K-band was reported by R.N. Simon, et al.4 One of the advantages of the antipodal geometry is that the designer does not need to layout any stubs on the PCB to achieve impedance matching.
In the past, the design of TSAs was usually based on empirical design rules. In addition, analysis methods presented were focused on coplanar structures, especially on TSAs with an exponentially tapered slot profile. 3D rigorous numerical modeling of the complete planar ALTSA structure had yet to be studied. In this article, a high frequency structure simulator (HFSS) based on 3D finite-element method (FEM) was employed to simulate a planar Ka-band ALTSA. A printed ALTSA has been realized using a RT/Duroid PCB substrate. The simulated results show that the designed ALTSA offers broadband impedance matching and high gain (more than 10 dBi) at 30 GHz. A 3D FEM simulation of the complete structure and the measured response of the realized ALTSA are compared to check the simulation accuracy.
ALTSA GEOMETRY DESCRIPTION
The geometry of a Ka-band (25 to 35 GHz) planar printed ALTSA is shown in Figure 1. The top metallization of the ALTSA starts from a feeding microstrip line and gradually flares with an angle 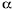 . The bottom metallization consists of a ground plane of the feeding microstrip and is also flared to the symmetrical side of the top metallization with the same angle
. The bottom metallization consists of a ground plane of the feeding microstrip and is also flared to the symmetrical side of the top metallization with the same angle 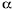 . The arcs with radius r1 on the top and bottom metallization are adjustable to make the microstrip line smoothly connected to the tapered slot antenna section without discontinuities. It can result in broadband impedance matching. As for the arcs with radius r2 on the bottom metallization, they can be arbitrarily chosen to make the feeding section changed from an unbalanced to a balanced structure. The feed structure is essentially a broadband balun. Referring to the previously published empirical design rules,5,6 the structure parameters are listed as follows:
. The arcs with radius r1 on the top and bottom metallization are adjustable to make the microstrip line smoothly connected to the tapered slot antenna section without discontinuities. It can result in broadband impedance matching. As for the arcs with radius r2 on the bottom metallization, they can be arbitrarily chosen to make the feeding section changed from an unbalanced to a balanced structure. The feed structure is essentially a broadband balun. Referring to the previously published empirical design rules,5,6 the structure parameters are listed as follows:
|
|
PCB Substrate: RT/Duroid 5880 (0.508 mm thickness,
εr = 2.2, tan* = 0.0009)
Antenna length: L = 43 mm
(about 4.3  at 30 GHz)
at 30 GHz)
Flare angle: 2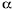 = 11°
= 11°
Feeding microstrip line:
length (LB + LM ) = 7 mm,
width w = 1 mm
Radii of the arcs: r1 = 7.75 mm,
r2 = 2 mm (r1 and r2 are adjustable to make the microstrip line smoothly connected to the ALTSA without any discontinuities)
3D FEM SIMULATION
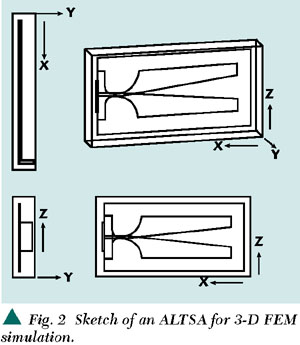
The high frequency structure simulator (HFSS) based on 3D FEM is employed to solve Maxwell's equation for the Ka-band ALTSA. Figure 2 shows the sketch of an ALTSA for 3D FEM simulation. Due to the design frequency of 30 GHz versus the 16.5 x 50 mm ALTSA dimensions, the total number of tetrahedrons in this finite-element modeling is 30,247 and the matrix size is 195,921. It is observed that, due to the geometry and the high frequency, a high number of FEM meshes is needed to accurately model the ALTSA structure and simulate the electromagnetic response. Figure 3 shows the 3D finite-element meshes used in modeling the ALTSA, and the 3D finite-element meshes used to model the whole structure of the ALTSA within an absorbing-boundary-condition
(ABC) box.
|
|
The total computing time is about 9 hours, including 18 iterations at 30 GHz, fast sweep over 50 frequency points and 10 frequency points ports-only solutions from 25 to 35 GHz. The computing platform is a Pentium-III 600 PC with 1GB RAM.
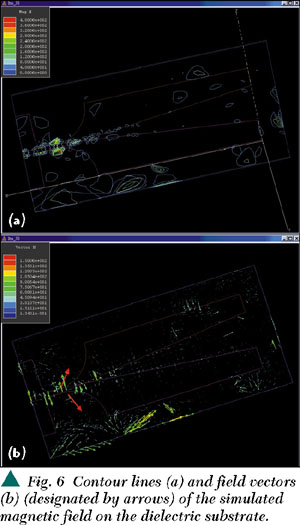
The simulation results indicate the distributions of the current, electric and magnetic fields, and 3D radiation patterns of an ALTSA. Figure 4 shows the visualization of the computed current distribution on the top and bottom metallizations of the ALTSA from 27 to 32 GHz. It can be observed that the electric current distribution concentrates mainly along the flared edges of the antenna and on the broadband balun. The gradually flared edges can be considered to accommodate a continuous change of wavelengths over a broad frequency range, which results in the broadband impedance matching performance. Since the wavelength at 30 GHz is about 1 cm and the length of the ALTSA metal-radiator is about 4 cm, approximately 8 cycles (including positive and negative phase cycles) of the current distribution along the flared edges of the radiator are observed. Figures 5 and 6 show the electric and magnetic fields, respectively. Clearly, the simulated radiation patterns, shown in Figure 7, illustrate that the E -component is the main contribution to the radiation pattern, and the E
-component is the main contribution to the radiation pattern, and the E -component contributes only to the cross-polarized component.
-component contributes only to the cross-polarized component.
|
|
COMPARISON
BETWEEN MEASUREMENTS
AND FEM SIMULATION
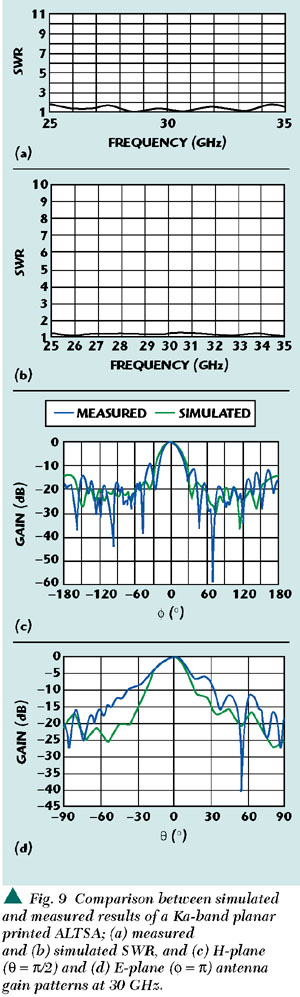
Figure 8 is a photograph of a realized planar printed ALTSA. The measured and simulated input SWRs are shown in Figure 9. Good agreement is achieved. It is also observed that the SWR is less than 1.5 from 27 to 32 GHz due to broadband characteristics. The antenna gain patterns in the H-plane and E-plane of the ALTSA are also shown. Satisfactory agreement is observed in the main-beam region. The computed directivity of the ALTSA at 30 GHz is 13.8 dBi compared with the measured value 14.6 dBi. Table 1 is a summary of the simulated and measured results.
|
|
CONCLUSION
The 3D finite-element method (FEM) design simulation, realization and measurement of a Ka-band (27 to 32 GHz) ALTSA antenna have been performed. The input SWR of the realized ALTSA on a RT/Duroid substrate is less than 1.6 (27 to 34 GHz). The antenna directivity is approximately 14.6 dBi at 30 GHz and the half power bandwidth (HPBW) is about 30° in the H-plane and 24° in the E-plane. The measured results show that the structure of the ALTSA perform in a multioctave bandwidth, with moderately high gain (with respect to general TSAs of about 7 to 10 dB gain), and symmetrical E- and H-plane gain patterns. The ALTSA could be a good choice in Ka-band wireless communication systems, such as LMDS, which have been commercially operated for short-distance and high data rate transmission services.
ACKNOWLEDGMENT
The authors would like to thank the Ansoft Corp. and Agilent Technologies for supporting the HFSS software. *
References
1. K. Sigfrid Yngvesson, Daniel H. Schaubert and Erik L. Kollberg, et al., "Endfire Tapered Slot Antennas on Dielectric Substrates," IEEE Transactions on Antennas and Propagation, Vol. AP-33, No. 12, December 1985, pp. 13921400.
2. Ramakrishna Janaswamy and Daniel H. Schaubert, "Analysis of the Tapered Slot Antenna," IEEE Transactions on Antennas and Propagation, Vol. AP-35, No. 9, September 1987, pp. 10581065.
3. E. Gazit, "Improved Design of the Vivaldi Antenna," IEE Proceedings, Part H, Vol. 135, No. 2, 1988, pp. 8992.
4. R.N. Simons, R.Q. Lee and T.D. Perl, "Non-planar Linearly Tapered Slot Antenna with Balanced Microstrip Feed," IEEE AP-S International Symposium, Vol. 4, Chicago IL, 1992, pp. 21092112.
5. K.S. Yngvesson, et al., "The Tapered Slot Antenna A New Integrated Element for Millimeter-wave Applications," IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-37, No. 2, February 1989, pp. 365374.
6. Chen Wu, Linping Shen, Gang-Yi Deng, Ying Shen and J. Litva, "Experimental Study of a Wide Band LTSA Which is Fed by an Inverted Microstrip Line (IML)," IEEE Antennas and Propagation Society International Symposium, Vol. 4, 1998,
pp. 23282331.
|
|
Adaptive Feedforward Amplifier Linearizer Using Analog Circuitry
Alfonso J. Zozaya,
Eduard Bertran Albertí
and Jordi Berenguer-Sau
Dept. of Signal Theory and Communications
Polytechnic University of Catalonia
Barcelona, Spain
Nowadays, feedforward is the most effective and broadly used linearization technique employed in modern multi-carrier communications systems. Different versions, in which the key operating parameters are adjusted by means of some mechanisms of automatic adaptation, have been developed and patented.15 The key aspects of the feedforward linearization technique are the amplitude and phase imbalances as well as the inequality of the signal delays among the different branches which are compared. In this article a brief description of a typical feedforward architecture is made and the simulation results of a compensation technique for these imbalances using the least mean square (LMS) algorithm, implemented entirely in the analog domain, are presented.
FEEDFORWARD TECHNIQUE
The architecture of the well-known feedforward linearizer has the form illustrated in Figure 1. Since the power amplifier (PA) presents amplitude and phase distortion, it will be assumed that its out-put is made up of an amplified version of the input signal plus certain intermodulation (IMD) products. These IMD products occupy the same frequency band as the input, the in-band distortion and a spectrum of frequencies outside of the band of interest, the out-of-band distortion. Ideally, the linearization technique of the amplifier aims to eliminate completely the distortions present in the PA output signal. Following this argument the principle of operation of the feedforward linearizer will be described.
|
|
The feedforward linearizer consists of two fundamental circuits -- the signal cancellation circuit and the error cancellation circuit. In the former, an error signal that contains the IMD products generated in the PA is obtained. This error signal is the result of the comparison of a sample of the PA output signal, appropriately attenuated, with a properly retarded sample of the input signal. This combination is usually carried out in a 180° combiner.1 In the latter, the error cancellation circuit, the error signal obtained in the previous circuit is appropriately amplified and injected in opposite-phase to the output to cancel the IMD introduced by the PA. Before the combination, the PA output is suitably delayed. The combination of the error signal with the PA output signal usually takes place in a power directional coupler.1 For simulation purposes the equivalent complex baseband model is shown in Figure 2. The delays among the branches are theoretically compensated. The PA and the error amplifier are represented by the complex gains G and g, respectively. While G is a function of the input signal amplitude, g is assumed to be a constant, which implies a linear operation of the error amplifier. The terms 1/k1 and 1/k2 represent the coupling factors of the directional couplers used in the signal cancellation circuit and the error cancellation circuit, respectively. The complex quantities a and b constitute adjustable parameters for the compensation of the gain and phase imbalances among the branches that are compared.
|
|
The PA input, in a generic case, can contain several independent digital signals, and each one can carry information as much from the phase as in the amplitude. In the first approach, a single input signal is assumed that only carries information with regard to phase, with a complex envelope of the form
vin = cej (t) (1)
(t) (1)
As previously mentioned, the nonlinear PA introduces amplitude and phase distortion. Taking as reference the signal from Equation 1, the PA output is
Va = Gl vin + vIMD (2)
where
Gl = |Gl |ej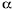 = the linear gain of the PA
= the linear gain of the PA
Gl vin = amplified version of the input signal plus a certain phase shift 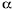
vIMD = intermodulation products
In the signal cancellation circuit a fraction of the PA output signal va /kl , with kl real, is compared with a sample of the input signal avin , with a complex, resulting in an error signal v*i given by
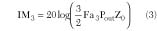
If a is adjusted in such a way that

the error signal **i will contain only the intermodulation products.
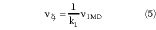
In order to adjust these gain and phase imbalances accurately, the complex parameter a will be altered by means of an adaptive procedure. In a similar way, in the error canceling circuit, the error signal is amplified in a second amplifier, the error amplifier, to obtain
v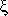 0 = gv
0 = gv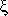 i (6)
i (6)
g = |g| ejß is the gain of the second amplifier. In a way similar to the previous case, the gain and phase of the signal va will be adjusted by means of the complex parameter b, before comparing it to the signal v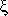 0 to obtain an output signal v0 free of distortions
0 to obtain an output signal v0 free of distortions
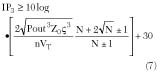
where k2 is real.
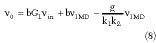
If b is adjusted such that
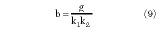
the equation for *0 becomes
v0 = bGvin (10)
The complex parameter b will be adjusted by means of an adaptive algorithm similar to the one used with the parameter a.
Currently, an exact evaluation of the parameters a and b in order to achieve an exact error signal as in Equation 5 and an output signal free of intermodulation products as in Equation 10, respectively, presents insurmountable theoretical and practical difficulties. From a theoretical point of view, if the time delays among the different branches are assumed to be equal, a cancellation of the intermodulation products is possible for the simple case presented previously. The situation becomes more complicated if the input signal presents a time-varying amplitude. In this case the PA complex gain will also vary with time as a function of the amplitude of the input signal. Consequently, it will be impossible to cancel the input signal completely in the signal canceling circuit, unless the parameter a could be adjusted with a higher speed than the speed of change of G. If, on the other hand, the case of an input signal made up of several digital signals such as the one described in Equation 1, with each having a different carrier, is considered, it will be impossible to obtain their total cancellation in the signal canceling circuit by using only one correction loop. In principle, to obtain the intermodulation products, it will be necessary to include as many correction loops as there are different carriers.
Practically, the accuracy in the estimate of the parameters a and b is limited by the amount of processing that is used and by the inherent limitations of the adaptive methods employed. A detailed analysis of the different methods used for the estimate of the parameters a and b is outside the purpose of this article and is a topic open to new possibilities.
The equality shown in Equation 9 can be achieved only for values of g/k1 k2 ≈ 1 and therefore the error amplifier gain must be comparable to the coupler losses 1/k1 k2 . In these circumstances, the linearity premise of the error amplifier supposes an operating point much below saturation. If its 1 dB compression point is comparable with that of the main amplifier, such an operation is allowed because the input signal of the error amplifier is composed only of the IMD terms. Some practical considerations on this problem are presented by Cripps.1 There is a compromise between the amount of IMD reduction and the error amplifier compression characteristics.
ADAPTIVE SOLUTION
An effective and recent solution for an adaptive estimate of the complex parameters a and b includes the use of digital signal processing (DSP) in both cancellation circuits. In this approach, the convergence of the signal canceling circuit must be achieved first in order to avoid stability problems.2
A similar adaptive structure in which the processing is carried out entirely in the analog domain is proposed instead of using a digital architecture based on DSP. This solution supposes great robustness and circuit simplicity, but in its basic version does not allow a precise estimate of the parameters a and b. The analyses will start first with a basic architecture and then the hardware will be expanded to increase the precision of the estimate of the parameters a and b gradually, until an acceptable level is achieved.
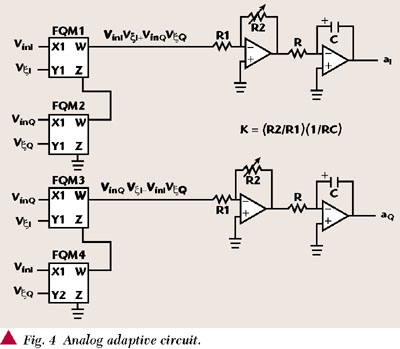
The complex parameters a and b will be adjusted according to the LMS algorithm implemented in the analog domain. Only the equations corresponding to the adaptation of parameter a are developed with the assumption that the same ones are completely applicable to the parameter b.
According to the LMS algorithm, the equations for a are given by
a(n) = a(n 1) + Δ  vin (n)
vin (n) 
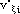 (n) (11)
(n) (11)
a(n) a(n 1) =
K  Δ
Δ 
 vin (n)
vin (n) 
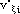 (n) (12)
(n) (12)
where
K = constant of adaptation that fixes the algorithm adaptation speed
vin ( ) = PA input signal
) = PA input signal
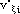 (
( ) = complex conjugate of the error signal described by Equation 3
) = complex conjugate of the error signal described by Equation 3
Equation 12 can take the equivalent form
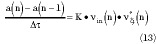
Taking the limit for * approaching zero and assuming a(*) to be analytic,
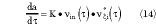
and the actual expression for a is obtained as
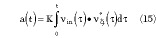
Equation 15 can be implemented in baseband, or in a relatively low intermediate frequency (in an analog way) using operational amplifiers and analog four-quadrant multipliers.
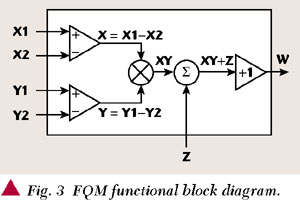
The functional block illustrated in Figure 3 represents a four-quadrant multiplier (FQM).
|
|
Taking into account that
vin (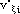 ) = vinI + jvinQ (
) = vinI + jvinQ (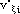 I + jv
I + jv  iQ ) (16)
iQ ) (16)
where the sub-indexes I and Q refer, respectively, to the in-phase and quadrature components of the corresponding signal. It follows that
vin  v*
v*  i = (vinI
i = (vinI  v
v iI
iI
+ vinQ  v*
v* iQ )
iQ )
+ j(vinQ  v*
v* I vinI
I vinI
 v
v iQ ) (17)
iQ ) (17)
Considering the previous result, eight four-quadrant multipliers will be required -- four for the multiplication
vin ( )
)  v*
v*  i (
i ( ) for the estimate of parameter a, and four for obtaining the product v
) for the estimate of parameter a, and four for obtaining the product v i (
i ( ) * v* o (
) * v* o ( ) to estimate parameter b. The sums required in each complex multiplication as well as the conjugation of the factors could be implemented using the same FQM. The resulting analog adaptive circuit is shown in Figure 4.
) to estimate parameter b. The sums required in each complex multiplication as well as the conjugation of the factors could be implemented using the same FQM. The resulting analog adaptive circuit is shown in Figure 4.
|
|
SIMULATION RESULTS
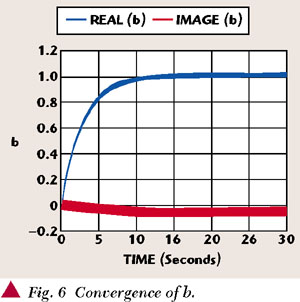
The architecture shown in the complex baseband equivalent circuit has been simulated for an input signal made up of two tones at 0.1 and 0.15 Hz per sample, respectively. Figure 5 shows the convergence curves for parameter a, while Figure 6 shows the convergence curves for parameter b. In Figures 7, 8 and 9 the spectra of the signals of interest are illustrated starting from which the proposed solution can be arrived at.
|
|

|
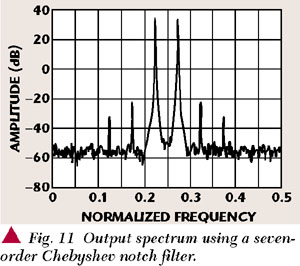
It can be seen from the convergence of b that it exhibits a high misadjustment. The superimposed noise on parameter b has the same form as the input signal vin ( ) and is due to the higher power of this signal compared with the IMD products that it is expected to suppress. This situation does not allow a reduction of all the IMD harmonics and, on the contrary, the smaller power IMD components are magnified. The described situation can be appreciated when comparing the output spectrum with the main power amplifier output. This unwanted effect can be eliminated by using a notch filter that suppresses the signal in the LMS adapter that estimates a, as proposed by S.J. Grant.2 Using a Chebyshev seven-order notch filter with a stop-band that coincides with the vin bandwidth, an acceptable result is achieved. The curve of convergence of the parameter b is notably improved (Figure 10) and the harmonic of smaller power are discriminated and suppressed at the output (Figure 11).
) and is due to the higher power of this signal compared with the IMD products that it is expected to suppress. This situation does not allow a reduction of all the IMD harmonics and, on the contrary, the smaller power IMD components are magnified. The described situation can be appreciated when comparing the output spectrum with the main power amplifier output. This unwanted effect can be eliminated by using a notch filter that suppresses the signal in the LMS adapter that estimates a, as proposed by S.J. Grant.2 Using a Chebyshev seven-order notch filter with a stop-band that coincides with the vin bandwidth, an acceptable result is achieved. The curve of convergence of the parameter b is notably improved (Figure 10) and the harmonic of smaller power are discriminated and suppressed at the output (Figure 11).
|
|
The IMD reduction achieved is appreciably better but it is not of the typical order of magnitude reported in the references1,2,4,5 for the same linearization technique. The apparently hidden reason resides on the way the parameter a is obtained. Indeed, in the error signal spectrum shown, the wanted signal is considerably reduced, but at the price of introducing additional intermodulation components in quadrature with the intermodulation components that are expected to be eliminated. The problem is solved again by limiting in frequency the correlation of the signals vin and v i to the band of the signal vin with a seven-order bandpass Butterworth filter. The spectrum of the output signal is illustrated in Figure 12 for this case.
i to the band of the signal vin with a seven-order bandpass Butterworth filter. The spectrum of the output signal is illustrated in Figure 12 for this case.
CONCLUSION
An acceptable estimate of the complex parameters a and b for the amplitude and phase imbalances compensation in the signal cancellation circuit and the error cancellation circuit, respectively, of a feedforward linearizer was possible, using analog processing of the corresponding signals. A basic adaptive structure based on the analog LMS algorithm was analyzed and simulated. With the basic architecture, a 30 dB reduction of the larger harmonics was attained, but those of smaller power were lightly magnified. By including two seven-order Chebyshev notch filters in the estimate of b this unwanted effect was eliminated. By including two seven-order Butterworth bandpass filters in the estimate of a, an IMD reduction of 50 dB was achieved. Although the latter result is similar to those accomplished by means of other implementations of the feedforward linearization technique, the current realization exhibits the added advantage that the circuitry is totally analog, and can be implemented with simple hardware. *
References
1. S.C. Cripps, "RF Power Amplifiers for Wireless Communication," Artech House, 1999, pp. 267279.
2. S.J. Grant, J.K. Cavers and P.A. Goud, "A DSP Controlled Adaptive Feedforward Amplifier Linearizer," Proc. IEEE Intl. Conf. Universal Personal Commun, Cambridge, MA, Sept. 29Oct. 2, 1996,
pp. 788792.
3. J.K. Cavers, "Adaptive Feedforward Linearizer for RF Power Amplifiers," US Patent Serial No. 5,489,875, February 6, 1996.
4. Q. Cheng, C. Yiyuan and Z. Xiaowei. "A 1.9 GHz Adaptive Feedforward Power Amplifier," Microwave Journal, Vol. 41, No. 11, November 1998, pp. 8696.
5. W.T. Thornton and L.E. Larson. "An Improved 5.7 GHz ISM-band Feedforward Amplifier Utilizing Vector Modulator for Phase and Attenuation Control," Microwave Journal, Vol. 42, No. 12, December 1999, pp. 97106.








 Meng-Chung Tsai was born in Kaohsiung, Taiwan, the Republic of China, in 1974. He received his MSEE degree from National Cheng Kung University, Tainan, Taiwan, in 2000. He worked on Ka-band printed antennas for his master study. Currently he is with the Acer NeWeb Corp. (ANC) as a R&D engineer. His research interests include antenna and RF design for wireless communication systems.
Meng-Chung Tsai was born in Kaohsiung, Taiwan, the Republic of China, in 1974. He received his MSEE degree from National Cheng Kung University, Tainan, Taiwan, in 2000. He worked on Ka-band printed antennas for his master study. Currently he is with the Acer NeWeb Corp. (ANC) as a R&D engineer. His research interests include antenna and RF design for wireless communication systems.  Huey-Ru Chuang was born in Tainan, Taiwan, the Republic of China, in 1955. He received his BSEE and MSEE degrees from the National Taiwan University, Taipei, Taiwan, in 1977 and 1980, respectively, and his PhD degree in electrical engineering from Michigan State University, East Lansing, MI, in 1987. From 1987 to 1988, he was a postdoctoral research associate at the Engineering Research Center, Michigan State University. From 1988 to 1990, he was with the Portable Communication Division, Motorola Inc., Ft. Lauderdale, FL. He joined the department of electrical engineering, National Cheng Kung University, Tainan, Taiwan in 1991, where he is a professor. His research interests include antenna and RF/microwave circuits design for wireless communications, electromagnetic computation of the human interaction with portable antennas and EM fields, satellite reflector antennas, EMI/EMC, and microwave communication and detection systems. Professor Chuang can be reached at
Huey-Ru Chuang was born in Tainan, Taiwan, the Republic of China, in 1955. He received his BSEE and MSEE degrees from the National Taiwan University, Taipei, Taiwan, in 1977 and 1980, respectively, and his PhD degree in electrical engineering from Michigan State University, East Lansing, MI, in 1987. From 1987 to 1988, he was a postdoctoral research associate at the Engineering Research Center, Michigan State University. From 1988 to 1990, he was with the Portable Communication Division, Motorola Inc., Ft. Lauderdale, FL. He joined the department of electrical engineering, National Cheng Kung University, Tainan, Taiwan in 1991, where he is a professor. His research interests include antenna and RF/microwave circuits design for wireless communications, electromagnetic computation of the human interaction with portable antennas and EM fields, satellite reflector antennas, EMI/EMC, and microwave communication and detection systems. Professor Chuang can be reached at