A confluence of advances in low cost digitally controllable RF metamaterial-based apertures and real-time embedded cognitive signal processing has afforded a new opportunity to realize a distinctly new and affordable low SWAP smart antenna capability for a multitude of demanding applications from communications to radar. This article provides an overview of these enabling advances, their synergistic combination, and the new markets that are emerging as a result.
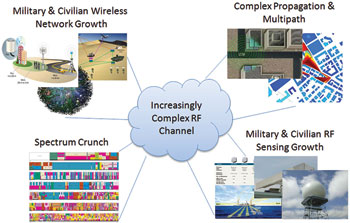
Figure 1 A confluence of stressing factors is conspiring to create significant challenges to next generation RF systems.
![]() Watch Video
Watch Video
IMS 2011 Closing Session Featuring Dr. Guerci
Motivation for Next-Gen Smart Antennas
From wireless communications to RF sensing (radar, SIGINT), operating environments are becoming ever more challenging due to a multitude of factors from the “spectrum crunch” resulting from a global proliferation of wireless and RF sensing systems, to complex clutter and multipath/propagation backgrounds2,3 (see Figure 1). This emerging challenge is concurrent with continual demands for greater performance from end users. Consequently, there is a perennial need for systems that can adapt continuously to an ever changing transmission channel in an “intelligent” and sophisticated way.
Theoretically, one path forward is through real-time spatio-temporal adaptivity powered by flexible RF hardware and back-end cognitive signal processing.4 While there has been steady and measureable progress in real-time software that powers cognitive software defined radios (SDR) and radar,5,6 the analog hardware “in front of the analog-to-digital-converter (ADC)” has remained a stubborn challenge due to inherent physical and cost challenges.7
However, recent breakthroughs in affordable software defined apertures (SDA) enabled via new RF metamaterial designs are opening up both new levels of adaptive antenna affordability as well as performance and control. Though the functionality of the SDAs is similar to electronically scanned antennas (ESA), the former term can be used to reflect the significantly distinct architecture. In particular, the metamaterial SDA can be considered a dynamically tuned but passive antenna, due to the absence of power amplifiers and distinct radio modules distributed throughout the aperture.
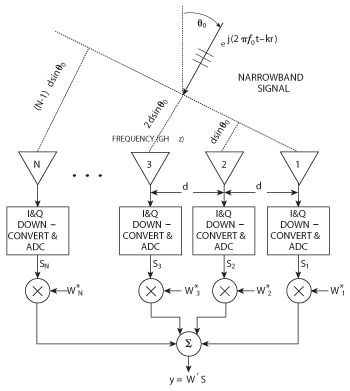
Figure 2 Example of a modern digital phased array antenna (receive) illustrating the need for independent RF and digital channels (Courtesy of reference 1).
In this article, we provide an overview of the latest advances in new affordable ESA technologies, and the real-time cognitive signal processing that can take maximal advantage of the available adaptive degrees-of-freedom (DoF). Also discussed are the latest breakthroughs in RF metamaterials that are enabling an entirely new generation of affordable low size, weight, power and cost (SWaP-C) SDAs for a variety of applications. Then the state-of-the-art in cognitive signal processing and real-time embedded computing—the “smarts” behind smart antennas—is reviewed. Finally, it is all put together exploring the many problems to which next generation affordable smart antennas can be applied.
Next Generation Low SWaP-C ESAs
Electronically scanned antennas have enabled countless RF applications where fixed beam and/or mechanically gimbaled apertures are not viable solutions. Interestingly, achieving electronic scan capability from the very beginning utilized phased array concepts,8 which of course is just one way to achieve electronically controlled scanning. In a phased array (see Figure 2), the constructive/destructive property of electromagnetic (EM) waves emanating from different subapertures is exploited to shape the composite antenna pattern. For a passive ESA, this is achieved by transmitting an identical waveform (possibly amplitude tapered for sidelobe control), emanating from a single high power source, from different subapertures with an appropriate phase shift (narrowband) or time delay (wideband) to achieve a desired beam shape.
In an active ESA (AESA), each subaperture is capable of transmitting as well as receiving. Note that the physics of this approach, as well as numerous practical considerations and constraints, often results in a relatively large SWaP-C footprint. For example, if one desires a high gain mainbeam with low sidelobes, as well as adaptive beamforming to spatially filter interference, a generally complex ESA is required with a relatively large number of independent subapertures and channels.1Moreover, the full power of an ESA is only realized if it can be digitally controlled which, unfortunately, leads to the requirement for separate ADCs in each receive channel. Realizing that the number of channels tends to grow in proportion to the area of the antenna leads inexorably to an approach whose SWaP-C does not scale well as requirements grow.
Guerci has firsthand experience with the difficulties of achieving a low SWaP-C ESA. During his seven years with the Defense Advanced Research Projects Agency (DARPA), numerous advanced projects were executed precisely to achieve low SWaP-C antennas for everything from low cost cruise missile defense (LCCMD) to multi-function RF and MEMS based phase shifters (see Figure 3 and reference 9). While these projects achieved modest success, in the end, it was mostly due to leveraging the major advances taking place in the commercial wireless RF sector.9 The “DARPA-esque Holy Grail” of achieving an order of magnitude reduction in SWaP-C remained elusive.
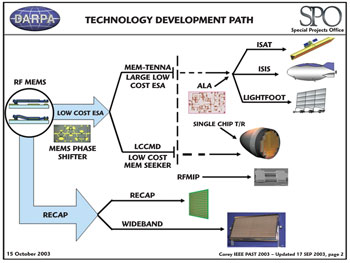
Figure 3 An excerpt from a presentation by Dr. Larry Corey (DARPA/SPO) overviewing the multipronged approach to achieve lower cost yet high performance ESAs (reference 9).
In hindsight, the reasons are obvious: An ESA approach that is based on multiple independent RF channels can only be made so cheap and compact. Ironically, if one consults an elementary text on EM theory to determine how to achieve a desired antenna pattern from first principles, one finds a much more general solution than a phased array. Specifically, and without going into too much detail, the far field antenna pattern is the Fourier transform of the RF aperture distribution (see Figure 4).10 This naturally begs the question: “How can one digitally control the aperture distribution without the use of phased array approaches?” One answer, the use of RF metamaterials, has proven to be remarkably successful.
![]() Watch Video
Watch Video
Kymeta Metamaterials Technology
Beginning in the 1990s, researchers began to explore RF metamaterials that could exhibit properties not found in naturally occurring substances—such as so-called “negative refractive index” materials.11Of course, the usual “Hype Curve”12 kicked in with exaggerated hopes and expectations. Within the past few years however, solid applications exploiting RF metamaterials have emerged and have even led to commercial product lines.

Figure 4 Under fairly general conditions, the far field antenna pattern is proportional to the Fourier transform of the CF (•) aperture function A(x, y) (Fraunhofer approximation10).

Figure 5 Sample MSA-T ESA for satellite communication applications (see www.kymetacorp.com).
One particular application of metamaterials for SDAs that function as low SWaP-C ESAs is being developed by engineers and scientists at the Metamaterials Commercialization Center (MCC) that is a part of Intellectual Ventures (IV), working in cooperation with Duke University.11Figure 5 shows an example of IV’s metamaterials surface antenna technology (MSA-T) as applied to a commercial satellite communications application. Electronic scan capability (transmit or receive) is achieved by launching a wave across a surface with embedded RF resonant elements as shown in Figure 5. By a judicious selection of digitally controlled resonant elements, and spacings, any desired antenna pattern can be formed with the available DoF as shown in Figure 6. It should be noted that this approach can be more efficient than so-called “leaky” waveguide approaches.13
![]() Watch Video
Watch Video
Intellectual Ventures' Metamaterial Surface Antenna Technology
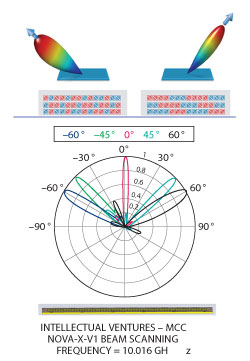
Figure 6 Illustration of the RF metamaterial SDA. By judicious digitally controlled tuning of the resonant elements, an arbitrary steerable antenna beam (or beams) can be formed.
Some of the key advantages of the MSA-T SDA approach include:
- Eliminates the need for multiple independent RF channels and associated phase shifters or time delay units (TDU) (i.e., it is not a phased array approach).
- Large electronic scan angles (±60°) are possible (see Figure 6), unlike traditional leaky wave antennas.
- Can be synthesized using conventional printed circuit board (PCB) manufacturing methods (see Figure 5).
- Additional adaptive DoFs can be introduced without introducing more RF channels (just more low power digital control lines and resonant elements).
- Inherently low physical volume and, especially, low profile (e.g., a few mm thick).
- Inherently low cost due to aforementioned architecture and PCB compatibility.
- Can realize radiation efficiencies comparable to parabolic dish and other conventional antennas.
- Enables the potential for delivering a true conformal aperture that performs just as effectively as a planar aperture (to within projected aperture constraints).
A “digitally” controllable, adaptive and flexible aperture is certainly a necessary prerequisite for a smart antenna—but not sufficient. Next we survey the latest advances in the back-end signal processing that is the “brains” of smart antennas.
Next Generation Intelligent Signal Processing
The original term “smart antenna,” as coined by Winters,14 referred to spatial diversity and adaptive beamforming. Of course the “smarts” were achieved via real-time adaptive digital signal processing (DSP). In the past 10 years or so, even more sophisticated real-time adaptive processing has been developed that from an “input-output” perspective exhibits a very high degree of machine intelligence and environmental awareness. It has thus become necessary to develop newer nomenclature such as “cognitive processing” (e.g., cognitive radios,15cognitive radar,5,16etc.) to make clear the significant advancements that have been achieved.
A definition of cognition that has surprising engineering applicability is afforded by the National Institute of Health (NIH):17
Cognition: Conscious mental activity that informs a person about his or her environment. Cognitive actions include perceiving, thinking, reasoning, judging, problem solving and remembering.

If we replace “person” with “system,” and “his or her” with “its,” we can readily map the above attributes into those associated with machine intelligence as in Table 1.5 The goal of any intelligent RF system is to optimize system performance based on ever changing knowledge of the RF channel and user demands. In general, the biggest challenge is real-time channel knowledge due to the extreme nonstationary and complex nature of a realistic RF channel due to highly complex multipath scattering and terrain interaction, as well as highly chaotic electromagnetic interference (EMI).
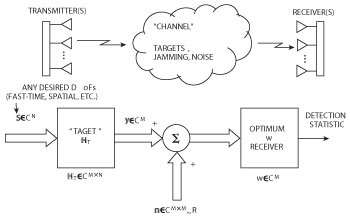
Figure 7 Example of a MIMO forward path problem where it is desired to jointly optimize both the transmit and receive functions to maximize SINR.
The importance of knowing the RF channel is easily illustrated with a relatively simple signal-to-interference-plus-noise ratio (SINR) optimization problem. Figure 7 shows that a simple forward RF channel model consists of an N-dimensional complex valued transmit signal S ∈ CN, a signal-to-receiver multi-input, multi-output (MIMO) stochastic transfer function represented by  ∈ CN × N(which in the case of radar includes a target transfer function), and additive interference ñ ∈ CN with associated covariance R ∈ CN × N. The goal of the receiver, represented by w ∈ CN, is to (for example) maximize the output SINR. Details of the solution can be found in reference 5, which are stated here:
∈ CN × N(which in the case of radar includes a target transfer function), and additive interference ñ ∈ CN with associated covariance R ∈ CN × N. The goal of the receiver, represented by w ∈ CN, is to (for example) maximize the output SINR. Details of the solution can be found in reference 5, which are stated here:

where H+= HwH, and Hw is the “whitening filter” (Hw= R-½).18 The key take away from these two fundamental equations is the need for knowledge of the channel propagation and interference. How does one get this knowledge in a rapidly varying environment and act on it in real time? This is indeed the raison d’être for cognitive RF systems.
Intelligent Channel Estimation
In both wireless communications and radar, there are two fundamental contributors to the time-varying channel parameters: (1) Propagation; and (2) Co-Channel Interference. Traditionally, relatively simple adaptive signal processing techniques, coupled with basic statistical models, were employed to estimate both (1) and (2). Suffice to say these approaches have run their course—hence the emergence of so-called cognitive radio/radar. There is now a variety of new “intelligent” signal processing methods emerging for both propagation and interference channel estimation. We will highlight some of the more advanced techniques.
What if a radio knew ahead of time that it was about to hit a significant fade? Or conversely be blasted by a co-channel interferer? Or if it knew that steering its antenna pattern 20° to the left would result in a 10 dB improvement in SINR? In many applications, events like this can be the result of complex terrain/multipath interactions. In principle, if a radio knew its precise location and had accurate 3D knowledge of its surroundings and possibly relevant meteorological data, it could “calculate” the propagation channel and thus predict a multitude of important effects. To do this in practice, however, the radio would need to perform complex electromagnetic ray tracing and wave propagation calculations, and have access to digital terrain databases, etc. Additionally, if propagation measurements were routinely performed and stored, then over time a historical database could be created and likewise utilized to predict performance. Why not combine both these approaches?
In the early 2000s, DARPA started a major project to do just that for radar. Dubbed the KASSPER project (Knowledge-Aided Sensor Signal Processing and Expert Reasoning),19 the goal was to achieve an order-of-magnitude or better detection performance improvement in a challenging ground moving target indicator (GMTI) application (a good example of a major GMTI radar is the U.S. Air Force’s JSTARS20). Though there are many intricate details, the crux of the KASSPER concept can be illustrated with a relatively simple mathematical example.
One of the specific key goals of KASSPER was to achieve significantly better clutter cancellation performance. In particular, improvement was sought in the space-time adaptive processing (STAP) filter.1 Without belaboring the details, a STAP filter is essentially an adaptive multichannel finite impulse response (FIR) filter whose optimum weights (“taps”) w ∈ CN obey the well-known Wiener-Hopf equation:1
w= R-1s (3)
where R ∈ CN × Nis the interfering clutter plus noise covariance matrix, and S ∈ CN is the desired target (“steering vector”) of interest (i.e., direction, Doppler, etc.). In STAP applications, the dimensionality of R can be relatively large, and thus require a lot of training data to estimate. For example, a bedrock of STAP is the so-called maximum likelihood estimate (MLE) which substitutes an estimate of R in the filter equation, denoted as Rˆ MLE, given by
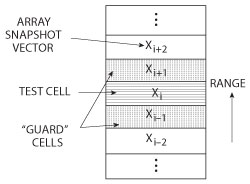
Figure 8 Illustration of a popular training strategy for computing the requisite statistics in STAP applications (Courtesy of reference 1).
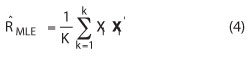
where the K samples {Xi ∈ CN} correspond, for example, to the space-time signals received by the radar over K range bins1. An illustration of this training approach is shown in Figure 8. If one is fortunate enough to be operating over homogenous clutter terrain, than the “stationarity” assumption implicit in this sample matrix approach works very well, and near optimal clutter cancellation performance is achievable. Of course in the real world, radars can be operating in extremely complex clutter terrains, such as urban settings resulting in very suboptimal performance that has been well documented in the literature.1,21 How did the KASSPER project remedy this with cognitive signal processing?
The approach that resulted in the best overall performance averaged over a number of different scenarios had a structure in the form of:

where  MLE is as before but with far fewer training samples that are much closer to the range bin of interest—and thus very representative of the actual clutter, and
MLE is as before but with far fewer training samples that are much closer to the range bin of interest—and thus very representative of the actual clutter, and  KA is the knowledge-aided (KA) estimate of the clutter covariance obtained from a variety of model-based and cognitive signal processing techniques. In some variants, it has a very similar mathematical form as the MLE estimator, but instead of using measured range samples, synthetic samples were generated using either ray tracing or synthetic aperture radar (SAR) images of the region of interest. The former is an example of the model-based ray tracing approach while the latter is an example of the database approach where the SAR image acts as the “database.”5Thus the best overall intelligent signal processing approach was a blend of “live” data, model based predictions and historical databases—hard to argue with. Indeed without getting too philosophical, it’s a lot like the way we interact with the world—prior experience, problem solving and learning, hence the term cognitive.
KA is the knowledge-aided (KA) estimate of the clutter covariance obtained from a variety of model-based and cognitive signal processing techniques. In some variants, it has a very similar mathematical form as the MLE estimator, but instead of using measured range samples, synthetic samples were generated using either ray tracing or synthetic aperture radar (SAR) images of the region of interest. The former is an example of the model-based ray tracing approach while the latter is an example of the database approach where the SAR image acts as the “database.”5Thus the best overall intelligent signal processing approach was a blend of “live” data, model based predictions and historical databases—hard to argue with. Indeed without getting too philosophical, it’s a lot like the way we interact with the world—prior experience, problem solving and learning, hence the term cognitive.
This is all well and good but the astute reader is by now no doubt wondering about the potentially daunting computational burden associated with this approach for real-time applications. Indeed, when the KASSPER project was started over 10 years ago, it was the challenge of trying to implement these ideas in a high performance embedded computer (HPEC) that was the true crux of the project. This was before the advances in FPGAs, ASICs and multi-core GPUs for embedded applications over the past decade, that have greatly expanded the range of cognitive techniques that can be implemented in real-time.5 Nonetheless, the non-device specific techniques developed under KASSPER for achieving real-time performance are still very applicable and often still necessary. We will briefly discuss two of the methods developed under KASSPER.
The first method for reducing real-time KA processing is simply prioritization based on relatively simple knowledge and ownship kinematic knowledge. For example, if a radar knows where it will be located, say, a few seconds into the future (if it doesn’t, it has far bigger problems), it can perform a “look-ahead” function in parallel with the real-time processing and search the terrain database for “troubled” spots. In the case of GMTI radar, these might be regions of complex terrain, land-sea interfaces, or very large reflectors (known as “discretes”). Not all “inhomogeneities” have the same deleterious impact on performance. Thus a natural rank ordering of the trouble spots emerges. This can then be subjected to a resource allocation function that decides how to best use onboard computational resources. Keep in mind that this is all happening “in the future,” i.e., in a predictive mode. The radar has not yet encountered the next scene—but it can easily anticipate it a few seconds into the future, often even longer. This look-ahead approach is also essential when interacting with onboard databases that reside in memory. There is simply no way for a highly vectorized real-time processor to interact with slower memory and keep up. An analogous prioritization scheme is easily developed for a variety of non-radar applications such as wireless mobile communications where, for example, prior knowledge of impending channel changes can be used to again optimize resources and performance.
The second method developed under KASSPER for achieving real-time KA processing was to perform the necessary calculations BEFORE the radar returns arrive. This was again achieved using the aforementioned look-ahead approach, but it also utilized the radar resource scheduler to obtain critical and necessary information such as what operating frequency, waveform/bandwidth, polarization, scan angle and patterns will be used in the future. With this information, the aforementioned synthetic KA covariances could be calculated and literally “appended” to the actual real-time data stream.1,5 Thus in short, the seemingly insurmountable obstacles associated with performing KA and cognitive functions were overcome with prior knowledge, physics calculations and ownship resource scheduler knowledge.5
A third method for achieving real-time KA/cognitive capabilities had nothing to do with KASSPER. It is simply the result of the advances achieved in the past decade with embedded ASICs, FPGAs, multi-core CPUs and especially general purpose GPUs. Indeed it is rather ironic that the “real-time” graphical rendering and ray tracing requirements of video games has ushered in entirely new ways to perform real-time sensor and communication signal processing exploiting the very same types of calculations. Thus from an algorithmic/software and real-time hardware stance, the technical excuse is “off the table.” It is now absolutely possible to implement truly “intelligent” real-time sensor/comms signal processing that knows where it is in relation to its environment, has access to a plurality of knowledge and modeling sources, and can act on the knowledge in a way that for all intents and purposes mimics cognitive abilities.

Figure 9 UAVs represent one of the most demanding and growing applications for a multitude of low SWaP-C electronically scanned antennas.
Putting it All Together: The Path Ahead
While cognitive RF systems have been successfully demonstrated with high-end adaptive antenna systems (e.g., the DARPA KASSPER project), it is now possible to leverage these techniques and advances in low SWaP-C HPEC and SDAs and apply them to a whole range of heretofore cost and SWaP prohibitive applications. For example, UAVs are inherently SWaP-C limited due to both their relatively small size and need to maximize their operational flight envelope (speed, altitude, range). Nonetheless, there are countless missions and demands that UAVs are poised to fulfill if only they could maximize their payload effectiveness in a cost effective way. For example, there is great interest in outfitting UAVs with GMTI radars. While large UAVs such as the Predator and Global Hawk can support reasonably powerful systems with conventional AESAs, the vast majority of smaller UAVs must settle for far less powerful and capable radars. Indeed due to the relatively high SWaP-C nature of AESAs, static or mechanically steered antennas are often utilized which lack the necessary DoFs to fully exploit cognitive signal processing. Fortunately, with maturation of the aforementioned metamaterial SDAs, it now appears that technical obstacle has been removed. Moreover, even larger UAVs may want to take a second look at replacing their AESAs with metamaterial ESAs—SWaP-C is still very much a major concern no matter what the class of UAV (see Figure 9).
As mentioned at the beginning of this article, the term “smart antenna” originally referred to ESAs (or multi-antenna) wireless communication systems. However, over the years, only a modest rollout of AESAs for communications has been achieved again due to their inherently high SWaP-C nature. Here again is another opportunity to re-visit a multitude of wireless applications armed with next gen low SWaP-C powered by state-of-the-art embedded cognitive processing.
Lastly, but by no means least, RF spacecraft payloads represent a major class of severely SWaP-C constrained applications. Every pound of payload costs $10,000 to boost into low Earth orbit (LEO), and every cubic foot takes up precious space in the rocket faring.21 Extremely low SWaP-C ESAs powered by onboard intelligent embedded processing open up entirely new application possibilities from remote sensing, surveillance and satellite communications.
In summary, a confluence of advances in low SWaP-C digitally controllable SDAs and real-time embedded cognitive signal processing has afforded a new opportunity to realize a distinctly new affordable smart antenna capability for a multitude of demanding RF applications from communications to radar. The sky’s the limit—or perhaps even beyond!
References
- J.R. Guerci, “Space-time Adaptive Processing for Radar,” Norwood, MA, Artech House, 2003.
- J.R. Guerci, “R&D Panel Overview,” International Symposium on Advanced Radio Technologies (ISART), 2011.
- J. Chapin, “Shared Spectrum Access for Radar and Communications (SSPARC),” DARPA BAA-13-24, www.darpa.mil, 2012.
- J.R. Guerci, “Cognitive Radar: The Next Radar Wave?” Microwave Journal,January 2011, pp. 22-36.
- J.R. Guerci, Cognitive Radar: “The Knowledge-Aided Fully Adaptive Approach,” Norwood, MA, Artech House, 2010.
- J. Mitola, “Cognitive Radio for Flexible Mobile Multimedia Communications,” IEEE International Workshop on Mobile Multimedia Communications,1999 pp. 3-10.
- W. Chappell, www.darpa.mil/NewsEvents/Releases/2013/02/26.aspx.
- K.F. Braun, “Electrical Oscillations and Wireless Telegraphy,” presented at the Nobel Lecture, 1909.
- L. Corey et al, “Phased-array Development at DARPA,” presented at the IEEE International Symposium on Phased Array Systems and Technology, 2003.
- H.E. White and F.A. Jenkins, Fundamentals of Optics, 3rd ed., McGraw-Hill, 1957.
- D. Smith et al, “Metamaterials and Negative Refractive Index,” Science, Vol. 305, pp. 788-792, 2004.
- http://en.wikipedia.org/wiki/Hype_cycle.
- A.W. Snyder, “Leaky-ray Theory of Optical Waveguides of Circular Cross Section,” Applied Physics, Vol. 4, pp. 273-298, 1974.
- J.H. Winters, “Smart Antennas for Wireless Systems,” Personal Communications, IEEE, Vol. 5, pp. 23-27, 1998.
- J. Mitola III and G.Q. Maguire Jr., “Cognitive Radio: Making Software Radios More Personal,” Personal Communications, IEEE, Vol. 6, pp. 13-18, 1999.
- S. Haykin, “Cognitive Radar: a Way of the Future,” IEEE Signal Processing Magazine, Vol. 23, pp. 30-40, 2006.
- Definition of Cognition, National Institutes of Health, National Institute of Mental Health, http://science-education.nih.gov/supplements/nih5/Mental/other/glossary.htm.
- H.L.V. Trees, Detection, Estimation and Modulation Theory, Part I, New York, Wiley, 1968.
- J.R. Guerci and E.J. Baranoski, “Knowledge-aided Adaptive Radar at DARPA: an Overview,” Signal Processing Magazine, IEEE, Vol. 23, pp. 41-50, 2006.
- JSTARS, www.northropgrumman.com/Capabilities/E8CJointSTARS/Pages/default.aspx.
- W.L. Melvin, “Space-time Adaptive Radar Performance in Heterogeneous Clutter,” Aerospace and Electronic Systems, IEEE Transactions, Vol. 36, pp. 621-633, 2000.
- Cost of Launching a Payload into Space, www.nasa.gov/centers/marshall/news/background/facts/astp.html_prt.htm.
