The Application of Low Noise, X-band Synthesizers to QAM Digital Radios

The Application of Low Noise, X-band Synthesizers to QAM Digital Radios

Mark R. Simpson and John M. Dixon

VertiCom Inc.
Santa Rosa, CA

For high data rate, 16-to-64-quadrature amplitude modulation (QAM) designs, the vast majority of wireless point-to-point and point-to-multipoint radio manufacturers currently are using fixed-frequency, mechanically adjustable dielectric resonator oscillators (DRO). The major problem with DRO technology is that the oscillators are fixed frequency. Because of the bandwidth limitation of the DROs, radio manufacturers must design or procure a large number of the oscillators to cover their customers’ (the service providers) anticipated frequency bands. Once the frequencies are allocated, the radio manufacturers must then select the DROs for those specific bands, assemble and test the systems, and ship them to their customers. The net effect is a significant lag in system delivery time to the service providers.

DROs are simple and relatively inexpensive, and have been the designer’s technology of choice for some time where good phase noise performance is required. Radio manufacturers would prefer a DRO design with greater than the typical 200 MHz of mechanical tuning for their high capacity radios. To accomplish this goal of added bandwidth and improved phase noise performance, a combination of voltage-controlled crystal oscillators, DROs or low noise VCOs is required. The simplicity, cost and performance advantages of the individual components soon begin to wane.

Nearly in unison, most of the giants of the point-to-point and point-to-multipoint industry are beginning to talk of a possible synthesized option for their designs. Some manufacturers are already in the design phase; all hope to achieve wider bandwidths, fewer source counts and, of course, lower cost margins in their new generation of radios. Few of these manufacturers have yet to hone the technical requirements for the radio designs to meet the current and near-future demands of the market. The desired end result is a superior product with lower costs to the service providers. Lower costs likely will result in a broader appeal to the service providers and thus more systems will be sold. The increased sales will spur further reductions in the cost of producing the systems due to the economies of scale. So the theory goes…

What has prevented the conversion from fixed oscillators to synthesized, high capacity radios from happening a long time ago? After all, synthesized sources have been on the market for decades. In fact, for the simpler modulation schemes such as frequency-shift keying (FSK) or phase-shift keying (PSK), VCO-based synthesizers have been used successfully to provide low data rate radios for years. For the higher data rate and more complex modulation designs, the VCO-based technology does not meet the minimum phase noise performance requirements.

The performance requirements for the medium-to-high capacity applications are fairly exact. The combination of frequency requirements in the 6 to 38 GHz range, phase noise of < –85 to –90 dBc/Hz at 10 kHz frequency offset and low cost to meet the service provider’s cost targets nearly eliminated most of the available technology options. As a result, radio manufacturers have been locked in to the DRO’s capabilities. DROs are available for as little as $200 for the lower performance devices and, on the high end, $600 for an X-band device with approximately 200 MHz of mechanically adjustable bandwidth. The DROs are simple and reliable, and their electrical performance meets the required specifications. VCO-based synthesizers worked fine for the systems using the simpler FSK or PSK modulation. However, because the Q of the VCO rolls off with increasing frequency, these synthesizers are not considered for QAM applications.

Increased data rates and more complex modulation have placed increased demands on the available spectrum. The speed of the technology advancement has been heavily dependent upon whether the new performance requirements could be met within the desired cost structures. Unlike the VCO, a yttrium iron garnet (YIG)-based oscillator’s Q performance increases with frequency. As a result, the key capabilities of the YIG-based synthesizers are good noise profiles (the YIG-based oscillator offers a 46 dB improvement beyond the FSK requirements, as shown in Figure 1 ) and tuning bandwidths that are more than twice that of the typical VCO designs. Relative to the typical DRO architecture, the YIG design typically offers better than a 150x improvement in bandwidth capability, and simple and reliable designs that are cost effective to produce for the commercial market. For example, assume a radio manufacturer plans to build a radio to cover the International Telecommunications Union (ITU) band at 23 GHz in its entirety. One YIG-based synthesizer would be required with a tuning range of 6.6 to 7.6 GHz. Assuming a 1.5 GHz IF LO, the RF output would be multiplied by three to achieve 21.3 to 24.3 GHz of frequency coverage. This 3 GHz of tuning capability covers the entire ITU band with 600 MHz of bandwidth to spare. The radio manufacturer could deliver 16-QAM-capable radios that tune across the entire band to the service provider prior to frequency allocation. A VCO-based synthesizer design could provide frequency coverage in this range, but not the spectral purity, and only at FSK or PSK modulation. Moreover, the radio designer would require at least two VCO-based synthesizers to cover the entire ITU band. A DRO design could offer the phase noise performance necessary for 16-QAM modulation, but the DRO’s bandwidth limitations would cause a lag in the system delivery time because of the need to factory select the DRO sources that depend upon the required RF. Thus, the DRO approach is not a good choice for the service provider who wants to be up and running before frequency allocation.

Signal Distortions

Several signal distortions occur commonly within the typical RF system that elucidate the spectral purity of the signal source. Phase noise tops the list of least-desired signal flaws, followed by phase hits (or pops) and phase perturbation. These abnormalities contribute to a degradation in the bit error rate (BER) factor, which is a key measure of RF system noise performance.

Phase noise is a random phase excursion of the carrier signal. Generally, a high level of phase noise is associated with a low resonator Q factor and circuit component instabilities. The modulation schemes of most digital communications rely upon accurate phase relation of the signal. Therefore, as the complexity of the modulated system increases, as in a change from a binary PSK (BPSK) to a quadrature PSK (QPSK) modulated system, the system will tolerate less phase noise. As the phase noise is increased, a point will be reached where decision boundaries will be crossed on a regular basis that will result in a dramatic rise in the BER.

With essentially the same RMS phase noise deviation injected into each of three different modulation schemes (BPSK, QPSK and 16 QAM), simulation results indicate graphically the complications that begin to develop. In the simpler BPSK and QPSK modulation schemes, shown in 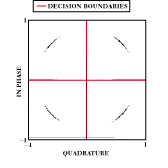Figures 2 and 3 , respectively, there are no violations of the modulation decision boundaries (vertical and horizontal lines on the graphs). Figure 4 shows a significant increase in the modulation complexity to 16 QAM. With 5.53° of injected phase noise, some decision boundaries are being crossed. This phenomenon is known as intersymbol interference. The net result is an increase in the system BER. Of course, the simulations indicate only the effect of phase noise and ignore the likely probability of additional noise factors such as spurious, AM-to-PM conversion and thermal noise.

Phase hits and pops are the results of a number of mechanical and environmental conditions, such as inferior resonator contacts, defects in the resonator’s crystalline structure or poor quality in solder connections. Other possible causes include electromagnetic interference and vibration, which ultimately will cause phase discontinuities in the time domain. In the same manner as phase noise, phase pops will drive an increase in the BER if proper attention is not given to these important issues.

Table 1 lists the maximum tolerated phase error, without artificial margins, for a given modulation scheme before a decision boundary is crossed by excessive composite system noise.

The fact that 16 QAM is significantly more tolerant than 16 PSK, for example, is also indicated. In addition, as the signal complexity is increased, the error tolerance quickly becomes very small in PSK or QAM.

System Planning

The absolute bottom line to radio link service providers is system availability, which is measured in percents of uptime (or nonavailability, which is measured in percents of downtime). The dominant influence on this performance variable is the weather, namely heavy rain, followed by noise effects caused by the circuitry. Atmospheric effects such as rain can cause a severe attenuation effect on the communication signals. Typically, service providers today are attaining better than a 99.99 percent uptime, which equates to approximately 52 minutes per year of cumulative downtime. The ultimate availability goal is 99.999 percent uptime, which equates to only 5.2 minutes of downtime per year. Fade margin, measured in decibels, is a value given to the system noise budget to insulate the signals against the effect of the weather attenuation. Additional fade margin must be allocated in order to increase the system availability. Usually, additional fade margin is attained by an increase in the transmitter power and antenna gain along with a combination of noise-reduction techniques.

Three key elements must be optimized to assure a well-designed radio link that is relatively resistant to the effects of atmospheric conditions, circuitry noise effects and signal traffic density. The first element is an efficient modulation and transmission system architecture using advanced modulation techniques and transmission protocols to maximize system performance. For example, the use of QAM in place of QPSK might buy some additional fade margin because of the inherent advantages of the phase and amplitude modulation. Forward error correction could be used to accomplish similar margin improvements by systematically eliminating most of the detected bit errors that have managed to slip past the modulator or demodulator.

The second element lies in the system link planning, that is, the physical layout of the network. The availability of a network is heavily dependent upon the weather patterns for the area, primarily in terms of rainfall and fog intensity, and the noise margins allotted to the system. As a result, the link-to-link distances must be optimized through meshed networks to provide alternative signal paths in the likely case of deep fade conditions in the individual links.

The third and probably most important element in the system design is the RF portion of the radio assembly. A byproduct of the link-to-link optimization discussed previously is the noise additions that result from the shorter link distances. Each link will have repeaters that contribute their own degradation to the signal. The net result places more emphasis on obtaining the cleanest signal from the source. A lower phase noise factor in the LO equates to fewer opportunities for bit errors and, therefore, reduces the need for significant error correction or, alternatively, increases the data throughput capacity of the system.

The Modulator/Demodulator Effect

One critical factor in meeting both the performance and cost goals is setting the system specifications accurately. For designs with data rates > 16 kbps, the modulator/demodulator acts as a highpass filter and removes a significant portion of the oscillator’s close-in phase noise. For this reason, the system designer need worry only about the oscillator phase noise from a specified cutoff frequency.

The effective bandwidth of the demodulator is approximately two percent of its data rate. Based on this assumption, Figure 5 shows three transfer characteristics for demodulators with data rates of 32, 128 and 4096 kbps. The modulator will provide a wider bandwidth of close-in filtering for the synthesizer with an increase in the data rate. For example, the use of a 4096 kbps demodulator would provide useful attenuation up to 40 kHz offset. This effect is useful for synthesized technology, particularly YIG-based technology, because the modulator’s noise reduction in the close-in portion of the spectrum diminishes just as the phase-locked-loop-based YIG synthesizer reaches its own open-loop frequency. The region beyond the modulator’s loop natural frequency is where the YIG synthesizer shows a clear advantage with 10 to 25 dB of phase noise improvement over the competing technologies.

Figure 6 shows a tool that allows a direct approach to using integrated synthesizer phase noise values to estimate the degradation in BER for a 64-QAM scheme. The individual traces represent the carrier-to-phase noise power ratio, or phase noise, that is integrated from 40 kHz to 10 MHz offset frequency. The horizontal axis is the carrier-to-noise (C/N) ratio or 10log of the ratio of carrier power to thermal power of the received signal, such as the noise generated by the receiver section components. The vertical axis represents BER. A BER of 10–2 is the threshold for voice communications; a BER of 10–6 is required for data communications, or four orders of magnitude improvement. Since most information is voice and data, the typical BER threshold is a minimum of 10–6.

A technique is described for determining the minimum phase noise performance required to maintain a particular BER value. The modulation scheme assumed is 64 QAM and all other conditions, such as error correction or noise contributions from the low noise amplifier or high power amplifier, are assumed to be identical for this comparison. The offset and integrated phase noise for three commercially available oscillator solutions in the X-band (10.7 GHz) are compared. All phase noise values are open-loop values for a proper comparison of the oscillator properties. The phase noise was integrated from 40 kHz to 10 MHz because the 4096 kbps modulator/demodulator filters a significant portion of the phase noise below 40 kHz offset. Table 2 lists the results of this comparison.

Applying the integrated phase noise value for each technology to the BER vs. C/N graph will yield a BER value at a particular value of C/N, the thermal noise. Conversely, another technique is effective for applying the required BER and system thermal noise to determine the minimum integrated phase noise performance required of the LO. A minimum BER value is chosen that must be met under worst-case conditions. Since 10–6 is the combined voice and data minimum ITU requirement, a value of 10–8 would provide a sufficient margin for a successful design. Next, the C/N value is determined for the radio system. For a 4.096 Mbps data rate and a –80 dBm receive-level incoming signal, a value of 30 dB would be typical. The minimum integrated phase noise required for a BER = 10–8 and C/N = 30 dB is interpolated from the BER vs. C/N graph. For this application in 64 QAM, the integrated phase noise required is 34 dB.

The phase noise comparisons indicate that the VCO would be shy of this requirement by 1 dB, resulting in a BER of approximately 10–7. Most designers would not be comfortable with such a small margin. Both the YIG and DRO technologies would provide ample margin for this application. The key attribute that the YIG solution has to offer over the DRO oscillator is a bandwidth-capable design. A very important point regarding the use of the BER vs. C/N graph is that an increase in the required BER performance places much more importance on the selection of the oscillator performance. For example, to improve the BER performance from 10–6 to 10–9, the system designer would need to improve the oscillator phase noise from 31 to 36 dB or improve the thermal noise from 30 to 35 dB. The antenna size could be increased or the link length shortened to improve the thermal noise. Alternatively, the system engineer may select the YIG or DRO vs. the VCO to improve the oscillator phase noise.

Conclusion

In summary, the demands of the expanding point-to-point and point-to-multipoint radio market are driving a requirement for an increase in signal data rate, a reduced BER and an order of magnitude improvement in the system availability factor. These improvements are taking place while system designers are pushing into the less crowded mm-wave frequencies.

VCOs are suitable for current systems with low data rates and simple modulation but require sophisticated and expensive designs to meet the higher data rate requirements. The DRO’s phase noise capabilities are within the near-term radio requirements but offer little flexibility in terms of bandwidth. The next level of progression in the radio designs now requires significantly improved noise performance and more advanced communication protocols to meet the needs of the limited spectrum.

The only possible path for success to meet these new requirements is a simultaneous and concerted effort by the software designers and system and modem manufacturers to investigate the real system requirements and effect new designs that are capable of meeting the current performance and cost parameters. The end target of required BER performance must be known. From that point, the system variables such as thermal noise or oscillator phase noise can be weighed in order to achieve the desired end target.