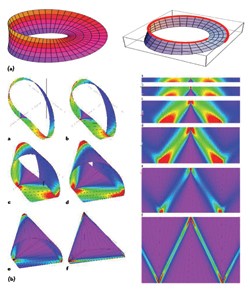
Figure 1 A typical representation of a Möbius strip (a) and computed Möbius strips for different values of width1 (b).
The geometrical phenomenon of anholonomy depends on failure of a quantity to recover its original value, when the parameters on which it depends are varied round a closed circuit. A Möbius strip provides one of the simplest examples of anholonomy, as the normal to the surface of the strip does not return to its original direction even though the radius vector does.1,2 The strip therefore deforms in such a way that its metrical properties are barely changed, some nanostructures have the same elastic properties. A necessary and sufficient condition for a Möbius surface to be developable is that its Gaussian curvature must vanish everywhere. Given a curve with non-vanishing curvature, there exists a unique flat ruled surface (the so-called rectifying developable) on which this curve is a geodesic curve (see Figure 1) is described by1
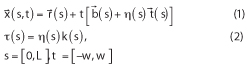
where 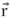 is a parameterization of a strip with r as centerline and of length L and width 2w, where
is a parameterization of a strip with r as centerline and of length L and width 2w, where 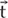 is the unit tangent vector,
is the unit tangent vector, 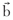 the unit binormal, k the curvature and τ the torsion of the centerline, the parameterized lines s = constant are the generators, which make an angle β= arc[tan(1/η)] with the positive tangent direction.
the unit binormal, k the curvature and τ the torsion of the centerline, the parameterized lines s = constant are the generators, which make an angle β= arc[tan(1/η)] with the positive tangent direction.
The unique properties of Möbius strips, the shape minimizes the deformation energy which is entirely due to bending, can be described by

where D = 2h3E/[3(1-v2)], with 2h the thickness of the strip, and E and v Young’s modulus and Poisson’s ratio of the material.
In this section, a planar Möbius-coupled resonator is described, and the method for miniaturization can be applied to tunable oscillator circuits and memory devices used for receivers, filters, antenna and matching networks.

Figure 2 Photograph of the non planar 3D Möbius dual mode wire resonator (a) and quad-mode (b).
Möbius strip Resonator: Theory
A typical Möbius is a surface with only one side and only one boundary component, the mathematical property of being non-orientable (as shown in Figure 1). A unified system of differential-algebraic equations that describes models of this type was first published in 2007 together with its numerical solution and many technical applications.1-15 The concept of Möbius strips is based on the fact that a signal coupled to a strip shall not encounter any obstruction when travelling around the loop, the loop shall behave like an infinite transmission line, enabling compact high Q-factor resonators. This characteristic enables many radio and microwave applications, including (i) a compact resonator with the resonance frequency which is half that of identically constructed linear coils,2 (ii) a Tesla Coil for global transmission of electricity without wires3, and (iii) high temperature superconductors.4
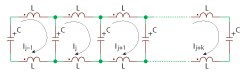
Figure 3 Typical lowpass ladder network consisting of a series of inductances L and capacitances C along the line.
For a typical Möbius strip, one can move along the length of the strip and return to its starting point having traversed the entire length of the strip without ever crossing an edge as shown in Figure 1a. Figure 1b shows computed Möbius strips (coloring changes according to the local bending energy density, from violet for regions of low bending to red for regions of high bending). The left panel shows their 3D shapes for w = 0.1 (a), 0.2 (b), 0.5 (c), 0.8 (d), 1.0 (e) and 1.5 (f), and the right panel the corresponding developments on the plane.1
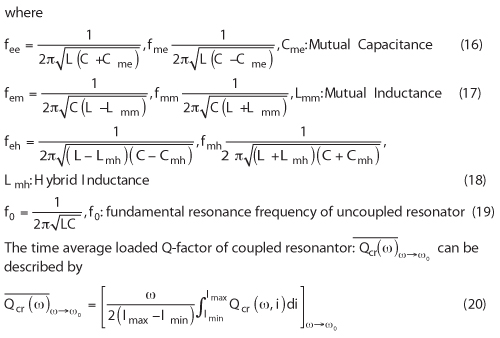
Recent publications describe the Möbius strip resonator2-5 but the surface is a non planar 3D structure (see Figure 2), not suitable for MMIC integration and surface mounted device (SMD) technology applications. Printed resonators are a special class of transmission lines of finite extent with well-defined boundary conditions. The particular interest here is a 1-dimensional printed ring resonator that can be equivalently represented by the simple lumped L-C network shown in Figure 3 (printed resonators are a special class of transmission lines of finite extent with well-defined boundary conditions, the 1-dimensional printed ring resonator can be equivalently represented by the simple lumped L-C network).14 In solving, the electric currents on the resonator can be formulated by a periodic boundary condition of the form described by

where Ik represents the electric current around the nth closed loop on the periodic ladder structure of k-elements. The boundary condition of the general form shown in Equation 4 governs that Ik is a conserved quantity that gives invariance of solutions under a 2π rotation with a definite handedness.
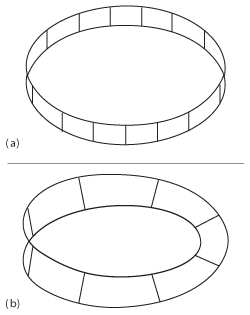
Figure 4 Typical closed loop ring resonator (a) and the Möbius strip resonator (b) a topological transformation of ring resonator into a Möbius strip resonator.15
The 1-dimensional non-dissipative wave equation of LC network shown in Figure 3 for the kth element is given by
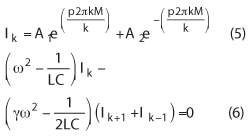
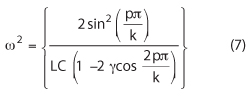
where p is an integer specifying the normal mode, γ is mutual coupling coefficient (mutual inductance ‘M’=2γL) and k is the number of element structure.
From Equations 5 to 7, for even value of k, there are k-1 eigenvalues, including (k-2)/2 degenerate doublets and one singlet. A typical ring resonator, whose Eigen function satisfies Equation 4, defines a distinct inner and outer surface of the ring, shown in Figure 4a. Figure 4b shows a topological transformation resulting in a Möbius strip resonator, whose current dynamics can be formulated by applying twisted boundary condition as

From Equation 8, a simple topological transformation on the resonator ring (4) results in a sign reversal of current (Ij) upon a 2π rotation of the solutions, and a 4π rotation is now required for invariance of the Eigen functions.6-16 Note that the eigenfunctions satisfying the condition for twisted boundary are of the same form as Equation 5 provided that the mode indices are given half-integral values (p = 1/2, 3/2, 5/2,…(k-1)/2) relative to a ring consisting of identical components. The dispersion relation for the Möbius ring is the same as Equation 7; however, the wave-vectors are shifted by

The two distinct topologies shown in Figures 4a and 4b can be considered as a complementary pair related by a single transformation. From Equations 4 and 8, it is evident that there is no additional structure associated with the Möbius ring resonator, since a second topological half-twist transformation on the Möbius resonator leads back to the boundary condition of Equation 4. Their description divides into half-integral and integral normal mode indices. The Eigen functions of the Möbius resonator form an orthogonal basis set, presenting an interesting possibility for the design of metamaterial for the application in tunable oscillators, antenna and filter circuits6. The oscillator’s loaded Q factor QL is given by15
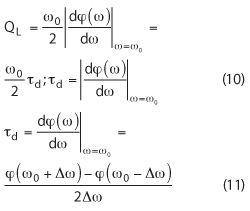
where φ(ω) is the phase of the oscillator’s open loop transfer function at a steady state and τd is the group delay of the resonator.
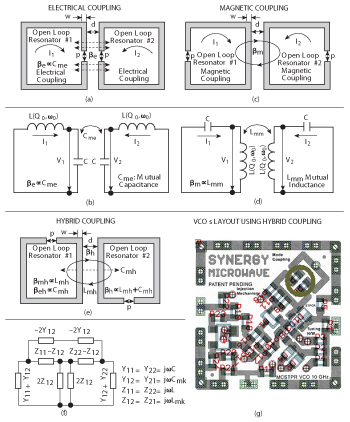
Figure 5 Typical simplified structure of open loop microstrip line coupled resonator networks: (a) electrical coupling, (b) equivalent lumped model of electrical coupling, (c) magnetic coupling, (d) equivalent lumped model of magnetic coupling, (e) hybrid coupling, (f) equivalent lumped model of hybrid coupling and (g) layout of VCO using electric and magnetic coupling.
From Equations 10 and 11, QL is proportional to the group delay; therefore, for low oscillator phase noise application, the design goal is to maximize the group delay of a Möbius strip resonator by incorporating phase-injection techniques. The unique characteristic of a Möbius strip is self-phase-injection properties along the mutually coupled surface of the strips, which enables higher quality factor for a given size of the printed transmission line resonator.
Printed Resonator Based Signal Sources
It is important to achieve a signal source with low phase noise in various applications. The phase noise increases the bit error rate in telecommunication links, degrades stability of the beam in particle accelerators and decreases sensitivity of radars. When high data-rates have to be transferred, as with M-QAM modulation in LTE, LMDS, and fixed frequency point-to-point digital radio and satellite-links, these systems need low phase noise signal sources either free running or phase-locked.
The printed coupled resonator based oscillator offers cost-effective solutions except the poor phase noise performance due to inherent low Q-factor associated with a printed transmission line resonator.17-30 The Q-factor of the coupled planar resonator network can be enhanced by introducing an optimum coupling mechanism (electric/magnetic/hybrid) in conjunction with slow wave propagation, however, the large physical size and mode-jumping restricts the application especially at lower frequencies.30 Figure 5 shows the typical coupling mechanism (electric/magnetic/hybrid) of printed coupled transmission line resonators for tunable oscillator applications.
As described in Figure 5, the coupling dynamics can be characterized by proximity effect through the fringing fields, which exponentially decays outside the region; electric and magnetic field intensity tends to concentrate near the side having maximum field distribution.
The coupling coefficient ‘βj’ depends upon the geometry of the perturbation, and it can be given by
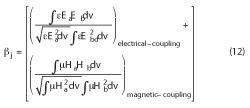
where Ea and Ha are the electric and magnetic fields, respectively, produced by the square loop ring resonator, and Eb and Hb are the corresponding fields due to the perturbation (d≠0) or nearby adjacent resonator (second square loop resonator).
From Equation 12, the first term represents the coupling due to the interaction between the electric ?elds of the resonators and the second term represents the magnetic coupling between the resonators. Depending on the strength of interaction, multi-mode dynamics exist related to electrical, magnetic and hybrid coupling.
The configuration shown in Figure 5a produces an electric coupling, resulting in the electric field being strongest near the open ends, maximizing the numerator of the first term of Equation 12. As depicted in Figure 5b, when the resonators are operating near their first resonant frequency, the pair of resonators interacts mainly through their magnetic field, this is because the magnetic fields are maximum near the center of the resonator opposite to its open ends, maximizing the numerator of the second term of Equation 13. The coupling produced by the two con?gurations (open loop resonator #1 and open loop resonator #2) as shown in Figure 5c are referred to as mixed coupling or hybrid coupling because neither the electric ?elds nor the magnetic ?elds dominate the interaction between the resonators.
The de?nition of ‘βj’ given in Equation 12 involves complex mathematical analysis and is not suited for practical calculation since it requires the knowledge of the electromagnetic ?elds everywhere. A useful alternative expression for ‘βj’ can be obtained from a well known fact in physics: when multiple resonators are coupled to each other they resonate together at different distinct frequencies (fee, fem, feh, fmh) which are in general different from their original resonant frequency f0. Furthermore, these frequencies are associated with corresponding to their normal modes of oscilla-tion of the coupled system (electric/magnetic/hybrid), and their difference increases as the coupling ‘βj’ (βe: electric, βm: magnetic and βh: hybrid) between the resonators increases.30 The main interaction mechanism between resonators is proximity coupling and can be characterized by a coupling coefficient ‘βj’ that depends upon the ratio of coupled energy to stored energy, described by
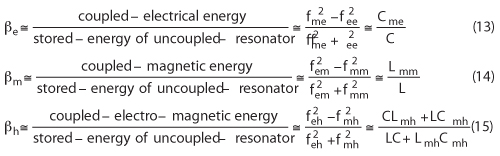
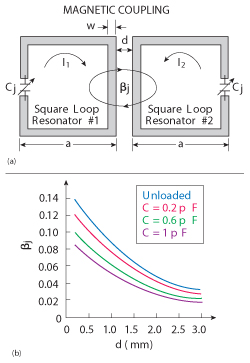
Figure 6 A typical capacitive loaded magnetic coupled square loop resonator layout (a) and plot of magnetic coupling ßj (b).
where Imin and Imax are the minimum and maximum resonator currents associated with the fundamental modes of the coupled resonator networks, the Qcr(ω,i) is the instantaneous quality factor at frequency ω and current i provides an effective means to quantify the Q-multiplier effect when operated in a evanescent-mode coupling conditions, especially in printed coupled resonator based oscillator circuits.
From Equation 20, the loaded quality factor QL of the coupled resonator network is given in terms of unloaded quality factor Q0 as
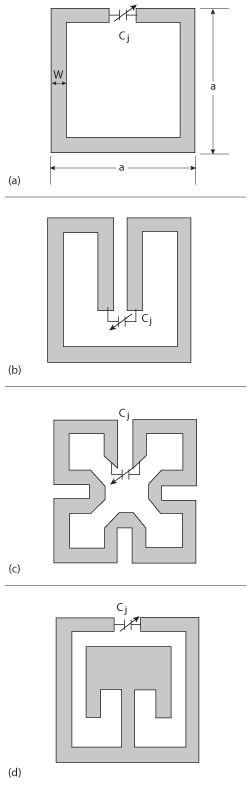
Figure 7 Typical layout of a tunable square open loop resonator: conventional square open loop hairpin resonator (a), folded arms square open loop resonator (b), meander line square open loop resonator (c), dual mode square open loop resonator (d).36
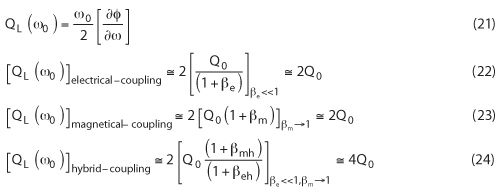
where 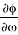 is the rate of change of the phase, and Q0 is the unloaded Q-factor of the uncoupled single open loop microstrip line resonator. From Equations 22 to 24, there is trade-off between improving the Q factor and the permissible attenuation required (which is compensated by active device for oscillation build up).
is the rate of change of the phase, and Q0 is the unloaded Q-factor of the uncoupled single open loop microstrip line resonator. From Equations 22 to 24, there is trade-off between improving the Q factor and the permissible attenuation required (which is compensated by active device for oscillation build up).
The coupling mechanism described in Figure 5 shows improvement in quality factor in comparison to single uncoupled planar resonator but drawback is limited tuning range (less than 1 percent). By introducing tunable capacitor across the open end of uncoupled planar open loop resonator, dynamic unloaded Q-factor can be improved but limited in tuning range (< 25 percent). This is due to minimization of the radiation losses from the open ends of the resonator because of capacitor loading, causing dielectric polarization in the capacitor since most of the electric field resides inside it.31-35 Therefore, a high Q capacitor could actually increase the unloaded quality factor of the whole resonator. This is analogous to the case of dielectric resonators where the fields are constrained to a small volume dielectric with high permittivity and low loss tangent resulting in a high overall Q.37-42
For wideband tunability (> 100 percent tuning), adjacent coupled open loop resonator network is preferred but at the cost of large real estate area. In general, the miniaturization of the open loop resonator reduces its capacity to couple to adjacent structures. This is due to the fact that smaller resonator size represents a smaller volume of electromagnetic interactions between its coupled arms; reason being a smaller size represents a smaller volume of electromagnetic interaction between coupled resonators. The fact that the majority of the electric field that existed in the volume surrounding the open ends of a resonator is now confined to the interior of a capacitor limits its possibility to interact with a neighboring resonator.
It can be seen in Figure 6 that the effect on the magnetic and mixed coupling is less severe than for the electric coupling, where the magnetic coupling coefficient is plotted against the separation between resonators for different loading capacitors.37-42 Figure 6b is a plot of magnetic coupling βj as a function of the distance between resonators for a given capacitive (Cj) loading with resonator physical dimension ω= 2 mm and a = 26 mm, fabricated using Roger RO4003c substrate with a dielectric constant of 3.55 and a thickness of 60 mil.37
The microstrip square open loop resonator is one of the most used structures for multi-mode oscillator resonator applications due to its compact size (a=λ/8). For low phase noise multi-octave band tunability, the loaded quality factor (QL) as described in Equations 21-24 can be maximized by either lowering the value of mutual capacitance (Cm) and inductance (Lm) or maximizing the self-capacitance (C) and inductance (L), therefore, the upper limit of the loaded Q-factor is dependent on the coupling βj (βe: electric, βm: magnetic and βh: hybrid) that can be optimized by controlling the width of the transmission line (w), gap of the open line resonator (p), and spacing between the two open line resonators (d).43-48 For low phase noise tunable oscillators, the coupling coefficient βj should be dynamically tuned over the operating frequency band. However, dynamic controlling and tuning of the parameters (w, p, a and d) as shown in Figure 5 at high frequency is a challenging task. The alternative tuning mechanism is capacitive loading by incorporating tuning diodes.31-37
Figure 7 shows a typical tunable square open loop resonator in compact size (λ/8 by λ/8) for applications in oscillator circuits. As shown in Figure 7c, the goal is to minimize the real estate area by using a meander line into inner part of the resonator. To optimize the geometry of the coupled resonator, they are excited with a pair of loosely coupled feed lines to obtain a transmission parameter S21(ω) from which the two resonant frequencies f1 and f2 can be obtained for a given geometry and values of d between resonators. The resonator shown in Figure 7d offers compact size and exhibits two independent modes (dual-modes), the coupling between them can be optimized by the geometry of the inner structure. This tunable dual-mode resonator can then function as two independent tunable resonators providing an immediate size reduction of 50 percent.
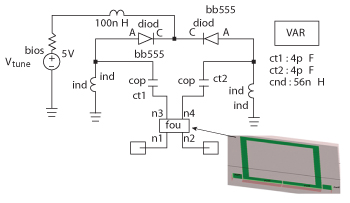
Figure 8 A typical setup for carrying out the measurement of the transmission coefficient S21 (ω) for analyzing the coupling characteristics of the varactor loaded tunable open loop resonator.
Figure 8 shows the typical setup used for measurement of the S21(ω) for deriving the coupling characteristics of the tunable open loop resonator loaded with the varactor diode. The parameter of interest is the transmission coefficient S21(ω), where the resonant frequencies are manifested as peaks of maximum transmission between ports.
Figure 9 shows CAD simulated (Ansoft Designer) plot of the varactor loaded open square loop printed resonator with ω = 2 mm and a = 26 mm, fabricated using Roger RO4003c substrate with a dielectric constant of 3.55 and a thickness of 60 mil (1.524 mm).37-43 As shown in Figure 9, the first resonant frequency is shifted down with different values of C, whereas the second resonance frequency remains at the same location. Nevertheless, as varactor diode capacitance increases beyond a certain value (for example, 1.4 pF), a couple of frequencies where the transmission coefficient S21 is zero appear between the first and second resonant frequencies, which is observed in Figure 9 for C = 2 pF. As shown in Figure 9, the physical size of the resonator (ω = 2 mm and a = 26 mm) is kept constant while C is varied causing a shift in the first resonant frequency. This frequency shift can be capitalized into miniaturization if we let the size of the resonator vary but at the cost of increase in insertion loss. A novel Möbius strip resonator can overcome these problems and offers promising and cost-effective solutions. The concept of the Möbius strips is based on the fact that a signal coupled to a strip shall not encounter any obstruction when travelling around the loop; enabling compact high Q-factor resonators.
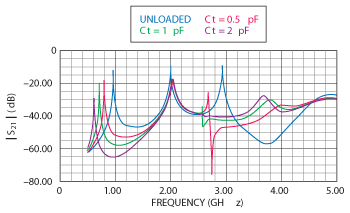
Figure 9 A CAD simulated (Ansoft Designer) plot of S21 (ω) of a varactor loaded open loop resonator for different capacitance values.
Möbius-Coupled Evanescent-Mode Resonator Oscillator
A novel mode-coupled self-injection locked oscillator is developed in response to improve the insertion loss and loaded Q-factor of the printed resonator network shown in Figure 7 for the application in modern communication systems.
Figures 10 to 12 show the typical block diagram, layout and measured phase noise plot, respectively, of the 10.2 GHz oscillator using a SiGe HBT active device fabricated on Rogers substrate material with a dielectric constant of 2.2 and thickness of 20 mils (microstripline/stripline) for the validation of the approach. The prototype oscillator circuit shown in Figure 11 works at DC bias of 10 V and 30 mA, measured output power exceeds +5 dBm. The phase noise plot shown in Figure 12 exhibits hump and dip between 100 kHz and 10 MHz offset from the carrier, possibly due to the resonator mode-jumping and mode-degeneration phenomena. By incorporating mode-injection-locking, mode-jumping can be suppressed and stable oscillation can be achieved.
Figure 13 shows the typical block diagram of mode-injection-locked Möbius strip resonator VCO topology that can offer integration and low cost solutions. Figure 14 shows the typical layout of 10 GHz Möbius resonator based oscillator for building low phase noise signal source for radar applications.
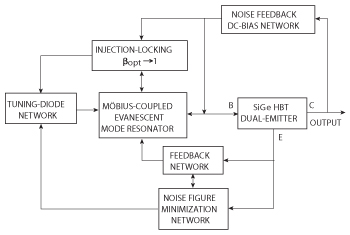
Figure 10 A typical block diagram of an X-Band Möbius-coupled evanescent mode resonator (MCEMR) oscillator.
Figure 15 shows the measured phase noise plot (–110 dBc/Hz at 10 kHz offset) from the carrier frequency of 10 GHz offers significant improvement in figure of merit (FOM) for a given phase noise, tuning range and power consumption. A spot phase noise number is difficult to compare, unless it is compared at the same frequency offset from the carrier and the same carrier frequency for a given tuning range and output power. Comparing oscillators operating at different frequencies, tuning range and output power levels, a FOM with a single number has long been desired.
In order to make a fair comparison of the performances of VCOs at different operating frequencies, a FOM is used. The FOM in and power-frequency tuning-normalized (PFTN) in dB are defined as49
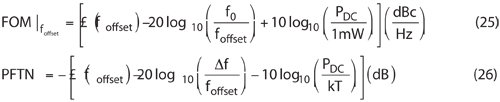
where f0 is the oscillation frequency, £(foffset) is the phase-noise at the offset frequency foffset, k is the Boltzmann constant, Δf =fmax -fmin is tuning range, T is temperature in Kelvin, and PDC is the total consumed DC power in milli-watts.
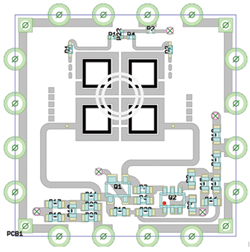
Figure 11 Layout of 10.2 GHz MCEMR VCO (0.9" × 0.9" × 0.2").
Larger |FOM| and PFTN(dB) values relate to superior oscillators. From Equations 25 and 26, the FOM for integrated phase noise in dBc from 1 kHz to 1 MHz can be given by
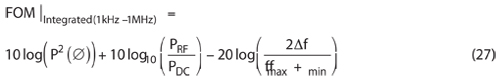
where Δf = fmax – fmin;fmax = maximum oscillation frequency; fmin = minimum oscillation frequency; P2(ø) = integrated phase noise from 1 kHz to 1 MHz; PRF = signal output power averaged over frequency; PDC = DC power consumption of the oscillator.

Figure 12 Measured phase noise plot of 10.2 GHz MCEMR VCO.
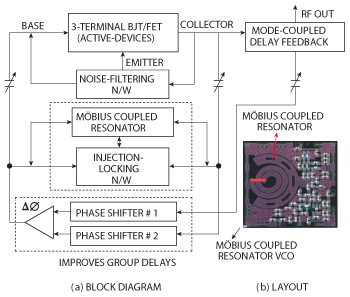
Figure 13 Shows the typical block diagram 10 GHz Möbius coupled resonator VCOs using a SiGe HBT active device, built on 20 mil substrate material.
As shown in Figure 14, the frequency is set at the fundamental resonance of Möbius-coupled evanescent mode resonator (MCEMR) and can be electrically tuned by using varactor network (tuning voltages of 1 to 24 VDC enable variations in the center frequency by ±400 MHz to compensate for frequency drift in phase-locked systems).
Figure 15 shows the measured phase noise plot of 10 GHz MCEMR VCO. The measured phase noise at 10 kHz offset is better than –110 dBc/Hz, validates the tuning capability without degrading the phase noise performance in SMD packaged version. From Equation 25, the measured FOM at 1 MHz is –195.9 dBc/Hz for hybrid coupled resonator, –202.9 dBc/Hz for Möbius coupled resonator, and –204.9 dBc/Hz for Mode-locked Möbius coupled resonator network; with power consumption of 160 mW (Vcc=5 V, Ic=32 mA). The DC-RF conversion efficiency is 1.2 percent for hybrid coupled resonator, 1.3 percent for Möbius coupled resonator, 1.7 percent for mode-locked Möbius coupled resonator network; with DC power consumption of 160 mW (Vcc=5 V, Ic=32 mA).
Synthesized Frequency Sources using Möbius Coupled Resonator (MCPR) VCOs
Figure 16 shows a 2 to 8 GHz broadband synthesizer using wideband (2 to 8 GHz) tunable MCPR VCO (layout of VCO is shown in Figure 16b, built on 22 mil substrate with a dielectric constant of 2.2). It offers a viable cost-effective solution for expensive YIG resonator oscillator with less susceptibility to thermal drift, vibrations and microphonics.
As shown in Figure 16a, the synthesizer circuit draws typically 200 mA current from a 5 V supply, uses multi-band/multi-mode MCPR VCO (operating at 5 V, 32 mA) resulting in a low-cost power-efficient configurable synthesizer. The typical measured phase and the mode stabilized synthesizer circuit as illustrated is typically better than –112 dBc/Hz at 10 kHz offset for 2 to 8 GHz operations. The reported synthesizer module shown in Figure 16a offers wide bandwidths with excellent performance in terms of phase noise, harmonics (> –20 dBc), settling time (< 1 millisecond), and sideband spurious content (> –60 dBc), with low power consumption in compact size (1 × 1 × 0.2 inches) built on 22 mil substrate material with a dielectric constant of 2.2 for the validation of the new approach. The synthesizer using tunable oscillators with Möbius strip resonators yields compact VCOs with excellent phase-noise performance and in configurations that can be readily adapted to modern RF integrated circuit (RFIC) and MMIC semiconductor manufacturing processes.
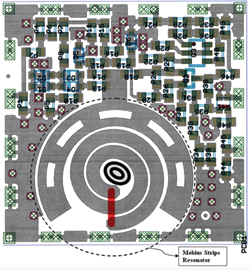
Figure 14 Layout of 10 GHz oscillator (depicts the phase-injection-mode-locked) Möbius strips resonator (22 mil substrate thickness with 2.22 dielectric constant, 0.7" × 0.75" × 0.18").
Real Time Signal Retention Device
The signal retention characteristics of Möbius coupled strip resonators are useful in RF and microwave applications, including radio astronomy, medical fields and software driven radios. Conventionally, high Q cavity echo box is used in radar testing to retain the input signals but this technique has bandwidth limitation.4 The frequency memory loop (FML) technique is used in military electronics for retention of signals; this is an expensive solution with considerable digital signal processing and invariably noisy and bandwidth limited.11 The Möbius strip configuration (back to back coplanar waveguide) reported here shows how the characteristic is non-resonant unlike open or shorted transmission lines, which have the ability to store broadband frequencies in a compact size.
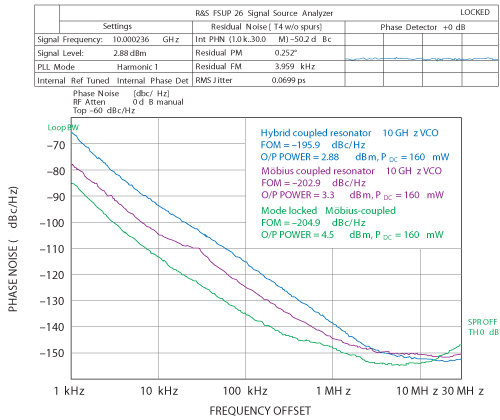
Figure 15 Measured phase noise plot of the 10 GHz oscillator using: hybrid coupled resonator, Möbius coupled resonator, mode-locked Möbius coupled resonator network.
A typical back to back coplanar waveguide (CPW) in the form of a Möbius strip was constructed which resulted in an infinite transmission line capable of retaining a large bandwidth of frequencies that can be useful for real time signal retention device (RTRD).14 By providing a Möbius twist to CPW, a continuous phase change was reported instead of abrupt phase change by using shorting pins between two parallel transmission lines. It is observed that the device retains the injected signal in time domain over a broadband of frequencies. The signal can also be a pulsed signal as in ultrawideband (UWB) or a modulated microwave signal to retain transient signals encountered in radio astronomy, medical applications and many others. Figure 17 shows a photograph of the prototype Möbius strips for the application as signal retention device.
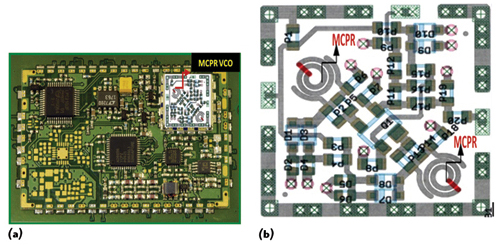
Figure 16 Typical PCB layout of 2 to 8 GHz configurable synthesizer module (a) and layout of a 2 to 8 GHz Möbius coupled planar resonator VCO (b).
As shown in Figure 17, the central partition plane acts more as a separation between the top and bottom layers to prevent coupling. The spacing between the central conductor and ground plane on the coplanar side is much smaller than the thickness of the substrate leading to maximum field confinement on the surface. There exists a discontinuity in the partition ground planes. This characteristic is taken into account for futuristic study while developing the mathematical model for the infinite strip. Ground looping was avoided to realize the infinite transmission line at the cost of generation of higher order modes.

Figure 17 A prototype Möbius strip with SMA connectors.14

Figure 18 Agilent FieldFox RF analyzer N9912 with the device connected — the Smith Chart indicates the broadband coupling of signal into the device.14
Agilent FieldFox RF Analyzer N9912 was used to test the proof of concept.17-19 This instrument has a single port S-parameter testing capability (VNA) along with cable testing facility; in addition it contains a spectrum analyzer up to 6 GHz. The test setup is as shown in Figure 18. First, the return loss was tested from 2 to 6 GHz with one of the ports terminated with 50 ohms. It was observed that the device has a return loss between 8 and 20 dB over the frequency range. This indicates that the device is exhibiting broadband behavior and the signal is getting coupled to it. In other words, the continuous central conductor is getting excited over a broadband of frequencies. The Smith Chart display shows the excitation of the signal to the continuous center conductor of the device over a bandwidth of 4 GHz. In this way, the device exhibits an infinite transmission line. The return loss response of more than 10 dB indicates that the energy is efficiently coupled to the device over a bandwidth of 4 GHz.

Figure 19 The VNA was switched to cable and antenna testing mode to check the delay response in real time of the Möbius strips shown in Figure 16.14
The VNA shown in Figure 18 was switched to cable and antenna testing mode to check the delay response in real time (see Figure 19). In this way the retention of the signal can be tested. The instrument converts the measured frequency response into time domain response by performing inverse fast Fourier Transform (IFFT). The measured results as expected are a gradual decay of the signal after every transit around the loop. Thus testing of the device has confirmed the retention of the signal in real time over broadband of microwave frequencies. The total span time is around 200 milliseconds. The physical length of the loop is 30 cm. The markers as indicated are at 0.72, 0.89, 0.98, 1.05, 1.13 and 1.46 m. This indicates multiple transit of the signal around the loop. It also shows the broadband retention characteristics since it is derived from the frequency response of the device. To verify the effect of signal retention device (SRD) performance, different loop lengths (45, 60 and 75 cm) was made and the testing is reported in Big Loop. The performance was similar to 30 cm SRD with edge coupled input.
The signal travels twice around the loop before arriving at the feeding point, the first signal is at twice the length of the loop which is at 72 cm. The decay of the signal over the time indicates the coupling of the power at the output port along with the losses, considering the radiation losses are minimal. This behavior calls for extensive mathematical modeling of the device. The unusual behavior could be due to the magnetic field coupling between the top and bottom layers. This will result in a distributed mutual inductance between the layers. This characteristic is similar to non-inductive resistor design.9 The interesting frequency response of the device calls for rigorous three dimensional mathematical modeling and analysis using Maxwell’s equations and shall lead to considerable research in the field of signal retention.
The Möbius co-planar structure proposed in Figure 17 for signal retention is analog by nature and is an economical solution for signal retention.14 It is observed that the device retains the injected signal in time domain over a broadband of frequencies. The signal can also be a pulsed signal as in UWB or a modulated microwave signal. It can retain transient signals encountered in radio astronomy, medical applications and many others. The device is truly analog and can improve the performance of an analog to digital converter (ADC). One can use a lower speed digital signal processing (DSP) since one has the same signal available for a considerable duration of time in a repetitive manner. It is also feasible to fabricate the device using rapid prototyping MEMS applications. This will open up many more exciting millimeter wave applications such as microwave sensors for remote sensing and detection of hidden objects, to find concealed explosives and hazardous chemicals.
Möbius Coupled Resonator Strips: Discussion
Abnormal Behavior: Unlike any resonant structure, the return loss was observed to be around the center of the Smith Chart, which is non-resonant behavior from 2 MHz to 6 GHz. Based on our observation, any loop was exhibiting resonant nature and the response was touching the outer edge of the Smith Chart, in other words the input impedance moved from short to open.
Testing of Loop: A CPW guide with quadrature coupler was made into a simple loop and tested for performance. The purpose of this was to isolate the effect of the twist. It was found that the loop behaves like a resonant circuit with multiple frequencies and S11 touched the 0 dBm axis.
Video Recording: The Yagi antenna was connected to the spectrum analyzer with and without the signal retention device. This is to check whether the device retains pulsed RF waveforms. A cell phone was kept nearby and the filming was done using a digital camera. The uplink from the cell phone is a burst signal. There is a repetitive appearance of the signal on activating the cell phone when the device was connected indicating the retention of burst signal.
Conclusion
The signal retention device developed here has the ability to store a very broad band of frequencies. It also has the ability to store a transient signal for delayed analysis. This property of the device is extremely useful in many applications including radio astronomy, medical fields and software driven radios, real-time retention of signals for signal processing, and frequency memory loop in electronic warfare. This device will be less ‘noisy’ compared to digital storage devices, can be very useful in software driven radios and help in soft handover from one system to another and other applications.
References
- E.L. Starostin and G.H.M. van der Heijden, “The shape of a Möbius Strip,” Nature Materials 6 (8): 563–7. doi: 10.1038/nmat1929.PMID 17632519, (2007).
- J.M. Pond, “Möbius Dual Mode Resonators and Bandpass Filter,” IEEE Transactions of MTT, Vol. 48, No. 12, December 2000, pp 2465-2471.
- J.M. Pond, S. Liu, and N. Newman, “Bandpass Filters Using Dual-Mode and Quad-Mode Möbius Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. 49, December 2001, pp. 2363-2368.
- I.G. Wilson, C.W. Shramm and J.P. Kinzer, “High Q Resonant Cavities for Microwave Testing,” Bell System Technical Journal,No. 5, doi:10.1364/OPEX.13.001515, March 2005, pp. 1515-1530.
- V. Honkote, “Capacitive Load Balancing for Möbius Implementation of Standing Wave Oscillator,” 52nd IEEE MWSCAS, 2009, pp. 232-235.
- A.J. Hoffman et al., “Negative Refraction in Semiconductor Metamaterials,”Nature Materials6, October 2007, pp. 946-950.
- J.F. Gravel and J.S. Wight, “On the Conception and Analysis of a 12 GHz Push-Push Phase Locked DRO,” IEEE Transactions on MTT, Vol. 54, No. 1, January 2006, pp. 153-159.
- U.L. Rohde and A.K. Poddar, “Miniaturized VCOs Arm Configurable Synthesizers,” IEEE IMS Digest, June 2009.
- N. Tesla, “Coil for Electromagnet,” US Patent 512340, January 9, 1894.
- R. Pérez-Enríquez, “A Structural Parameter for High Tc Superconductivity from an Octahedral Möbius Strip in BaCuO :123 type Perovskites,” Rev Mex Fis v.48 Supplement 1, 2002, p. 262.
- Development in FML and Miniature Millimeter Devices, Watkins Johnson, Tech Note, Vol. 1, No. 2, March 1974.
- U.L. Rohde and A.K. Poddar, “DRO Drops Phase-noise Levels,” Microwaves RF, February 2013, pp. 80-84.
- U.L. Rohde, A.K. Poddar and A. Apte, “Phase Noise Measurement and its Limitations,” Microwave Journal, April 2013.
- A.K. Poddar, U.L. Rohde, D. Sundarrajan, “Real Time Signal Retention Device using Co-planar Waveguide (CPW) as Möbius Strip,” 2013 IEEE MTT-S Digest, June 2013, pp. 1-3.
- A.K. Poddar and U.L. Rohde, “A Novel Evanescent-Mode Möbius-Coupled Resonator Oscillators,” IEEE Joint UFFC Symposia with European Frequency and Time Forum (EFTF) and Piezo Response Force Microscopy, July 21-25, 2013.
- Anritsu Application Note, “Time Domain Reflectometry using Vector Network Analyzers.”
- Agilent Application Note, Time Domain Analysis using a Network Analyzer, January 6, 2012, 1287-1312.
- Agilent “Time Domain Analysis Using a Network Analyzer,” Literature Number 5989-5723EN, May 2012.
- A.K. Poddar, U.L. Rohde and A.S. Daryoush, “Integrated Production of Self Injection Locked Self Phase Loop Locked Opto-electronic Oscillators,” US Patent Application No. 13/760767,(filed on Feb 6, 2013).
- A.K. Poddar, U.L. Rohde and A.S. Daryoush, “Self Injection Locked Phase Locked Looped Optoelectronic Oscillator,” US Patent Application No. 61/746, 919,(filed on December 28, 2012).
- W. Heinrich, “Comments on “Internal Impedance of Conductors of Rectangular Cross Section,” IEEE Transactions on MTT, Vol. 49, March 2001, pp. 580-581.
- W. Heinrich, “Full-wave Analysis of Conductor Losses on MMIC Transmission Lines,” IEEE Transactions on Microwave Theory and Techniques, Vol. 38, October 1990, pp. 1468-1472.
- W. Heinrich, “Quasi-TEM Description of MMIC Coplanar Lines including Conductor Loss Effects,” IEEE Transactions on Microwave Theory and Techniques, Vol. 41, January 1993, pp. 45-52.
- W. Heinrich and H. Kuhnert, “Coplanar SiGe VCO MMIC beyond 20 GHz,” Silicon Monolithic Integrated Circuits in RF Systems 2001 Tropical Meeting Digest, 2001, pp. 231-233.
- F. Schnieder and W. Heinrich, “Model of Thin-film Microstrip Line for Circuit Design,” IEEE Transactions on MTT, Vol. 49, 2001, pp. 104-110.
- M. Rudolph and W. Heinrich, “Assessment of Power-transistor Package Models: Distributed Versus Lumped Approach,” Microwave Integrated Circuits Conference (EuMIC), 2010, pp. 86-89.
- M. Buchta and W. Heinrich, “On the Equivalence between Cylindrical and Rectangular Via-holes in Electromagnetic Modeling,” European Microwave Conference, EuMc=C 2007, pp. 142-145.
- M. Hossain, A. Kravetsm U. Pursche, C. Meliani and W. Heinrich, “A Low Voltage 24 GHz VCO in 130nm CMOS for Localization Purpose in Sensor Networks,” 7th German Microwave Conference (GeMiC), 2012, pp. 1-4.
- S. Kuhn and W. Heinrich, “GaN Large-signal Oscillator Design using Auxiliary Generator Measurements,” German Microwave Conference (GeMiC), 2010, pp. 110-113.
- A.K. Poddar and U.L. Rohde, “A Novel Evanescent-Mode Mobius-Coupled Resonator Oscillators,” IEEE joint UFFC Symposia with European Frequency and Time Forum (EFTF) and Piezo Response Force Microscopy, July 21-25, 2013.
- J.S. Hong and M.J. Lancaster, “Theory and Experiment of Novel Microstrip Slow-wave Open-loop Resonator Filters,” IEEE Transactions on MTT, Vol. 45, December 1997, pp. 2358-2365.
- M. Sagawa, K. Takahashi and M. Makimoto, “Miniaturized Hairpin Resonator Filters and Their Application to Receiver Front-end MIC,” IEEE Transactions on Microwave Theory and Techniques, Vol. 37, December 1989, pp. 1991-1997.
- F. Rouchaud, V. Madrangeas, M. Aubourg, P. Guillon, B. Theron and M. Maignan, “New Classes of Microstrip Resonators for HTS Microwave Filters Applications,” IEEE MTT-S International Microwave Symposium Digest, 1998, pp. 1023-1026.
- J.T. Kuo, M.J. Maa and P.H. Lu, “A Microstrip Elliptic Function Filter with Compact Miniaturized Hairpin Resonators,” IEEE Microwave and Guided Wave Letters, Vol. 10, March 2000, pp. 94-95.
- U.L. Rohde and A.K. Poddar, “STPCR Offers Integrable Alternatives Of DRO,” 2008 IEEE MTT-S, June 15-20, 2008, Atlanta, GA, pp. 233-236.
- R.J. Cameron, C.M. Kudsia and R.R. Mansour, “Microwave Filters for Communication Systems,” Fundamentals, Design, and Applications, 2007, John Wiley & Sons Inc.
- L.M. Ledezma, “A Study on the Miniaturization of Microstrip Square Open Loop Resonators,” MS Thesis 2011, USF.
- J. Hong and M. Lancaster, Microstrip Filters for RF/Microwave Applications,John Wiley and Sons, 2001.
- F.X. Sinnesbichler, B. Hautz and G.R. Olbrich, “A Si/SiGe HBT Dielectric Resonator Push-push Oscillator at 58 GHz,” IEEE Microwave and Guided Wave Letters, Vol. 10, April 2000, pp. 145-147.
- L.H. Hsieh and K. Chang, “Slow-wave Bandpass Filters using Ring or Stepped Impedance Hairpin Resonators,” IEEE Transactions on MTT, Vol. 50, July 2002, pp. 1795-1800.
- T.Y. Yun and K. Chang, “Analysis and Optimization of a Phase Shifter Controlled by a Piezoelectric Transducer,” IEEE Transactions on MTT, Vol. 50, January 2002, pp. 105-111.
- Y.M. Poplavko, Y.V. Prokopenko, V.I. Molchanov and A. Dogan, “Frequency-tunable Microwave Dielectric Resonator,” IEEE Transactions on MTT, Vol. 49, June 2001, pp. 1020-1026.
- H. Yabuki, M. Sagawa and M. Makimoto, “Voltage Controlled Push-push Oscillators using Miniaturized Hairpin Resonators,” IEEE MTT-S IMS Symposium Digest, 1991, pp. 1175-1178.
- M. Sagawa, K. Takahashi and M. Makimoto, “Miniaturized Hairpin Resonator Filters and Their Application to Receiver Front-end MIC,” IEEE Transactions on Microwave Theory and Techniques, Vol. 37, December 1989, pp. 1991-1997.
- B.C. Wadell, Transmission Line Design Handbook, MA: Artech House, 1991, pp. 321.
- M. Kirschning, R.H. Jansen and N.H.L. Koster, “Measurement and Computer Aided Modeling of Microstrip Discontinuities by an Improved Resonator Method,” IEEE MTT-S International Microwave Symposium Digest, 1983, pp. 495-497.
- S.Y. Lee and C.M. Tsai, “New Cross-coupled Filter Design using Improved Hairpin Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. 48, December 2000, pp. 2482- 2490.
- C.M. Tsai, S.Y. Lee and C.C. Tsai, “Hairpin Filters with Tunable Transmission Zeros,” IEEE MTT-S International Microwave Symposium Digest,2001, pp. 2175-2178.
- D. Ham and A. Hajimiri, “Concepts and Methods in Optimization of Integrated LC VCOs,” IEEE Journal of Solid-State Circuits, Vol. 36, No. 6, June 2001, pp. 896-909.
