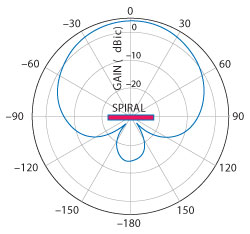
Figure 1 Typical spiral radiation pattern.
This article describes a planar spiral antenna structure and its electrical characteristics. To avoid complex mathematical discussions that may be unnecessary for general readers, planar spiral design techniques are described in qualitative rather than quantitative terms. The design discussions appear in progressively important order, so that readers can develop insights into critical reasoning for using or designing spiral antennas. In addition, this article presents limitations of spiral antennas to provide system designers performance tradeoffs when they consider using spiral antennas in their system designs.
The most widely used spiral antenna type is the two-armed planar spiral with metal cavity housing. Other spiral types are usually more complex, uneconomical and unpopular and therefore are not discussed here. For example, a four-armed spiral antenna is much more challenging to build than the two-armed spiral design. Yet, the four-armed spiral’s performance may only be slightly better than the two-armed one. Thus the benefits of the four-armed spiral may not warrant the added cost, size and weight of the four-armed spiral.
The two-armed planar spiral antenna, or spiral, has two conductor arms that wind from the center of the spiral to gradually a larger radius in multiple turns. The number of winding turns has the effect of tight or loose spiral structures. The tight spiral tends to have more frequency independent radiation pattern behaviors. The expected effect of the numbers of winding turns has the least impact to overall spiral performance, so long as the spiral is not too loose. Winding turns equal to or greater than three are typically sufficient. Conductor arm shapes are designed such that one arm, when rotated 180°, is the same as the other arm. This guarantees that the spiral structure is rotationally symmetrical, at least across 0° and 180° on a given plane cut.
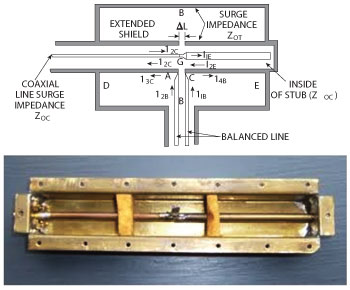
Figure 2 Typical Marchand balun (N. Marchand, "Transmission Line Conversion Transformers," Electronics, Vol. 17, Dec. 1944, pp. 142–145).
There are two possible radiation modes for a two-armed spiral. Mode 1 is defined as a broad amplitude pattern beam with its peak normal to the spiral plane, shown in Figure 1. Mode 1 phase has a one-cycle phase (hence “Mode 1”) from 0° to 360° around the spiral winding. This is the desired radiation mode for most applications. On the other hand, Mode 2 has a split amplitude pattern beam, with a null normal to the spiral plane. Mode 2 phase has a 2:1 phase cycle from 0° to 720° phase around the spiral winding. Mode 2 is rarely used, except in special applications requiring sophisticated beamforming.
It is important to note that the spiral is typically fed by an RF coaxial connector, which has its center conductor unbalanced with its outer conductor. Unbalanced current feeding the spiral can simultaneously excite both Mode 1 and Mode 2 radiation patterns, which is highly undesirable.
Balun Design for Spiral Antenna
To overcome this, a balun circuit is needed as part of the overall spiral antenna design to convert the unbalanced coaxial mode current to the balanced mode current that connects to the spiral arms in the center.
Since the spiral antenna’s radiation properties are identical to its reception properties (by reciprocity principles), only spiral radiation is described without loss of generality. If the balun is properly designed, then the spiral radiates the desirable Mode 1 symmetric pattern characteristics in a given azimuth or elevation plane. This is an extremely important performance factor because spiral amplitude patterns are critically used for providing system Angle of Arrival (AoA) performance. However, if the balun is poorly designed, the spiral experiences undesirable performance, such as beam squinting, high axial ratio and pattern nulls. These culprits severely degrade system performance. Therefore, the balun design is one of the most critical elements for a high-performance spiral in an Electronic Warfare (EW) or Electronic Support Measure (ESM) systems. Some commonly used balun designs in the antenna industry are the 10:1 band Marchand balun, shown in Figure 2, and the 40:1 band microstrip taper balun, shown in Figure 3. The Marchand balun is based on RF circuit symmetry, which is consistent with the spiral structure’s rotational symmetry. As a result, the Marchand balun is usually the best choice for high-performance spirals, at the expense of some design complexities that lead to higher cost and more weight.

Figure 3 Typical taper balun.
On the other hand, the microstrip taper balun is based on the smooth and gradual transition of an unbalanced mode microstrip line at the connector end to a balanced, equal width parallel strip mode at the spiral center. If the transition length is reasonably sufficient – for instance at least a 3/8 waveguide length – then the taper balun can yield reasonable spiral performance at a much lower cost. The benefit of the taper balun is that low-cost, mass producible printed circuit designs can be realized for high-volume manufacturing.
Equi-angular or Archimedean Spirals
The spiral antenna has two common designs; one is the equi-angular spiral and the other is the Archimedean spiral. The equi-angular spiral design, shown in Figure 4, has both the radius and the line-width increasing exponentially with the angles. In this way, the spiral structure is truly self-scalable and self-complementary. Self-scalable means that after the structure dimensions are scaled, the scaled dimensions look exactly like a portion of the original dimension. Self-complementary means that after the two-arm conductors are interchanged with the air space between the arms, the interchanged structure looks exactly like the original structure rotated 90°. This allows near frequency-independent performance. When the frequency changes, the geometry dimensions per wavelength remain nearly the same, thereby preserving the spiral’s electrical characteristics.

Figure 4 Typical two-armed equi-angular spiral.
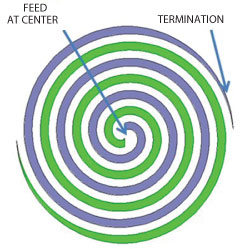
Figure 5 Typical two-armed Archimedean spiral.
On the other hand, the Archimedean spiral, shown in Figure 5, has its radius increasing linearly with angles. Such a radius restricts the line width to be constant with the angles, which avoids short circuiting other parts of the spiral arms. Although the Archimedean spiral geometry is not exactly self-scalable and self-complementary, due to its constant line width, its arm radius is still partially self-scalable and self-complementary. Thus, for all practical purposes, the Archimedean spiral is considered near frequency independent, if the spiral arm line width is sufficiently small. Although the Archimedean spiral performance over fine frequency increments is not as uniform as the equi-angular spiral, this is usually not a serious problem. This is because modern EW or ESM systems typically allow antenna calibration at fine frequency increments to overcome such frequency variations.
Active Region
Any practical antenna must have a finite size to meet certain system size requirements. As mentioned, the spiral arm radius increases with angles. At some radius, this spiral arm must be truncated. This truncation sets the low-frequency limit for the spiral performance. As a result, this truncation becomes a very important design parameter.
As mentioned, the balun feeding the two spiral arms at the spiral center is a balanced current pair – one arm is 180° out of phase with the other arm. According to Burdine’s radiation band theory, little or no radiation takes place for this pair of balanced currents at or near the spiral center. However, as the spiral arm increases, the differential phase between two adjacent arms progressively deviates from 180°. At some point along the spiral arm, significant radiation takes place, where the phase deviation approaches 0°. In other words, the adjacent currents at this location are in phase. This is the so-called “Active Region” where the spiral currents are free to radiate without counter-restricting each other. Conversely, where the current is balanced along the arms before approaching the active region, such as at or near the spiral center, little radiation takes place. This is the so-called “Inactive Region.” From simple geometry calculations, the active region is where the spiral circumference is one wavelength (one λ long).
Truncation Effects
The truncation of the spiral arm inherently excites reflection currents at the truncation end of the arm. These reflection currents travel in the opposite direction toward the spiral center and thereby radiate with the opposite sense of circular polarization (CP). When this opposite sense CP radiation combines with the normal sense CP radiation, the spiral’s axial ratio performance will be severely degraded.
To compensate for such truncation effects, designers use a larger spiral diameter, typically 20 percent more, to move the active region away from the truncation ends. The current loses most of its amplitude (that is RF power) to the far field after the active region and only little RF power remains at the truncation. As a result, little reflection takes place at the truncation, as if the truncation is not there. The following formula shows the minimum diameter size for designing a spiral antenna:

The second most important design parameter is to ensure the spiral circumference is at least one λ at the lowest frequency.
Absorptive Termination
When size is a constraint – such as tight array spacing in a broadband interferometer system for ambiguity rejection at the highest frequency – designers may not have the luxury to choose the spiral diameter using the given equation for lowest frequency. In this case, some termination techniques are needed to reduce the reflection current for the undersized spirals.
One simple way to terminate the spiral is to put absorptive RF materials on the spiral’s outer few rings. As current passes through the added absorptive materials, some of the current’s RF power is absorbed and most of the RF power still radiates into the far field. This is a very effective technique for maintaining the spiral’s axial ratio and input impedance performance, at the expense of slightly lower gain efficiency. The typical gain efficiency loss is on the order of one to two dB, which may be a reasonable compromise between size and performance. Some designers use RF chip resistors as absorptive termination. Resistance values from 120 to 200 Ω are typical, depending on the actual spiral line width to line spacing ratio.
Reactive Termination
Another technique is to use less-absorptive dielectric loading materials to slow the current’s traveling speed, which is called reactive termination. Some less-absorptive dielectric materials can be added on the outer few rings of the spiral. As current passes through these dielectric materials, the spiral effectively appears electrically larger. As a result, this mitigates truncation effects. This technique is less effective because too much dielectric loading can introduce adverse side effects such as higher order spiral radiation modes, which significantly degrade spiral performance. Some designers use a zigzag spiral as a slow wave structure to avoid added material weight. The effect of this technique may be limited in real-world applications due to self-resonance of such a slow wave structure.
Cavity Housing
A spiral antenna without a cavity housing will radiate in a bi-directional pattern on both sides of the spiral plane. A bi-directional pattern antenna is more sensitive to installation effects such as scattering from the mounting surface. Because of this, uni-directional patterns are more desirable.
One technique to convert a bi-directional to a uni-directional pattern is to use a cavity. Basically, the spiral becomes a probe that excites the cavity. This is similar to how a probe excites a circular waveguide. Typically, the cavity diameter is slightly larger than the spiral diameter. The cavity depth should be at least one quarter wavelength at the lowest frequency if no cavity absorber is used. Due to a constructive reflection from the cavity bottom wall with a quarterwave spacing, this unloaded cavity-backed spiral should nominally yield an additional 3 dB more gain than spirals backed by an absorber-loaded cavity. This gain benefit is at the expense of losing frequency independence from the quarterwave spacing. In other words, the unloaded cavity-backed spiral frequency performance is reduced to approximately a 2:1 bandwidth.
In some occasions, designers may need to trade off gain and bandwidth to meet system requirements. Designing absorber loading inside a cavity is considered an engineering art that requires many years of spiral design experience, computer simulations and laboratory testing. This would require a separate article devoted to that topic alone and is not discussed here.
Amplitude and Phase Tracking
An array of multiple spirals with proper translational displacements can be used as a radio frequency (RF) phase interferometer for ESM applications. These spirals typically have phase tracking performance that assures certain system AoA performance. Phase tracking is normally defined as a statistical measure of uniformity of phase over a specified frequency, polarization, azimuth and elevation, compared to a golden standard spiral antenna. A typical measure of statistical uniformity is the root mean square (RMS) of the phase difference between the spiral antenna under test and a golden standard spiral. This is an important performance parameter because the system AoA error is directly correlated with such phase tracking errors, some of which may not be corrected as part of the antenna calibration plan, due to certain system architectures. In other words, high-performance spirals are expected to have superior phase and/or amplitude tracking performance. Typical phase tracking performance is on the order of 6º RMS and amplitude tracking values are on the order of 0.7 dB RMS. To meet such stringent tracking performance, the spiral design needs to be fully optimized, including the spiral structure, balun, cavity, terminations and absorber loading. Any higher-order spiral modes, if excited, could cause serious pattern asymmetry or axial ratio degradation, which could lead to poor tracking performance.
Spiral Limitations
Although spiral antennas have many properties suitable for EW/ESM applications, they have some inherent limitations. One well-known limitation is lower aperture efficiency, hence lower gain for the given aperture size. This is due to the inherent frequency-independent nature of a spiral antenna. As frequency increases, the aperture electrical size proportionally increases. But, because the spiral is a frequency-independent antenna, its gain is unchanged as frequency increases. In other words, unlike a resonant antenna, some of the spiral aperture is wasted when operated in the higher frequency portion of its band.
One limitation of a spiral antenna is its susceptibility to high RF power handling. A good spiral design may be able to handle a few watts average RF power in the Ku frequency band, but is limited due to thermal issues of the currents on the small line width spiral arms. In addition, because of the spiral line-to-line spacing along the spiral arms, high field strength arcing can occur if the electric field strength exceeds the air breakdown limit. One mitigation design technique is to use an Archimedean spiral of constant line width near the spiral center. However, this becomes a tradeoff between the line-to-line spacing and high field strength handling. The line-to-line spacing is related to the self-complementary property of the spiral, especially in the higher frequency band. As a result, designers may need to compromise performance at higher frequency with high field strength handling.
Another limitation is off-axis elevation performance. The two-armed spiral, if designed properly, should have good pattern symmetry at 0° elevation. For higher or lower elevations in a conical cut, symmetry starts to deviate due to depolarization effects. This is caused by electric currents on the spiral arms and magnetic currents on the cavity aperture interacting destructively off the principal plane. Design options to mitigate depolarization include: a) Use of as much complementary design as possible to increase rotational symmetry; b) Optimized cavity diameter size to avoid higher order mode excitations; c) Use of four-armed spirals to effectively double the rotational symmetry.
Conclusion
The basic spiral antenna design techniques have been reviewed. It has been shown that by use of some understandable engineering principles without complicated mathematics, a spiral antenna can be designed to have reasonable performance. However, spiral antenna design is becoming more challenging due to even smaller size and lighter weight requirements in today’s more advanced EW systems. Although spiral antennas have existed over four decades, their design maturity for new requirement challenges, in the authors’ opinion, is still evolving.
References
- B.H. Burdine, The Spiral Antenna, Massachusetts Institute of Technology, Research Laboratory Technical Report, April 1955.
- J.D. Dyson, “The Equiangular Spiral Antenna,”IRE Transactions on Antennas and Propagation, Vol. 7, No. 2, April 1959, pp. 181-187.
- J.A. Kaiser, “The Archimedean Two-Wire Spiral Antenna,” IRE Transactions on Antennas and Propagation, Vol. 8, No. 3, May 1960, pp. 312-323.
- T. Milligan, Modern Antenna Design, McGraw Hill, New York, NY, 1985, pp. 372.
Tom Lam is a qualified architect in Lockheed Martin Mission Systems and Sensors (MS2). He holds a MSEE from Polytech/NYU. He is a recipient of the 2012 Asian American Engineer of the Year (AAEOY) award. He has over 25 years of experience in antenna/radome designs and co-site interference modeling and mitigations.
Rich Bidwell has been a lead antenna engineer at Lockheed Martin MS2 for over a decade, responsible for E-2C/D and MH60R ESM systems and A10 RF systems. He is the lead engineer for the MS2’s Compact Range facility.
Scott Blee is an engineering aide senior specialist in Lockheed Martin MS2. He holds an AAS Electrical Engineering Technology from Broome Community College, Binghamton, NY. He has four years of experience as a Naval Service Aviation Electronics Technician (Weapons, Radar and Communications Systems). He has over nine years experience in RF circuit evaluation and antenna/radome design and test.
