A K-Band bandpass filter, using a single ridge waveguide and capacity-loading posts, is presented in this article. It is based on transmission line and ridged waveguide theories. In contrast to the traditional evanescent-mode ridged waveguide filters, the width of both ridge and capacitor-loading post of the proposed new type of the ridged waveguide bandpass filter are the same. A filter is designed, simulated and fabricated at 22.3 GHz, demonstrating a fractional bandwidth of 42.2 percent, from 17.6 to 27 GHz, a VSWR less than 1.5 and an out-of-band rejection of −60 dB at 15 and 30 GHz, respectively. Based upon these good performances, the proposed ridged waveguide filter can be used in microwave and millimeter wave communication systems.
Waveguide bandpass filters are playing an increasingly important role in modern communication systems and other microwave fields. With the rapid development of modern microwave and millimeter wave communication systems, the requirement for filters with high performance, wide bandwidth and small size is growing.
To make the waveguide filter more compact, a traditional resonator is modified in order to obtain multiple resonant frequencies. Hence, one resonator can be treated as the equivalent of multiple resonators. The dual-mode filter is one of the most widely used in multiple-mode filters that have been developed.1-3 However, the limitation for such a filter is that the width of a dual-mode filter is greater than that of traditional rectangular waveguide filters.
Evanescent-mode filters have been proposed by Graven to reduce the width of the waveguide filter and the technology had been applied for years.3-6 Besides, the evanescent- mode filters perform well in out-of-band rejection. And they have small size and light weight, making such filters more widely used in microwave and millimeter wave systems.
Evanescent-mode ridged waveguide bandpass filters have been developed7-9 where various configurations of ridge are used and wide spurious-free out-of-band responses are achieved. However, the disadvantage of this technology is that the different cross sections of the cavity make the fabrication difficult for building a wideband filter.
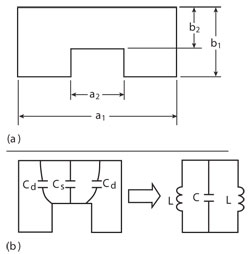
Figure 1 Single ridged waveguide (a) cross section, (b) equivalent circuit.
Cohn has reported the ridge waveguide and analyzed its properties.10 Because of its high power capacity, low insertion loss and good frequency selectiveness, the ridged waveguide filter has attracted attention, followed by many reports on the subject, to reduce the size of the filters.11-12 Compared to rectangular waveguides, ridged waveguides have the advantages of wide fundamental-mode operating bandwidth, low cutoff frequency and low wave impedance.10-11 Fundamental-mode operating bandwidth of four to one or more is easily obtainable with ridged waveguides. The low cutoff frequency yields a small cross section and hence, a compact size ridged waveguide component can be achieved. The low wave impedance allows an easy transition to planar transmission lines such as strip lines or microstrip lines. Therefore, ridged waveguide bandpass filters are the ideal components for these applications.
In this article, a new type of 10-order, wideband bandpass filter, employing ridged waveguide and capacitor-loading is proposed. It is noticed that the widths of the ridge and posts are identical, making the manufacturing process convenient. The design specifications for the filter are a 22.3 GHz center frequency, demonstrating a fractional bandwidth of 42.2 percent, from 17.6 to 27 GHz, with a VSWR less than 1.5, an out-of-band rejection at 15 and 30 GHz less than –60 dB, respectively. The bandpass filter was fabricated and measured. Both the simulated and measured results are presented.
Theory and Analysis
For the cross section of the single ridged waveguide shown in Figure 1, the width and height of the single ridged waveguide are a1 and b1. The width of the ridge is a2 and b2 is the distance from the top of the ridge to the top of the waveguide. The equivalent circuit is also shown, where Csis the electrostatic capacitance originating between the ridge and ground, while Cddenotes the capacitance formed from the discontinuity of the ridge. L is the equivalent inductance of the waveguide from the two sides of the ridge.
The capacitance Cs is given by:

where ε1is the dielectric constant of the medium. The capacitance Cddepends on the b2/b1 ratio. Using a conformal transformation, Cdcan be expressed as follows13
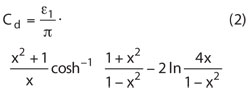
where x represents b2/b1. Hence, the total capacitance per unit length can be expressed as
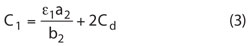
Theequivalent inductance per unit length is expressed as
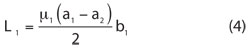
where μ1is the permeability of the medium. The cutoff frequency of the ridged waveguide f'ccan be expressed using Equations 3 and 4 as follows:

The cut off wavelength of the ridged waveguide can be expressed as
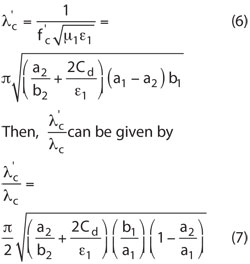
where λcis the cutoff wavelength of the dominant mode of the rectangular waveguide. Here a = 4.5 mm, then
Substituting b = b1 = 2.9 mm yields,11

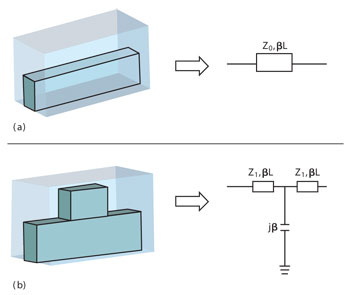
Figure 2 Ridge waveguide and equivalent circuit, (a) single ridge, (b) capacity loaded ridge.
Here, the λ'c10is the fundamental-mode cutoff wavelength of the ridged waveguide. Thus, λ'c10= 3.8 x 34.5 = 17.1 mm, far longer than the cutoff wavelength of the traditional waveguide.
It is noted that the conventional single ridged waveguide structure shown in Figure 2 can be regarded as a specific case of transmission line. From transmission line theory, the capacity-loaded ridged waveguide equivalent circuit is also shown. The conventional ridged waveguide transmission line has the impedance Z0and electrical length βL, while its corresponding capacity-loaded transmission line is made up of two symmetric sections of transmission lines with the impedance Z1, electrical length β1l and capacitance represented by the susceptance jβ. Discussed from the point of transmission line, the network functions are:
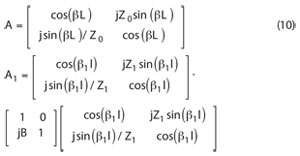

where matrix A means the network function of the traditional ridged waveguide transmission line and matrix A1 represents the network function of the equivalent compounded capacity-loaded transmission line. If the two matrix have the relation that A = A1, from Equations 10 and 11, one obtains,

when BZ1is large enough, 2β1l can be considerably smaller than π/2, that is, the total length of the compound transmission line is much shorter than the length of its equivalent conventional transmission line.
Therefore, the length of the cavity can be reduced by capacitor-loading. On the other hand, the ridged waveguide serves as a way to obtain wide bandwidth, since its dominant mode frequency is lower compared to a conventional waveguide and the frequency of first higher-order mode (TE20) is higher than that of a conventional waveguide. Hence, by using capacitor-loading in ridged waveguide, good performance with small size and wide bandwidth can be realized.
Design, Simulation and Measured Results
The design specification is to build a filter whose center frequency is 22.3 GHz, demonstrating a fractional bandwidth of 42.2 percent, from 17.6 to 27 GHz, with a VSWR less than 1.5 and out band rejection at 15 and 30 GHz less than –60 dB, respectively.
A mode-matching technique is used to build exact numerical models of the rectangular-to-ridged waveguide junction as filter key elements. The full-wave-matrix of a rectangular waveguide bifurcation was calculated in accordance with the technique described by Vasilyeva et al.14 The generalized scattering matrix of the discontinuity is obtained using the mode-matching method.15 The analysis of combined filter components, as well as the analysis of a filter as a whole, was performed by the generalized-matrix technique. The improved procedure of the prototype filter synthesis was used to obtain an initial filter configuration needed to feed the optimization procedure.16 The latter was based on the multi-parametric gradient approach and worked in some stages with different goal functions. At the first stage, a special emphasis was put on the filter response to satisfy the specified skirt selectivity and width of the passband. At other stages, the required level of passband return loss was reached.

Figure 3 Schematic of a compact capacitor loaded ridged waveguide filter.

Figure 4 Photographs of the filter (a) inner configuration, (b) with 2.92 mm connectors.
The configuration of the 10 order capacity-loaded compact ridged waveguide filter is shown in Figure 3. It is made up of ridges with ten posts symmetrically placed in cavities. It is noticed that the width w1 of the ridge and posts is identical, making it convenient in the manufacturing process. The frequency of the passband can be adjusted by tuning the height of post hi (i = 1, 2…5). The coupling is determined by the distance of adjacent length Li (i = 1, 2…5), which can be tuned easily. Besides, two removable 2.92 mm-type coaxial connectors are used to connect with the outside. By changing the length (L0) and height of post (h0), the coupling between the cavity and the outside can be adjusted.
To meet the design requirements, a wideband waveguide filter has been designed using CST Microwave Studio. Its dimensions are as follows: L0 = 1.08 mm, L1 = 1.31 mm, L2 = 1.80 mm, L3 = 2.18 mm, L4 = 2.08 mm, L5 = 2.14 mm, L6 = 1.6 mm, lp0 = 0.92 mm, lp1 = 1.15 mm, lp = 1.5 mm, h0 = 2.9 mm, h1 = 1.48 mm, h2 = 1.45 mm, h3 = 1.27 mm, h4 = 1.34 mm, h5 = 1.30 mm, h6 = 1.73 mm, a = 4.5 mm, w = 1.5 mm.
Depending on the discussions above, a new type of ridged waveguide bandpass filter made of aluminum has been manufactured, according to the dimensions obtained from the simulation data. Figure 4 shows photographs of the fabricated filter. This type of filter is compact, with outside dimensions of 58 × 13.36 × 9.8 mm.
The broadside of the compact ridged waveguide filter is only 4.5 mm, a decrease of 57.9 percent, compared to the traditional waveguide whose broadside is 10.688 mm, allowing its more widely application in the design of microwave and communication systems.
In order to compensate for the fabricating errors, tuning screws are added in the cover plate of the filter and side of the cavity to tune the frequency and coupling error in the process of manufacturing. Also, in order to reduce the insertion loss, the filter is made of aluminum, with its inner surface plated with silver. The filter cavity and its cover were soldered.
The filter was measured at room temperature with an Agilent 8722ES vector network analyzer over the frequency range from 50 MHz to 40 GHz. A 50 Ω matching load was used in the measurement. Two 2.92 mm-type connectors were used for testing. The simulated and measured results of the proposed filter are shown in Figure 5. The results show that the proposed filter has a wide bandwidth from 17.6 to 27 GHz with a fractional bandwidth (FBW) of 42.2 percent at a center frequency of 22.3 GHz. The minimum insertion loss measured is found to be less than 0.6 dB, except at the lower and upper edges of the passband, where the loss is less than 0.8 dB. The measured return loss is better than 15 dB over the whole passband.
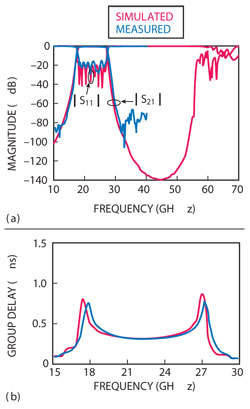
Figure 5 Simulated and measured performance of the filter (a) S-parameters, (b) group delay.
Meanwhile, the implemented filter exhibits a flat group delay response, which is below 0.6 ns. The group delay variation is less than 0.3 ns at the lower and upper passband edges. At 3 GHz away from the passband, the out-of-band rejections are less than –61 and –63 dB, respectively. The measured results and simulations agree well in both magnitude and trend. Hence, these results verify this design method.
Conclusion
In this article, a new type of ridged bandpass filter with capacitor-loading has been designed, fabricated and measured. When compared with typical evanescent-mode ridge waveguide filters, the proposed new type of ridged waveguide bandpass filter is easier to fabricate, with the same width of the ridge and capacitor-loading post. The resonant frequencies can be easily adjusted by tuning the height of the posts. The coupling is determined by the distance of adjacent length, making it convenient in the process of designing and manufacturing. It provides a convenient method of designing a compact wideband ridged waveguide filter. Both the simulated and measured results are presented and discussed. The superior features of designing this kind of filter indicates that it has the potential to be utilized in microwave and millimeter wave communication systems.
Acknowledgment
This project was supported by the Science and Technology Bureau of Sichuan Province, China (No. M110104012008HH0013/2008FX0023/2009GZ0006) and Chengdu Science and Technology Bureau of Sichuan Province, China (No. M1701040110YTYB022G).
References
1. J.F. Liang, X.P. Liang, K.A. Zaki and A.E. Atia, “Dual-Mode Dielectric or Air-Filled Rectangular Waveguide Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 42, No. 7, July 1994, pp. 1330-1336.
2. S. Amari and M. Bekheit, “A New Class of Dual-Mode Dual-Band Waveguide Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 56, No. 8, August 2008, pp. 1938-1944.
3. S. Bastioli, C. Tomassoni and R. Sorrentino, “A New Class of Waveguide Dual-Mode Filters Using TM and Nonresonating Modes,” IEEE Transactions on Microwave Theory and Techniques,Vol. 58, No. 12, December 2010, pp. 3909-3917.
4. G. Craven, “Waveguide Bandpass Filters Using Evanescent Modes,” Electronics Letters, Vol. 2, No. 7, July 1966, pp. 251-252.
5. Q. Zhang and T. Itoh, “Computer-aided Design of Evanescent-mode Waveguide Filter with Nontouching E-plane Fins,” IEEE Transactions on Microwave Theory and Techniques, Vol. 36, No. 2,February 1988, pp. 404-412.
6. L.S. Wu, X.L. Zhou and W.Y. Yin, “Evanescent-Mode Bandpass Filters Using Folded and Ridge Substrate Integrated Waveguides (SIW),” IEEE Microwave and Wireless Components, Vol. 19, No. 3, March 2009, pp. 161-163.
7. A. Kirilenko, L. Rud, V. Tkachenko and D. Kulik, “Evanescent-mode Ridged Waveguide Bandpass Filters With Improved Performance,” IEEE Transactions on Microwave Theory and Techniques, Vol. 50, No. 5, May 2002, pp. 1324-1327.
8. T. Shen and K.A. Zaki, “Length Reduction of Evanescent-Mode Ridge Waveguide Bandpass Filters,” Progress In Electromagnetics Research, Vol. 40, 2003, pp. 71-90.
9. C. Rauscher and S.W. Kirchoefer, “Miniature Ridge-waveguide Filter Module Employing Moldable Dielectric Material,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 3, March 2006, pp. 1190-1196.
10. S.B. Cohn, “Properties of Ridge Waveguide,” Proceedings of the IRE, Vol. 35, No. 8, August 1947, pp. 783-788.
11. S. Hopfer, “The Design of Ridged Waveguides,” IRE Transactions on Microwave Theory and Techniques, Vol. 5, No. 5, October 1955, pp. 20-29.
12. M.M. Fahmi, J.A. Ruiz-Cruz, R.R. Mansour and K. . Zaki, “Compact Ridge Waveguide Filters With Arbitrarily Placed Transmission Zeros Using Nonresonating Nodes,” IEEE Transactions on Microwave Theory and Techniques, Vol. 57, No. 12, December 2009, pp. 3354-3361.
13. R.E. Collin, Foundations for Microwave Engineering, 2nd Ed., McGraw-Hill, New York, N.Y., 1992.
14. T. Vasilyeva, A. Kirilenko, L. Rud and V. Tkachenko, “Calculation of Full-wave S-matrices of Monoaxially Uniform (2D) Elements In Rectangular Waveguides,” Proceedings of the 7th international Conference on Mathematical Methods in Electromagnetic Theory, Vol. 1, 1998, pp. 399-401.
15. C. Wang and K.A. Zaki, “Full-wave Modeling of Generalized Double Ridge Waveguide T-junctions,” IEEE Transactions on Microwave Theory and Techniques, Vol. 44, No. 12, December 1996, pp. 2536-2542.
16. A. Kirilenko, L. Rud, V. Tkachenko and D. Kulik, “Design of Bandpass and Lowpass Evanescent-mode Filters on Ridged Waveguides,” Proceedings of the 29th European Microwave Conference, Vol. 3, 1999, pp. 239-242.
