Phase noise is a property of an oscillator that can extend in magnitude from the carrier of several volts down to a mere nano-volt far from the carrier. In many cases the lowest noise OCXOs, SAWs and other specialty oscillators have carrier to noise ratios in excess of -180 dBc√Hz. The noise level of these oscillators often extends below that of even the mixers and low noise amplifiers at baseband. Cross correlation is a method used in phase noise analysis to extend the range of any single channel measurement by introducing a second channel and utilizing signal processing to locate the noise that is common to the DUT, yet uncommon to each individual channel. With this method, a typical noise floor improvement of 20 dB is very realistic, allowing for high accuracy measurements of extremely low noise oscillators. This article presents the mathematics with an example of how cross correlation can accurately identify signals or noise that is below the level of the measurement instrument.
Most phase noise measurement systems use what is called carrier cancellation. Phase noise is not measured directly, but down-converted to baseband. In an absolute phase noise measurement, where the absolute noise level of an oscillator is being measured, two oscillators are phase locked to one another. Once the two signals are locked with a mixer, the phase noise of both channels is down-converted directly to baseband without the carrier which is at DC and cancelled.
In a residual or additive phase noise measurement, whereby the additive noise of a component such as an amplifier is to be measured, the oscillator is split into two parts. One path drives the LO port of the mixer while the other path goes through the DUT prior to going into the RF port of the mixer. Within the noise level and isolation of the mixer, the carrier and its noise are canceled, being common between the two paths, while the noise of the DUT is measured directly at an offset and its carrier frequency centered at DC.
In both cases, low noise, low frequency techniques are then applied to amplify and sample this signal. However, in both cases, noise levels of system components may limit the measurement dynamic range or noise floor. In absolute measurements, the reference oscillator typically is the limitation. In additive measurements, even a very good mixer can often contribute as much noise as a low noise DUT.
Cross correlation has been used by NIST for metrology level phase noise measurements for quite some time (see the references for more information or go to www.nist.gov). Throughout this article noise is normalized to per root Hz from equation 1 where B = 1 Hz. Many times the reader may see per Hz, but usually that is an artifact of not having the proper symbol available. Since the square root of 1 is 1, many just ignore this difference even if it is not correct.
NOISE SOURCES
The need for cross correlation is best illustrated via an example. Assume a very high quality oscillator having a phase noise floor of -180 dBc/√Hz with +10 dBm output power. The white noise power of the oscillator is equal to 10 dBm (-180 dBc/√Hz) or -170 dBm/√Hz. A 50 Ω resistor exhibits about 0.9 nV/√Hz of noise or -174 dBm/√Hz in terms of power. A noise power of -170 dBm/√Hz is only 1.44 nVrms/√Hz. The best low noise amplifiers are near 1 nVrms/√Hz self noise, limiting both the accuracy and sensitivity of the measurement. This is assuming an ideal phase detector with no loss or noise itself.

To evaluate whether a 'real' mixer could deal with this level of noise, we continue with the example. A 13 dBm high quality mixer phase detector may be driven around 5 dBm at the RF port. At this level, the mixer is slightly in compression with a conversion loss of likely about 7 dB. The output phase conversion may be Kd=0.4 V/rad or about 0.282 Vrms/rad. With a 50 Ω resistor exhibiting about 0.9 nVrms/√Hz, this leaves a dynamic range of -170 dBc/Hz (about 10 dB below that of the oscillator). A higher power mixer can increase this dynamic range, but shot noise and other effects can become more dominant (such as the combined impedance of the mixer and the termination at the IF port). Table 1 shows the voltage noise of several different resistance values, demonstrating that higher equivalent resistances can significantly degrade the signal to noise ratio. An equivalent port impedance of 100 Ω can decrease the signal to noise ratio by 3 dB.

In an absolute phase noise measurement, the reference oscillator will likely contribute significantly more noise than the mixer, especially at close to the carrier. In an additive measurement such as a low noise, silicon BJT-based RF amplifier, the RF amplifier may have noise that is on par with the silicon diodes used in a good phase detector. In both examples, it is clear that low noise devices require additional techniques to accurately measure them down to very low levels.
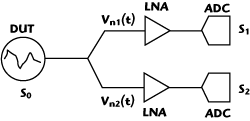
Figure 1 Block diagram of noise measurement system where one signal with noise is measured simultaneously by two channels with their own independent and uncorreclated noise sources.
CROSS CORRELATION
A diagram of a two-channel cross-correlation system to measure noise or very small signals is shown in Figure 1. Signal S0 is common while each individual channel has its own independent, and higher, noise. The resultant time domain sampled signal is in the form of S1 and S2. The desired signal to be measured is S0 and has a small-signal component and broadband noise:

The actual measured signal from channels 1 and 2 are defined as

MATHEMATICAL DEFINITIONS
Cross correlation can be computed via convolution or as a Fourier transform. In the case of spectral analysis, it is easiest to deal with the Fourier transform version. Cross correlation in the time domain is defined by convolution as

The star is representative of the mathematical function of convolution. The asterisk denotes the complex conjugates of signal S1. Rewritten in terms of a Fourier transform, the Fourier transform of the cross correlation is the dot product of the complex conjugate of one Fourier transform to the other Fourier transform.

It is shown here that cross correlation makes use of the phase information relative to the two channels. Figure 2 is a phasor diagram of the magnitude and phase of the Fourier transform for a given frequency component. The red signal vector is the buried signal representative of S0 while the gray vectors are the random contributions of the whole system noise levels, S1 or S2. The gray vectors are unique and uncorrelated for each channel for each measurement while the red vector is common. Figure 2 illustrates how a buried signal phasor relates to the overall random noise vectors. Two channels will measure the buried signal vector identically with uncorrelated and larger noise in sum with it. Vector averaging the dot product of the two channels (one as a complex conjugate) will reduce the uncorrelated noise proportional to the number of correlations. Vector averaging a number of cross correlations is known as 'cross correlating' with a number of correlations.
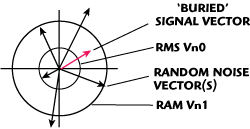
Figure 2 Phasor diagram of the vector Fourier component of any given frequency.
The dot product of one signal with the complex conjugate of another for two identical signals results in just the magnitude squared of either signal and is real, having a phase of zero. The dot product of the complex conjugate of one uncorrelated signal to another will be random in both magnitude and phase.
VECTOR AVERAGING THE CROSS CORRELATION
In a single channel magnitude only system, each frequency bin magnitude is summed and then divided by the number of measurements to achieve averaging. In a cross-correlation system, both the magnitude and phase, or real and imaginary parts of the dot product from the cross correlation are vector summed. The dot product of the random noise vectors will eventually achieve a vector sum of zero assuming they are truly random and uncorrelated. The dot product of the small common signal will be in phase and real and eventually be the only signal left.
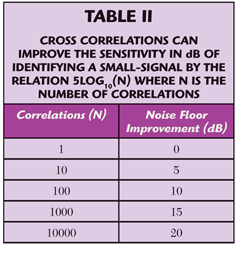
Vector averaging yields a maximum improvement relative to the number of averages (N) in dB as 5log10(N). In other words, it takes an order of magnitude increase in measurements for every 5 dB improvement. Table 2 lists the improvement for a number of correlations.
EXAMPLE
To illustrate how cross correlation works, a mathematical equivalent of Figure 1 was defined in numerical computing software using the signals S0, S1 and S2. S0 represents a small-signal above a broadband low noise level equivalent to just over a 50 Ω noise floor. S1 and S2 contain noise components vn1 and vn2, respectively, with noise levels that are above that of the small-signal of S0. The example demonstrates that a single channel system could never measure S0, given the noise levels of the receiver with resultant signal S1.

Figure 3 Hann window filter to be applied to a 1024 point time domain sample.
WINDOWING
Window filtering is an important step in noise analysis. Discontinuities that occur during the start and stop of the finite sampling of a signal can cause spectral-leakage from one frequency to another, once the Fourier transform is applied. In low dynamic range systems, such as a 6- or 8-bit oscilloscope, this may not have much of an effect. However, with higher dynamic range systems (>60 dB), this can cause significant problems. To overcome this, the input time domain signal is windowed with an additional function to reduce this effect. For this example, we use the Hann window shown in Figure 3, one of the more common windows used with noise analysis. The Hann window is defined as


Figure 4 Time domain signal of S0 before and after application of a Hann filter.

Figure 5 Time domain of 'system' S1 with superimposed time domain of desired signal.
where N is the number of time domain samples. In this example we use 1024 points. Windowing of the ideal signal S0 is shown in Figure 4. In a real (noisy) measurement system, with noise components vn1 and vn2 being greater than signal S0, the actual measurement is going to look more like Figure 5. For comparison, Figure 5 shows the ideal S0 superimposed with the measured system signal S1.

Figure 6 The three traces represent signal S0, S1, and the cross-correlation of S0 and S1 with 1 correlation.

Figure 7 The three traces represent signal S0, S1, and the cross-correlation of S0 and S1 with 100 correlations.

Figure 8 The three traces represent signal S0, S1, and the cross-correlation of S0 and S1 with 10,000 correlations.
At this point, the cross-correlation algorithm is applied to signals S1 and S2 with vector averaging (cross correlations) at 1, 100 and 10,000 for a maximum improvement of 0, 10 and 20 dB, respectively. Figures 6, 7 and 8 demonstrate the effectiveness of cross correlation for 1, 100 and 10k correlations, respectively. Each plot contains three curves. The blue curve is the ideal signal S0, having the number of correlations equal to the number of averages. The red curve is the signal S1 of the individual channel, having the number of correlations equal to the number of averages. The yellow curve is the resultant cross correlation after vector averaging the number of 'correlations'. The results are tabulated in Table 3, respective of the number of correlations.
CONCLUSION
Cross-correlation analysis trades measurement setup complexity and time for increased sensitivity. In situations such as measuring phase noise where hardware can limit the measurement sensitivity compared to the device under test, cross correlation may be applied to improve the sensitivity to acceptable levels. In cases where the measurement floor is still below the device under test, but very close, cross correlation will improve the overall accuracy of the measurement. For cross correlation to be most effective, each channel must be isolated as much as possible to reduce or eliminate common mode noise. Additionally, the lower the noise measurement capability of each individual channel, the fewer correlations will be required and the faster a measurement can occur. As shown in the example plots of Figures 6-8, cross correlation has the ability to pick up noise and small signals that are otherwise invisible to traditional measurement systems.

References
- W.F. Walls, "Cross-correlation Phase Noise Measurements," 1992 Frequency Control Symposium.
- E.N. Ivanov and F.L. Walls, "Interpreting Anomalously Low Voltage Noise in Two-channel Measurement Systems," IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 49, No. 1, January 2002.
- A. Hati, D.A. Howe, F.L. Walls and D. Walker, "Noise Figure vs. PM Noise Measurements: A Study at Microwave Frequencies," Proceedings of the 2003 IEEE International Frequency Control Symposium.
- http://en.wikipedia.org/wiki/Cross_correlation.
- http://en.wikipedia.org/wiki/Window_function.
