Basic antenna theory shows that the scattering cross-section of an antenna is often much larger than the physical cross-section of the metal wires from which the antenna is constructed. In the case of RFID tags, a large number of tag antennas may be present in close proximity to one another when many articles are to be tagged. In such circumstances, it is shown that strong scattering effects influence the ability to read tags due to the tag antennas. Collective scattering modulation in certain types of tags (EPCglobal class 0) is also demonstrated, which may lead to tag confusion and failures of the anti-collision procedure in the protocol. These phenomena influence the choice of antenna designs for certain applications and may limit the applicability of UHF RFID, even with the use of improved communications protocols.


The use of radio frequency communications to identify physical objects — radio frequency identification (RFID) — is an old technology that has gained increased interest of late, as reduced costs and increased capabilities have made implementations practical in the commercial supply chain.1 Low cost tracking of tagged cartons or cases can be implemented using passive tags, consisting of an etched, stamped, or printed antenna and a single integrated circuit mounted on an adhesive backing. Power is extracted from the incident RF to avoid the need to incorporate a battery, and backscattered transmission — variation in the load attached to the antenna to vary the backscattered power — is used in lieu of a local transmitter. Operation in the US ISM band at 902 to 928 MHz, or similar bands in other jurisdictions, allows resonant or near-resonant antennas of a convenient size, license-free operation and moderate range. The path loss budget for such passive tags is much less generous than is the case for a typical active radio, and represents an important constraint on the range at which the tags can be read. A typical tag IC requires around 50 to 500 microwatts to operate (that is –13 to –3 dBm). Transmitters in the US are limited to 36 dBm effective isotropic radiated power, so only approximately 40 to 50 dB of path loss is allowed before insufficient power is available to operate the tag. For example, a typical low cost WiFi (IEEE 802.11) radio has a sensitivity of around –90 dBm at 1 Mbps data rate; a passive tag is on the order of 80 dB less sensitive than a conventional radio. The range is a few meters in US operation, and tolerance to additional propagation impairment is very limited.

Today, RFID tags are generally employed to uniquely identify cases or cartons of items, each case typically tens of centimeters to over a meter on a side. Thus, even when such cases are stacked on a pallet or in a cage for transport, the density of tags is very low, and interactions between tags can be neglected (though interactions with the contents of the boxes strongly influences the received power and the read range of the tags2). In the future, however, it is anticipated that the cost of tags and readers will fall, and the infrastructure for handling information will improve, so that it will become economically advantageous to use RFID tags to identify individual consumer items. In such applications, one might expect to encounter dense regular arrays of tags, with spacing comparable to the size of the antenna. The purpose of this article is to demonstrate that in such cases, the interactions of the tags with the incident field can be large and must be accounted for. Empirical observations of tag interactions have been reported before,3 but the details of the interactions between antennas were not examined.

As background for the discussion, it is well to recall some results from basic antenna theory. An incident field encountering an antenna induces currents on the antenna, and those currents in turn radiate new fields, the net result being that some of the incident power is scattered. A convenient means of characterizing the scattering is to define a scattering cross-section: an equivalent collecting area which, when multiplied by the energy density of the impinging radiation, gives the total scattered power. For the simple case where the antenna is conjugate-matched, half of the power, Pld = P x ARX, is dissipated in the load resistor and half the power, Psc = Pld, is dissipated in the radiation resistance — scattered — so the cross-section for scattering is equal to the effective aperture ARX of the antenna (see Figure 1). This is the condition of maximum power delivered to the load, clearly desirable for maximizing the range of a passive RFID tag, so it is plausible that an RFID tag may scatter a power comparable to that it receives. In the more general case of a dipole or dipole-like antenna, with arbitrary load impedance, the effective aperture due to the total scattered power is given by4

where
G = antenna gain
Ra = antenna (radiation) resistance
ZL = complex load impedances
Za = antenna impedance
For a resonant antenna (Za = Ra), presented with a short-circuited load, the scattering aperture is four times larger than in the conjugate-matched condition, and the absorption cross-section is zero since no power is delivered (undesirable for a tag). On the other hand, increasing the load impedance will reduce the power scattered as roughly the square of the load, whereas the absorbed power will fall only linearly: one can decrease antenna scattering and still absorb power, at the cost of a reduction of absorbed power relative to that obtained from a conjugate match. Thus, the balance between absorption and scattering is dependent on the details of the tag IC load and antenna impedance. A few simple examples are provided in Table 1 to give a feel for the typical magnitudes involved. The 12 cm2 scattering cross-section for an open circuit load resistance is a measured value. The equivalent circuit model suggests that the scattered power ought to go to 0 in this case, but in fact a finite current flows in the shorter wire segments, as a more accurate model would demonstrate.
Antenna designs for passive UHF RFID tags encounter several special constraints, and are not usually simple resonant dipoles. The tag antenna is directly coupled to the integrated circuit, which presents a high resistance, slightly capacitive load. In order to provide good power match and maximize the voltage gain, most tag antennas use a short inductive stub or a folded-dipole-like configuration to resonate out the IC capacitance and match the high resistance IC. Minimizing the physical size of the antenna is a matter of considerable importance for many commercial applications. To reduce size, the antennas are often bent, wiggled, or meandered. Tip loading or bow-tie-like structures are also used to reduce the linear extent of the tag antenna and improve bandwidth. Antennas may also be bowed or curved, or multiple independent antennas employed, to provide polarization diversity. Examples of representative tag-antenna designs are shown in Figure 2. Since the absorption cross-section can never exceed the scattering cross-section, and tags must absorb power in order for the IC to turn on and respond to interrogation, tags designed for long range can be expected to have large scattering cross-sections and thus interact strongly with one another when placed in close proximity. In the remainder of this work, the results of a number of experiments are described, demonstrating the importance of tag-antenna interactions on the ability to read closely spaced passive UHF tags.

Experimental Results
Radar Cross-section Measurements
As noted above, the ability of a tag to scatter incident radiation can vary considerably depending on the geometry of the antenna and the load impedance, and tag-antenna geometries are complex and vary widely from one tag to another. Thus, it is helpful to have some measurement of the scattering properties of various tags as a guide for interpretation of experiments involving multiple scattering. Measurements of the radar cross-section (RCS) were therefore performed for a number of tags. The radar cross-section of an object is the equivalent cross-sectional area that will collect enough energy from the incident beam, re-radiated it isotropically, to match the measured backscattered signal from the object. As long as scattering is fairly isotropic, this is a reasonable surrogate for the scattering cross-section of the tag (the numerical values differ by the gain of the tag antenna, approximately 1.5 to 1.6). The setup used is depicted in Figure 3.
The measurements were performed in an anechoic chamber, using a very simple and substantially RF-inactive movable rope and plastic holder to suspend and move the tags. An HP8753 network analyzer was used to extract the reflected signal from a calibrated horizontally polarized antenna. The vector reflection coefficient of the tag was estimated by subtracting the reflection measured when the tag is not present in the chamber. Reflections were measured at various distances from the antenna and fit to the radar equation5

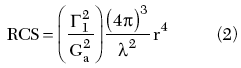
by adjusting the value of G1 to obtain an estimate of the radar cross-section.
Here
?1 = measured reflection coefficient at the antenna due to the sample
Ga = gain of the test antenna
r = sample-antenna distance
? = wavelength
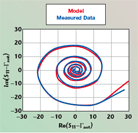
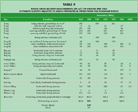
An example of the measured and modeled data is shown in Figure 4. The results are summarized in Table 2. The scattering cross-sections vary from as little as 3 cm2 to as large as 465 cm2. (Some variation is observed in measurements of nominally identical tags. There are two likely main sources of variation: the orientation of the tags is not accurately maintained by the rope suspension, and can vary by approximately 20°, and different tags of the same model often show significant variations in range, possibly reflecting varying load impedances.) This variation somewhat exaggerates the variation expected in a multiple-tag effect. Since multiple-tag scattering depends on the sum of scattered potentials and thus on the induced current rather than scattered power of each tag, it is the square root of the RCS that will determine the importance of tag interactions. This quantity still varies quite substantially, from approximately 1.7 to 22 cm, suggesting that different tags will have differing effects when present in a dense array.

Tag Read Range
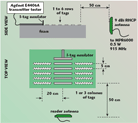
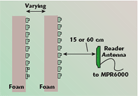
The strongest scattering effects are to be expected from tags with the largest radar cross-sections. Alien I-tags display some of the largest values of RCS in the ISM band (902 to 928 MHz), so the focus is on them first. The read range of a dense planar array of such tags was examined, first with the direction of propagation in the plane of the array (see Figure 5). The planar arrays are constructed using rows of tags, affixed to thin cardboard backing, placed onto a non-conductive foam support at spacings of 20 cm lengthwise and 5 cm perpendicular to the tag axis. The default array was configured as three columns of nine tags each. A WJ Communications MPR6000 reader, with 0.5 W transmit power, was connected to a horizontally polarized 9 dBi antenna. A total of four groups of 10 inventories were performed in each condition, with a tag reported as having been read if its electronic product code (EPC) was observed in any inventory operation. Note that it is indispensable to employ the binary tree collision resolution (‘PING’) capability available in EPCglobal class 1 tags in this environment; a ‘global scroll’ inventory will read only 2 to 4 tags, versus the 24 to 30 tags that are obtained in a single anti-collision inventory. The frequency range was limited to 923 to 925 MHz to avoid uncontrolled excursions in results due to frequency hopping.

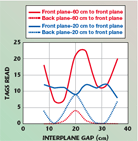
Some of the results are shown. Figure 6 shows the ability to read tags in a fully populated 3 by 9 array. The antenna was displaced laterally to view the left, center and right columns, as shown schematically in the figure. The antenna distance from the nearest tag was set at 30 or 60 cm. Since the array size is approximately 45 cm, the most distant tag was at most 1 meter from the antenna, easily within the 2.5 to 3.5 meter read range for an isolated I-tag. Thus, if scattering was negligible, all tags should have been readable. However, as shown, only the tags nearest the antenna were accessible. It is also notable that the center column is read very poorly, with at most 5 out of 9 tags, whereas the left and right columns both provide read-outs to the seventh tag. Increasing the tag-antenna distance from 30 to 60 cm results in a slight improvement in the number of tags read. The ability to read the most distant row when the effects of other tags are removed is examined in Figure 7. When only three rows are populated, the most distant tag in the center column is read (top). When only the most distant row is populated, all the distant tags are read (bottom), verifying that even the most distant row can be seen by the reader when the intervening tags are removed. Finally, Figure 8 shows that the effects are not confined to the line of sight: when the left column of tags is removed, the center column (heretofore mostly invisible) becomes largely read, and when both side columns are removed, the center column is read in its entirety. A second geometry of considerable practical interest is a multiplane array (as the first step towards a full three-dimensional array). A two-plane array was examined, consisting of the 3 by 9 array shown above, arranged in front of a 3 by 6 array with the same spacing (see Figure 9). The distance between the planes of tags (interplane gap) was varied and the number of tags read in the front and back planes was recorded. The resulting tags, read as a function of interplane gap, are shown in Figure 10. If only the line of sight was important, it might be expected that the two planes would interact only weakly and most or all tags in both planes would be read. However, the results show that this is not the case. The back plane of tags is nearly invisible except at an optimal spacing of approximately 20 cm, and the ability to read tags in the front plane is strongly influenced by the presence of the back plane. Furthermore, the front-plane readability at 60 cm spacing to the antenna shows pronounced periodicity of roughly 16 cm, corresponding to approximately 1/2 wavelength at the operating frequency. This result is qualitatively similar to that one might expect from a solid metal reflector: constructive interference at odd quarter-wavelength spacings increases the field at the front plane.
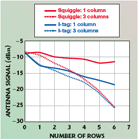
From the results of Table 2, it might be expected that the effects of scattering would be reduced using a Squiggle tag in place of an I-tag, for example, as the RCS of the Squiggle is much smaller. Figure 11 shows the results of an experimental configuration essentially identical to that used before, except that Squiggle tags are substituted for I-tags (in the same positions). The distance between the antenna and the nearest tag is 50 cm. In contradistinction to the previous results, here almost all tags are read when the antenna is centered on the array, and predominantly only the most distant tags from the antenna fail to be read.
Figure 12 shows the analogous result for multiple planes of tags. The visibility of both planes is considerably higher than was the case for I-tags, but it is also obvious that scattering effects remain of considerable importance: the visibility of both planes is again strongly and periodically dependent on the spacing between them.
Also, non-negligible scattering effects have been observed at lower tag densities. In one set of experiments, using the configuration depicted in Figure 13, Symbol X-tags (folded just below the IC for mounting convenience) were laid out on a set of wooden tables over an area of roughly 3 by 2 meters. The rows were populated with three tags each (as shown) or 10 tags each. The row-to-row spacing was approximately 30 cm; the column-to-column spacing was approximately 90 cm (three tags per row) or 20 cm (10 tags per row). The tags were illuminated by the same reader and antenna setup using a vertically polarized antenna to minimize floor reflections.
As shown in Figure 14, when only three tags per row were present, tags as far as 2.5 meters from the antenna were read. (Note that the range along the center column was less than that observed in the left and right columns, suggesting that even at this low tag density scattering of the signal limits the range.) When each column is populated with 10 tags, the range is reduced to approximately 1.5 meters.
In order to examine the role of scattering in the plane, empty cardboard boxes were used to elevate the front few rows of tags, as shown in Figure 15. The results, shown in Figure 16, provide a vivid illustration of the importance of in-plane scattering, as well as confirming that it is other tags and not any limit on read range that is making distant rows invisible. When the first four rows are elevated, the fifth row, sporadically visible before, is almost completely read at 27 dBm transmit power, and the sixth and seventh rows become partially visible. If two additional rows are elevated (see Figure 17), rows 7 and 8 become partially visible, even though the nearer (but shadowed) rows 5 and 6 are not read at all. Note that these fairly strong effects are observed despite the fact that, according to Table 2, the folded X-tags present a rather modest RCS of approximately 15 to 20 square centimeters when oriented perpendicular to the incident polarization, as is the case here.
Direct Measurements of Signal Strength
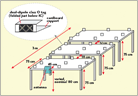
In order to demonstrate quantitatively the effects of tags on the received signal strength, a tag-like antenna was used to sample the local field strength as RFID tags were added near the receiving antenna. The configuration is shown in Figure 18. An I-tag-like dipole antenna fabricated on 0.35 mm FR4 was employed to collect the transmitted signal from the reader; an Agilent transmitter tester displayed the time-dependent signal and allowed selection of the CW portion or modulated portions as desired. An MPR6000 reader provided the illumination, with the frequency fixed at 915 MHz, driving a 9 dBi right-hand-circular-polarized patch antenna. Tag arrays were constructed between the receiving antenna and the reader antenna, using either I-tags or Squiggle tags, both mounted on cardboard, the whole assembly supported on a block of non-conductive foam. A spacing of 5 cm between rows was used. The data was taken with either one central column of tags, or three columns of tags; in the latter case, the centers of the tags in adjacent columns were spaced by 20 cm.
Figure 19 shows the signal power during the CW period of an inventory, versus the number of rows and columns, and the type of tag. As might be expected from previous results (Figures 6 and 11), I-tags have a larger effect on the received signal than Squiggle tags. The overall effect on the received signal is quite substantial, given the constrained forward link budgets for passive tags, and readily explains the difficulties previously noted in reading the rear rows of dense I-tag arrays. A single column of Squiggle tags has little effect on received power, though a dense array of three columns with more than four rows of Squiggle tags results in more than 10 dB of attenuation of the received signal.

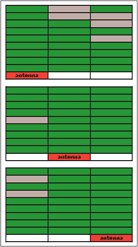
An interesting related phenomenon is the question of collective modulation of the received signal by other tags. The EPCglobal class 0 standard uses a bit-by-bit communications protocol in which tags backscatter using the continuous-wave portion of each bit symbol from the reader. One option for collision resolution uses the tag EPCs as guidance for navigation of the binary tree by the reader: each tag scatters the next bit of its EPC, and if it hears the reader echo that bit, it continues by scattering the next bit. Otherwise, it falls silent until the next attempt to traverse the tree. If all the tags in an array share many initial bits, all tags will scatter in unison during a significant portion of the tree traversal. Substantial time-dependent scattering, and thus changes in the received signal in a specific tag, can result. To demonstrate this effect, a similar experiment was performed using Symbol class 0 ‘Bag Tags.’ A dense array of ‘Bag Tags’ was mounted on a foam support, with roughly 5 cm and 12 cm spacings (some inlays varied in size by approximately 1 cm resulting in modest displacements). A reader-receiver spacing of 75 cm was used in this experiment. The reader was instructed to identify individual tags using the tag EPC (known as ID2 in the terminology used in the standard). A portion of a resulting inventory operation is shown in Figure 20. In this diagram, the 3 or 6 microsecond wide deep pulses are the reader symbols binary 0 and 1. After each such pulse, the reader signal goes HIGH for the remaining 20 or so microseconds of the symbol. During this time, the tags scatter their reply at either 2.2 or 3.3 MHz, visible as the rapid variations in signal strength. The large variation in the amplitude of the tag signal seen from one symbol to the next is not the result of a change in the number of tags responding as, in this portion of the traversal, all tags share the same EPC bits. Rather, it seems to reflect variations in the timing of the various local MHz tag oscillators, so that the various tags sometimes modulate in unison and sometimes fall out of phase. The magnitude of these collective effects is substantial. Even when the tags appear to be out of phase, the average signal strength is reduced by 6 dB below the reader CW level, which is already attenuated by approximately 17 dB below the unobstructed signal strength. When the tags scatter in unison, an 18 dB dynamic swing in received power is observed. These large changes in received power may be sufficient to interfere with the ability of the tags to correctly decode the reader symbols, with detrimental effects on the operation of the protocol. For example, if a tag that has fallen out of a traversal decodes a ‘NULL’ symbol (an extra-long LOW pulse, here around nine microseconds) followed by a ‘0,’ it assumes a new traversal has started and begins to backscatter its EPC. The reduction in signal strength resulting as other tags scatter might be mistaken for a long LOW pulse, causing a tag to re-enter the traversal in the middle and possibly block any tag from being read for that traversal.
Conclusion
These results clearly indicate that RFID tag antennas scatter incident radiation and collectively have significant effects on neighboring tags. The practical result is that dense arrays of tags will limit read range to much shorter distances than expected for an isolated tag of the same design. Scattering effects are observed for both EPCglobal class 0 and class 1 tags, suggesting that they are not artifacts of any particular protocol. The magnitude of these effects is generally correlated with the radar cross-section of an isolated tag. Protocols in which tags modulate collectively may produce significant dynamic modulation of the reader signal. This effect should take place for class 0 and class 1 tags, and may lead to artifacts in class 0 as tags mistake collective modulation of reader CW signals for reader symbols. (Note that in the EPCglobal class 1 gen II protocol, a slotted Aloha collision resolution method is used, in which it is unlikely that more than one or two tags will modulate at once.) The results suggest that optimal tag types for dense tag environments differ considerably from optimal isolated tags. For example, I-tags provide high performance as isolated tags, with relatively long read ranges, but when placed in a dense array are inferior in performance to the Squiggle tags, a distinction explained by the difference in their radar cross-sections. Tags with small RCS are preferred for dense environments, but some results show that, even in this case, scattering effects cannot be neglected. Finally, in the case where the impinging radiation is close to a plane wave, one would expect a regular array of low RCS tag antennas to produce strongly enhanced scattered fields along low index directions in the reciprocal lattice if the spacing is larger than a wavelength. In most cases, such arrays will be composed of cases with cubic or rectangular prism shape, and thus the array is cubic or orthorhombic.6 For these lattices, the reciprocal lattice vectors are in the same direction as the low index directions of the physical lattice; that is, for a three-dimensional lattice (a stack of tagged boxes) the (100), (110) and (111) directions will show strong reflections. Arrays may thus act as directive reflectors, possibly causing reader-reader interference and tag reads in unexpected locations.

References
1. D. Dobkin and T. Wandinger, “A Radio-oriented Introduction to Radio Frequency Identification,” High Frequency Electronics, Part 1, June 2005; Part 2, August 2005.
2. D. Dobkin and S. Weigand, “Environmental Effects on RFID Tag Antennas,” 2005 IEEE MTT-S International Microwave Symposium, paper TU3A-2.
3. V. Pillai, J. Peternel, H. Heinrich, R. Martinez and K.V.S. Rao, “Using Volatile State Storage for Substantial Improvement in RFID Throughput,” Fourth IEEE Workshop on Automatic Identification Advanced Technologies Digest, October 17–18, 2005, pp. 101–105.
4. C. Balanis, Antenna Theory, Third Edition, John Wiley & Sons Inc., Hoboken, NJ, 2005, p. 103.
5. C. Balanis, Antenna Theory, Third Edition, John Wiley & Sons Inc., Hoboken, NJ, 2005, p. 98.
6. http://www.chemsoc.org/exemplarchem/entries/2003/bristol_cook/latticetypes.htm and http://www.matter.org.uk/diffraction/geometry/3D_reciprocal_lattices.htm.