Determining cross-modulation interference is an important factor in the design of a code division multiple access (CDMA) mobile transceiver. The cross-modulation interference level directly affects the performance of the receiver's ability to overcome the spurious interferences, such as what the IS-98¹ calls single tone desensitization.

A few papers have been published, characterizing the cross-modulation caused by the low noise amplifier (LNA) in a receiver front end, from empirical equations to rigorous mathematical derivations.^2-5 The cross-modulation levels characterized by these papers differ by as much as 10 dB. Through a straightforward mathematical concept and a simple mathematical model, this article addresses these differences and presents a result that is in close agreement with the empirical expressions. The expressions derived in this article have been verified through many commercial CDMA handset designs.

Cross-modulation Spectrum

In a mobile phone that utilizes CDMA technology, the transmitter and receiver operate in a full-duplex mode. The transmit (Tx) power will be present at the LNA input subject to the attenuation of the duplexer in front of the LNA. The interference signal in the receive (Rx) band will also be present at the LNA input. The Tx signal cross-modulating with the interference signal produces an interference that falls in the desired Rx signal band.

Since the Tx signal is a spread spectrum, with its signal energy distributed across its signal bandwidth (1.25 MHz), the power spectrum density (PSD) of the Tx power can be assumed to be approximately expressed as a rectangular function, as shown in Figure 1 , where B is the frequency bandwidth of the transmit spectrum.

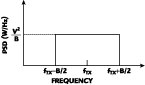
It is known from the Fourier transform that, for a signal to have such a spectrum, the signal in the time domain must be a Sinc function,6

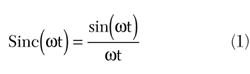
where = 2 f_TX and f_TX is the frequency of the Tx carrier signal. When the Tx signal is present at the LNA input along with an interference signal (one-tone interference signal), the Tx signal is squared by the nonlinearity of the LNA, producing a low frequency (baseband) product that has twice the bandwidth (B) of the original Tx signal. This baseband product has a PSD that is a triangular function because it is a result of the convolution of the rectangular PSD by itself.⁷ Cross-modulation is produced when the baseband Tx product is modulated onto the one-tone interference signal, resulting in a spectrum, as shown in Figure 2 , where f_c is the center frequency of the desired CDMA signal, f_I is the frequency of the interference signal and f = f_I - f_c.

Note that the cross-modulation product of a CDMA signal will not fall completely in the entire band of the desired signal because of the frequency offset ( f), and the cross-modulation product has a bandwidth that is twice the bandwidth of the desired CDMA signal. The PSD of the cross-modulation product may be expressed mathematically as

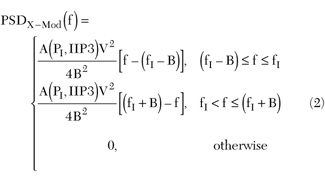
where

A = a function of the interferer power level, P_I

IIP3 = input third-order intercept point of the LNA

The function A describes the nonlinearity of the LNA.

The cross-modulation power that falls in the band of the desired CDMA signal may be calculated from

Let the CDMA cross-modulation factor, C, be the ratio between the cross-modulation power that falls in the desired band and the total cross-modulation power, or

where

assuming unity impedance at the LNA input. In Equation 5, it is also assumed that the LNA distributes the harmonic products of the Tx power with one-half of its harmonic power at the baseband, cross-modulated with the one-tone interference, while the other half power is at its second-harmonic frequency.

Note that the cross-modulation factor, C, is a function of the frequency offset, f, and the channel bandwidth, B. It is not related to the nonlinear characteristics of the device. The frequency offset, f, must be less than 1.5B for the cross-modulation product to fall in the Rx band. C should always be less than unity.

Cross-modulation Power Level

The intermodulation product of single-tone signals may be calculated as⁸

P_(2A-B) = 2P_A + P_B - 2IIP₃ (6)

where

P_A = power level (dBm) of the signal that is squared

P_B = single-tone interference (dBm)

IIP₃ = input third-order intercept point of the nonlinear device (dBm)

All power levels are referred to the input of the device. Note that for a single-tone intermodulation interference, all the interference power falls in the band of the desired signal.

It is easy to demonstrate that intermodulation and cross-modulation are generated by the same nonlinearity, A(P_I,IIP₃), of the LNA. Therefore, Equation 6 also applies for cross-modulation when the cross-modulation product falls entirely on the Rx band.

To apply Equation 4 in the CDMA cross-modulation calculation, let

P_A = P_Tx (7)

P_B = P_I (8)

P_(2A-B) = P_X-Mod(total) = P_X-Mod(in Rx band) - C(dB) (9)

where

Substituting Equations 7 through 9 into Equation 6 gives

P_X-Mod(in Rx band) = 2P_Tx + P_I - 2IIP₃ + C(dB) (11)

As per IS-98¹ and JSTD-18,⁹ the single-tone desensitization is measured with the one-tone interference at 900 kHz and 1.25 MHz offset from the channel frequency for cellular and PCS bands, respectively, or

For cellular band, f = 900 kHz, B = 1.23 MHz, C(dB) = -8.32 dB, or

P_X-Mod(in Rx band) = 2P_Tx + P_I - 2IIP₃ - 8.31 (for cellular band) (12)

For PCS band, f = 1.25 MHz, B = 1.23 MHz, C(dB) = -12.33 dB, or

P_X-Mod(in Rx band) = 2P_Tx + P_I - 2IIP₃ - 12.33 (for PCS band) (13)

Examining Equation 11, note that the cross-modulation interference is reduced by C (dB) because the interference does not occupy the entire Rx band as a result of spectrum spreading that distributes the energy over a frequency band.

Equations 12 and 13 are in close agreement with the empirical equations derived by Draxler²

P_X-Mod(in Rx band) = 1.906P_Tx + 0.949P_I - 1.852IIP₃ - 8.4 (for cellular band) (14)

P_X-Mod(in Rx band) = 1.913P_Tx + 0.949P_I - 1.864IIP₃ - 12.7 (for PCS band) (15)

The empirical equations were derived through a series of discrete time-domain simulations using Omnisys (Agilent Technologies) and curve-fittings with a linear regression. Other references, such as Ali-Ahmad¹⁰, would yield an expression similar to Equation 11, but with C = -3 dB for the cellular band, in which it is assumed that the cross-modulation product is one-half in band and one-half out of band, and hence the 3 dB factor. Such a treatment over estimates the interference contribution due to cross-modulation.

Comparison

As an example, let the Tx power level presented at the input of the LNA be -33.0 dBm, the one-tone interferer be -32.0 dBm and the LNA input IP3 be +9.0 dBm. Table 1 illustrates the cross-modulation levels at the LNA input as calculated from Equations 12 through 15. The difference between the results of this article and the empirical equations are -4.8 and -4.2 percent for the cellular and PCS frequency bands, respectively.

The analysis presented in this article assumes that the cross-modulation power is evenly distributed at the baseband and the second harmonic of the Tx frequency. Also, the nonlinearity higher than the second order has been ignored. Such treatments may under-predict the cross-modulation power level, which accounts for the difference indicated in the data.

Equations 14 and 15 were used to design over 10 different models of CDMA handsets for both cellular and PCS frequency bands. Laboratory tests show that Equations 14 and 15 over estimate the cross-modulation contribution, resulting in a larger design margin than budgeted. Using Equations 12 and 13 will lead to a more accurate system link budget and relax the specifications for the duplexer and LNA, reducing the cost of the CDMA handsets.

References

1. Recommended Minimum Performance Standards for Dual-mode Spread Spectrum Cellular Mobile Stations, TIA/EIA/IS-98-B Standard, Section 9.4.2., August 1998.
2. P. Draxler, private e-mail communication, Qualcomm Inc., July 23, 1997.
3. R. Mohindra, "Part 1: Cross-modulation and Linearization in CDMA Mobile Phone Transceivers," Wireless Symposium/ Portable by Design Conference Digest , San Jose, CA, 1999.
4. V. Aparin, B. Butler and P. Draxler, "Cross-modulation Distortion in CDMA Receivers," IEEE Transactions on Microwave Theory and Techniques , Vol. 48, No. 12, December 2000, pp. 100-109.
5. "The Effect of CDMA Receiver Minimum Standards on RF Systems," Application Notes, Maxim Integrated Products Inc., September 2000.
6. J.D. Gaskill, Linear Systems, Fourier Transforms and Optics , John Wiley & Sons Inc., New York, NY 1978.
7. E.O. Brigham, The Fast Fourier Transform and Its Applications , Prentice-Hall Inc., Englewood Cliffs, NJ 1988, pp. 60-65.
8. H. Kinley, "More About Intermodulation," Mobile Radio Technology , April 1995, p. 8.
9. Recommended Minimum Performance Requirements for 1.8 to 2.0 GHz Code Division Multiple Access Personal Stations, TIA/EIA/J-STD-018 Interim Standard, Section 3.4.2, January 1996.
10. W.Y. Ali-Ahmad, "RF System Issues Related to CDMA Receiver Specifications," RF Design , September 1999.

Yang Zhang received his BSEE degree (with high honors) from China University of Electronics Science & Technology, Chengdu, China, in 1982, and his MS and PhD degrees in electrical engineering from Duke University, Durham, NC, in 1984 and 1990, respectively. Since 1990, he has worked with Duke University as a research associate, conducting research in microwave-induced hyperthermia for cancer treatment; Otsuka Electronics, Fort Collins, CO, as a principal engineer, developing transceivers for MRI systems; and Ericsson Inc., Lynchburg, VA, as a receiver special team leader, leading a group of engineers to design land mobile radios and base stations. Zhang joined Qualcomm Inc. in 1996, and is currently a principal engineer, leading a team of engineers designing various 2G and 3G CDMA handsets of multiple modes and frequency bands. He has designed over 10 different models of CDMA cell phones marketed in both North America and China. Zhang has authored more than 30 technical papers and holds two US patents. He can be reached at (858) 651-8741 or via e-mail at yzhang@qualcomm.com.