Successful microwave circuit realization requires flexible circuit analysis tools that allow engineers to prototype, analyze and verify their circuits. Today, available software tools offer standard features such as frequency analysis, tuning and optimization, but are differentiated by their model libraries and special customization capabilities.

This article describes the design of interdigital microstrip filters using the MMICAD Linear Simulator.¹ Interdigital microstrip filters with tapped-line input are compact structures suitable for microwave integrated circuits. Their advantages include low levels of spurious second harmonic passbands and relatively low cost. This article shows how MMICAD can be used for the full filter design cycle, encompassing specification, basic equations, parameter calculations, simulation and optimization. The final design is verified using the Sonnet electromagnetic simulator.²

The general schematic of an N-conductor filter is shown in Figure 1 . These filters are characterized by:

• Two impedance transforming elements at each periphery
• Quarter-wave coupled line resonators between the impedance transformers
• Alternating ends of the resonators shorted to ground using vias, with the other ends open
• Microstrip lines tapped in precise points at θ _T
• Shunt capacitances C^S at either end of the impedance transforming elements (to aid the resonance condition)

Several design variations of this filter exist that involve different resonator line impedances and adjustment of individual resonator widths and gaps. From the filter order N, center frequency f₀ and bandwidth w, the low pass filter prototype coefficients g_j can be obtained. Using these parameters and the resonator impedance Z_s, the fundamental design equations for the resonator length θ ₁, tap length θ _T, C_S, and the even and odd impedances Z_oej and Z_ooj of the resonators can be calculated, as outlined by Caspi and Adelman₃ and shown in Table 1 .

One problem of simulating this filter with currently available CAD tools is either the absence of a multiple coupled microstrip line model, or the difficulty of specifying arbitrary tap points in multiple coupled line models; the input/output points are usually at the resonator ends. However, the filter can be simulated using multiple single coupled lines (see the procedure outlined by Grayzel).⁴ This procedure restricts the physical filter topology to one where line widths and impedances are the same, while the gaps are allowed to vary, as shown in the equivalent circuit of Figure 2 .

The CAD approach simulates the physical structure of the original schematic. Given that the resonator line impedance is Z_s, the first coupled resonator is simulated by the physical coupled line model, CLINP, which is characterized by even- and odd-mode impedances and even- and odd-mode effective dielectric constants as parameters. These parameters are related to those of the physical structure by the following transformation:

(1)

Z' _oe1 = 1/(1/Z _oe1 -1/2Z _s )
Z' _oo1 = 1/(1/Z _oo1 -1/2Z _s )
k' _oe1 = k _oe1
k' _oo1 = k _oo1

The simulated even and odd dielectric constants, k_oe1 and k_oo1, are the same as those of the physical structure. The second and following resonators are simulated in the same manner. Simulation of the final coupled resonator also uses the physical coupled line model whose odd- and even-mode impedances are related to the physical structure by the following transformation:

(2)

Z' _oeN = 1/(1/Z _oeN -1/2Z _s )
Z' _ooN = 1/(1/Z _ooN -1/2Z _s )
k' _oeN = k _oeN
k' _ooN = k _ooN

It is necessary to add a physical transmission line model, TLINP, at either end of the filter. TLINP is characterized by impedance and effective dielectric constant. It simulates the actual structure by the following transformation:

(3)

Z' _s = 2Z _s
k' _eff = k _eff

The choice of Z_s allows the designer to synthesize the conductor widths and calculate the effective dielectric constant. The impedance can be selected as long as all conductor widths are set to correspond to the same impedance value. Once the even- and odd-mode impedances are determined, and knowing the conductor width, the coupled line gaps, S_1...4, and the even- and odd-mode effective dielectric constants, k_oe1...4 and k_oo1...4, can be synthesized.

Finally, the actual resonator length, L₁, is obtained by noting that at the midband frequency⁵

(4)

β L ₁ = θ ₁

where

β = propagation constant

(5)

β = 2π: /λ

λ is related to the center frequency, f₀, and the effective dielectric constant of the substrate k_reff, such that

The effective dielectric constant can also be considered as the geometric mean of the even- and odd-mode dielectric constants:

Finally, the expression for the resonator length is obtained as

The tap length L_T can then be related to L₁ in the same manner as θ _T to θ ₁. This completes the set of equations required for use in the CAD program.

Filter Design Example

In this example, the following bandpass interdigital filter is specified:

f₀ = center frequency = 5.1 GHz,
w = bandwidth = 340 MHz,
N = number of poles = 5

The filter will use a substrate with a dielectric constant of 9.8 and a thickness of 15 mils, with 1 mil thick gold metallization. One of the design options is to select the resonator impedance, Z_s, which is chosen to be 50 Ω . The conductor widths, W_1...5, will be fixed to respond to the same impedance.

As a first design step, the low pass prototype element values, g_o to g₅, are obtained. These can be obtained using handbooks or the equation in Vizmuller.⁶ The filter design tool incorporated in the MMICAD linear simulator is used to provide these values.

The following characteristics are specified:

• Normalized low pass filter
• Chebychev filter response
• Maximum passband ripple 0.1 dB
• Source and load impedances of 50 Ω

Figure 3 shows the MMICAD input display.

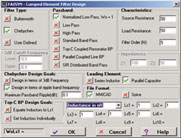
The program returns a circuit network list of a fifth-order LC filter with the following normalized values:

g_o = 1.000000, g₁ = 1.146812,
g₂ = 1.371213, g₃ = 1.975003,
g₄ = 1.371214, g₅ = 1.146818

The filter design equations of Table 1 can now be calculated using MMICAD equation entries in Procedure mode and Parameter sweep modes. Whenever non-frequency analysis is required, such as in this case, the parameter sweep is invoked to allow MMICAD to operate as a math solver. Output blocks tabulate the resulting calculations (note: actual network list circuit files have not been included but are available from the author). Analyzing the netlist file generates the following outputs:

(9)

θ ₁ = 1.52 radians or 87.00°
θ _T = 0.22 or 12.75°
C _S = 0.00627 pF
Z _oe1 = Z _oe4 = 52.18 Ω
Z _oo1 = Z _oo4 = 48.00 Ω
Z _oe2 = Z _oe3 = 51.64 Ω
Z _oo1 = Z _oo4 = 48.46 Ω

The resonator's line widths are then determined. The resonator impedance is initially set to 50 Ω . In addition, the substrate and dielectric constant are selected. This allows calculation of the resonator width, W_1...5 = W, and the microstrip line effective dielectric constant, k_eff. MMICAD optimization is used to calculate these parameters with the following partial network listing shown in Table 2 .

In this listing, two circuit elements, the physical transmission line, TLINP and the dispersive microstrip line model, MTRL, are equated by optimization. The S-parameters of the TLINP element must be the same as that of MTRL. While doing so, the line width and effective dielectric constant are varied until the impedance is 50 Ω . Optimization in this case is difficult since parameters are varied simultaneously in two models. This is accomplished by (1) selecting the starting value of line width to be the same as the dielectric thickness, 15 mils (this is a first-order approximation given that the required line impedance is 50 Ω ); and (2) bounding the line impedance optimization tightly allowing it to vary only between 49.99 to 50.01 Ω . The first round of optimization generates the following final results:

(10)

W _1...5 = 14.55 mils
Z _s = 49.99 Ω
k _eff = 6.63

The coupled line gaps, S_1...4, and the even- and odd-mode effective dielectric constants, k_oe1...4 and k_oo1...4, can now be calculated using MMICAD coupled line synthesis (note: the actual netlist is available from the author).

In this listing, the coupled line parameters are synthesized by forcing the S-parameters of the physical transmission line, CLINP, to be equal to that of the dispersive microstrip coupled line model, MCLIN. For a constant line length, the CLINP's S-parameters must be equated to the MCLINs. In the process, the even and odd dielectric constants as well as the line gap are determined. Optimization at the midband frequency yields

(11)

W ₁ = W ₄ = 14.54 mils
W ₂ = W ₃ = 14.54 mils
S ₁ = S ₄ = 38.63 mils
S ₂ = S ₃ = 46.21 mils
k _e1 = k _e4 = 7.00
k _o1 = k _o4 = 6.25
k _e2 = k _e3 = 6.94
k _o2 = k _o3 = 6.32

This procedure provides the data to calculate both the resonator length and tap length:

Resonator lengths = L_1...5 = 217.41 mils
Resonator tap length = L_T = 31.86

which completes the filter design equations.

Filter Simulation in MMICAD

Linear analysis of the filter and evaluation of the S-parameter response involves compilation of the MMICAD circuit file (due to its length, this circuit file is not shown but is available from the author).

The netlist includes a "HALF" two-port network in the circuit block. The symmetry of the circuit is taken into account. Included in this two-port network are one TLINP element, two coupled line resonators, and one resonating capacitance Cs. Small shorting inductances and open capacitances are used to simulate parasitics at the resonator terminations. For the final two-port network, MMICAD joins the two HALFs and completes the filter circuit by adding parasitics at the interface. The S-parameters of the resulting circuit are shown in Figure 4 .

In this simulation, a minor optimization to center the frequency response at 5.1 GHz and obtain an input reflection coefficient, S₁₁, better than -15 dB, was performed.

The finalized variables are resonator length = L_1...5 from 217.41 to 218.5 mils, resonator tap length = L_T from 31.86 to 31.30 mils and C_S from 0.0063 to 0.013 pF. The insertion loss of this filter varies between slightly better than 3 dB, to 4 dB at the band edges.

Filter Simulation in Sonnet

The same filter was also simulated using the Sonnet Lite electromagnetic simulator. Sonnet performs its analysis using the modified method of moments. The EM analysis should independently verify the filter design equations and the MMICAD simulations. The layout is shown in Figure 5 .

Initial layout in Sonnet used the same dimensions as the MMICAD analysis starting with an 0.5 mil square grid. The Sonnet Lite 16 Mbits analysis memory restriction necessitated moving to a 2 mil square grid. The results obtained for the coarser grid were box dimensions 374 x 216 mils, resonator widths W_1...5 = 14 mils, gaps S₁ = S₄ = 38 mils and S₂ = S₃ = 46 mils, resonator length L_1...5 = 214 mils and tap length L_T = 32 mils. Furthermore, an open microstrip of width 14 mils and length 4 mils was substituted for the resonating capacitance C_s (these microstrip dimensions were arrived at using purely geometrical considerations of metallization area over a substrate). The shorted ends of the resonators are simulated by attaching these ends to the box walls, which are perfect grounds in Sonnet. Finally, 50 Ω lines with tapers were used to attach the input/output ports to the taps of the filter. The resulting frequency response of the lossless circuit compared to MMICAD simulation is shown in Figure 6 .

Conclusion

The filter passband shows good agreement. The insertion loss is higher in MMICAD since the simulation in Sonnet Lite was performed with lossless metallization. The input reflection coefficient in MMICAD tracks Sonnet Lite reasonably well, although the five filter poles are well resolved in Sonnet Lite. This comparison confirms the validity of the interdigital filter design.

A classical design approach to a popular microwave circuit, combining design equations and simulation tools, was demonstrated in this article. The circuit files used can be retained in a library to accommodate filter redesigns with other frequency responses.

Philip Dindo may be reached at the Herzberg Institute of Astophysics, National Research Council Canada, 5071 W. Saanich Road, Victoria, BC V9E 2E7 or via e-mail at philip.dindo@nrc.ca.

References

1. MMICAD Linear Simulator, Optotek Ltd., 62 Steacie Drive, Ottawa, ON K2K 2A9, Canada.
2. Sonnet Software Inc., 1020 Seventy North Street, Liverpool, NY 13088.
3. S. Caspi and J. Adelman, "Design of Combline and Interdigital Filters with Tapped-line Input," IEEE Transactions on Microwave Theory and Techniques , Vol. 36, April 1988, pp. 759-763.
4. A.J. Grayzel, "A Useful Identity for the Analysis of a Class of Coupled Transmission Line Structures," IEEE Transactions on Microwave Theory and Techniques , Vol. 22, October 1974, pp. 904-906.
5. M. Krage and G. Haddad, "Characteristics of Coupled Microstrip Lines II: Coupled-mode Formulation of Inhomogeneous Lines," IEEE Transactions on Microwave Theory and Techniques , Vol. 18, April 1970, pp. 222-228.
6. P. Vizmuller, RF Design Guide: Systems, Circuits and Equations , Artech House Inc., Norwood, MA, pp. 109-113.