Increasing demand for higher data rates and channel capacity is driving the need to use the RF spectrum more efficiently. As a result, 5G wireless systems will use mmWave frequency bands to take advantage of the increased bandwidth. The higher operating frequencies enable large-scale antenna arrays, which can be used to mitigate severe propagation loss in the mmWave band. Large arrays can also be used to implement a MIMO system in which unique signals can be transmitted from different antenna elements in the array. MIMO systems enable spatial multiplexing techniques that can be used to improve data throughput.
The core idea of spatial multiplexing is to create multiple subchannels in scatterer-rich environments so that multiple data streams can be transmitted and recovered independently. This is achieved by applying a set of precoding and combining weights derived from the channel matrix. This concept is discussed first with an all-digital solution based on precoding in a MIMO-OFDM system that uses a spatial channel model. This channel model incorporates array pattern information to improve model fidelity.
Because 5G systems require large antenna arrays, applying digital weights on each antenna element is not always practical due to cost and space limitations. Hybrid beamforming techniques can be applied in a mixed RF and digital beamforming system to alleviate these restrictions. In a hybrid beamforming system, both the precoding weights and the combining weights are combinations of baseband digital weights and RF band analog weights. On the transmit side, the baseband digital weights modulate the incoming data streams to form input signals at each RF chain, and the analog weights then translate the signal at each RF chain to the signal radiated at each antenna element. The process is reversed on the receive side. This article includes an example with hybrid weights and compares the achieved spectral efficiency with the all-digital case.
SPATIAL MULTIPLEXING
The idea behind spatial multiplexing is that a MIMO system in a multipath channel with a rich scatterer environment can send multiple data streams simultaneously across the channel. For example, the channel matrix of a 4 × 4 MIMO channel becomes full rank because of the scatterers. This means that it is possible to send as many as four data streams at once. The goal of spatial multiplexing is less about increasing the signal-to-noise ratio (SNR) and more about increasing the information throughput.
The idea of spatial multiplexing is to separate the channel matrix into multiple modes so that the data stream sent from different elements in the transmit array can be independently recovered from the received signal. To achieve this, the data stream is precoded before the transmission and then combined after the reception. In the MATLAB models that follow, the precoding and combining weights can be computed from the channel matrix by:
[wp, wc] = diagbfweights(mimompchan);
The information received by each receive array element is simply a scaled version of the transmit array element, which results in multiple orthogonal subchannels within the original channel. The first subchannel corresponds to the dominant transmit and receive directions, so there is no loss in the diversity gain. In addition, it is possible to use other subchannels to carry information, as shown by the bit error rate (BER) curves in Figure 1, including the first two subchannels. The gain of the second data stream is not as high as the first stream, since it uses a less dominant subchannel. Still, the overall information throughput is improved. This concept will be applied to a MIMO-OFDM system.
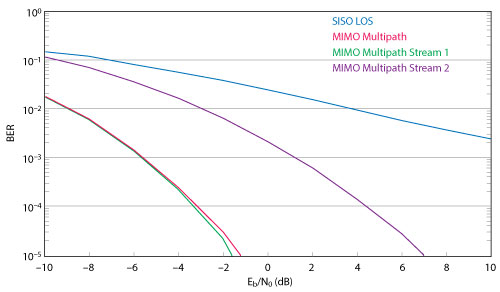
Figure 1 BER of MIMO multipath streams compared to a single line-of-sight link.
MIMO-OFDM SYSTEMS
MIMO-OFDM systems are common in wireless systems due to their robustness with frequency-selective channels and high data rates. With antenna arrays that implement spatial multiplexing, efficient techniques to realize the transmissions are necessary. As an example, consider an asymmetric MIMO-OFDM single-user system in which the maximum number of antenna elements on the transmit and receive ends are 1024 and 32, respectively, and up to 16 independent data streams. For clarity, a single link (one base station communicating with one mobile user) is modeled, but this structure could be extended for more complex configurations.
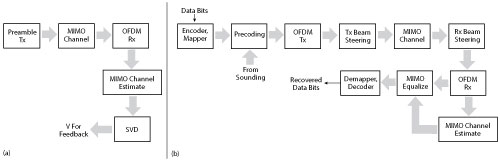
Figure 2 Channel sounding (a) and data transmission/reception (b) flow.
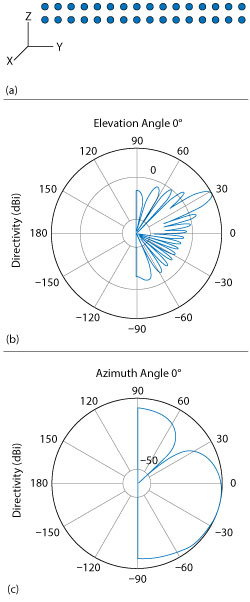
Figure 3 Transmitter array geometry (a) with azimuth (b) and elevation (c) beam patterns.
The link between the transmitter and receiver relies on channel sounding to generate the channel information needed for transmit beamforming. For a spatially multiplexed system, the availability of channel information at the transmitter allows for precoding to be applied to maximize the signal energy in the direction and channel of interest. Assuming a slowly varying channel, this process is facilitated by first sounding the channel with a reference transmission. The receiver then estimates the channel and feeds this information back to the transmitter, as shown in Figure 2. In this system, a preamble signal is first sent over all transmitting elements. It is subsequently processed at the receiver after accounting for the channel effects. The receiver performs pre-amplification, OFDM demodulation, frequency domain channel estimation and calculation of the feedback weights based on channel diagonalization using singular value decomposition per data subcarrier. The specific system configuration is as follows:
| % Single-user system with multiple streams | |
| prm.numSTS = 16; | % Number of independent data streams, 4/8/16/32/64 |
| prm.numTx = 32; | % Number of transmit antennas |
| prm.numRx = 16; | % Number of receive antennas |
| prm.bitsPerSubCarrier = 6; | % 2: QPSK, 4: 16-QAM, 6: 64-QAM, 8: 256-QAM |
| prm.numDataSymbols = 10; | % Number of OFDM data symbols |
A rectangular array at the transmitter is used, based on the desired number of data streams and transmit antennas. Figure 3 shows the array geometry of the transmitter and the beam patterns in azimuth and elevation. For simplicity, assume the steering angle is known with respect to the mobile location. In actual systems, the steering angle would be obtained from an angle-of-arrival estimation at the receiver, as a part of the channel sounding or initial beam tracking procedures.
Multiple options exist for modeling spatial MIMO channels, typically selected based on the level of fidelity that is needed for the analysis. For example, 5G channel models and the WINNER II channel models are spatially defined MIMO channels where the array geometry and location information can be specified. For this discussion, consider scattering-based channels with a single-bounce path through 100 scatterers placed randomly within a circle between the transmitter and receiver. The channel model allows path loss modeling and both line-of-sight (LOS) and non-LOS propagation conditions. For this analysis, a non-LOS propagation and isotropic antenna element pattern with linear geometry are configured. The same channel is used for both sounding and data transmission. The data transmission has a longer duration controlled by the number of data symbols.
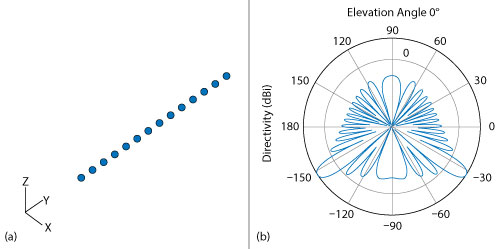
Figure 4 Receiver array geometry (a) with azimuth beam pattern (b).
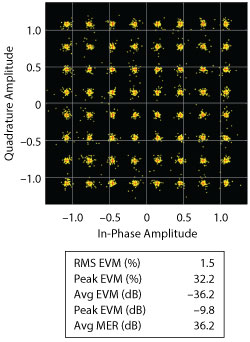
Figure 5 Constellation diagram for the MIMO OFDM system.
The receive antenna array, shown in Figure 4, passes the propagated signal to the receiver to recover the original information embedded in the signal. Similar to the transmitter, the receiver used in a MIMO-OFDM system contains many stages, including OFDM demodulator, MIMO equalizer, QAM demodulator and channel decoder. For this MIMO system, the displayed receive constellation of the equalized symbols offers a qualitative assessment of the reception. The actual BER offers the quantitative figure by comparing the actual transmitted bits with the received decoded bits (see Figure 5).
Parameters can be modified to vary the number of data streams, transmit/receive antenna elements, base station or array locations and geometry, channel models and their configurations to study the parameters’ individual or combined effects on the system. This framework can be used for further analysis but, so far, all of the precoding and combining were based on an all-digital system. As the antenna array size increases, an all-digital system may not be feasible, which leads to the use of hybrid beamforming.
