Figure 1 In range gate pull off, large jammer pulses move away from the smaller radar reflection signal and then vanish.
A pilot’s ability to maneuver out of harm’s way depends on the seconds that elapse between detection, identification of an enemy missile’s radar signal and the jamming response from the aircraft’s electronic attack (EA) system. A designer’s confidence in the integrity of that EA system is based, in part, on the ability to capture related RF signals using measurement equipment with sufficient dynamic range, instantaneous bandwidth and capture time to validate the radar/jammer signal interaction. These tests are often performed in a lab environment. This article describes digitizer capture methods, including raw and digital down-conversion (DDC), comparing the key trade-offs for making essential validation measurements: dynamic range, bandwidth and capture time.
One basic jamming technique is called range gate pull off (RGPO). The idea is that an EA system aboard an aircraft reacts to the received radar tracking pulses by creating and sending jamming pulses back to the radar. The goal is to deceive the radar and cause it to break range tracking, so it is unable to launch a surface-to-air missile (SAM). Or, if a missile is launched, the goal is to cause the radar to break range tracking in such a way that the missile veers off its target and is unable to harm the war fighter and aircraft. With RGPO, large jammer pulses are first placed “on top” of the radar skin return pulses at the radar receiver; then, the jammer pulses “walk away” from the radar skin return pulses, causing the radar range gates to follow the jammer pulses instead of the real radar reflection. Finally, the jammer pulses vanish, causing the radar to lose the range of the target (see Figure 1).
When designing a radar RGPO jamming system, several SAM radar parameters must be understood for the EA to be effective. These include:
- FM chirp of the particular modulation width
- Carrier frequency and whether it hops
- Pulse repetition interval (PRI) and whether it dithers
- Pulse width
- Transmit power
- Antenna boresight gain.
While the missile’s travel time and distance to a possible target vary across scenarios, these are also important to consider. A reasonable example is that a missile could take approximately 20 s to reach a target
10 km distant.
An important step when designing RGPO jamming systems is considering the expected radar skin return signal at the radar receiver. The jammer is then designed to create signals 6 to 20 dB larger in amplitude. The open literature describes the derivation and use of the radar range equation and calculations of skin return power levels. Several factors are part of the calculation, and simple equations have been developed for easy calculation of the power level in dBm.1
S = ‐103 + ERPr − 40log(R) − 20log(F) + 40log(σ) + G
where
S = Skin return power at the radar receiver in dBm
ERPr = radar effective radiated power toward the target
R = range from the radar to the target in km
F = radar transmitting frequency in MHz
σ = radar cross section of the target in m2
G = main beam boresight gain of the radar antenna in dB
The formula contains a constant, ‐103, which combines various conversion factors, allowing inputs for the variables to be in the most convenient units.
As an example, consider the return signal level from a target 10 km from the radar, with the radar’s carrier frequency at 3 GHz. Typical values found in the open literature are used for the other factors or derived from related information found in the literature. Calculations based on a range of typical values yield power levels from around ‐45 to ‐65 dBm at the SAM tracking radar receiver. Jammer pulses would be designed to be up to 20 dB stronger at the radar receiver; with the skin return pulses at ‐65 dBm, the jammer pulses would need to be at ‐45 dBm.
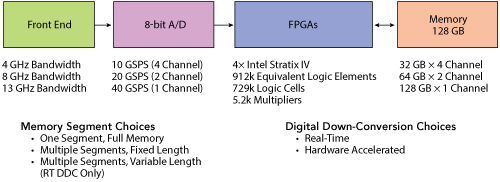
Figure 2 Wideband 8-bit digitizer technology.
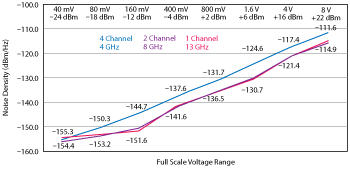
Figure 3 Noise density for 4, 8 and 13 GHz bandwidth digitizers.
USING A DIGITIZER
Can a digitizer be used to measure the signals to validate a jammer? The answer is “it depends.” Answering the question requires evaluating the trade-offs among bandwidth, sensitivity and the target time during which the pulses need to be captured. For this example, in addition to having a
3 GHz carrier, assume the radar and jamming signals have a 40 MHz wide FM chirp modulation, with a 1 µsec pulse width and 10 kHz PRI. It is helpful to observe a handful of RGPO jamming cycles, where the jamming pulses walk the radar range gates away from the real radar reflection pulses. Each RGPO cycle lasts around 10 s, so it is important to capture, observe and analyze the radar skin return and jammer pulses for about 60 s.
Modulation bandwidth, pulse width, PRI and total pulse capture time are factors that determine whether a digitizer can measure such pulses for EA validation. The digitizer technology, shown in Figure 2, can achieve the bandwidths, sample rates and FPGA processing power for signal processing like DDC, which will be instrumental in achieving the desired 60 s pulse capture period. Another key digitizer capability is noise density and the sensitivity possible when using various digitizer models and capture modes. When operated at full bandwidth, each digitizer model has a certain rms noise level for each sensitivity setting. These rms noise levels can be converted into power levels in dBm, then scaled to a 1 Hz measurement bandwidth using the following calculation:
Noise density (dBm/Hz)= 20log ((Vrms * 2.83Vpp/Vrms)/0.632Vpp) − 10log(Full Bandwidth)
This is handy, since 1 Hz measurement bandwidth noise density values can easily be converted into noise levels for any desired measurement bandwidth. The noise density for three digitizer models is shown in Figure 3.
In the example where the radar and jammer pulses have a 3 GHz carrier and are 40 MHz wide, a 4 GHz model digitizer can be used to sample the signals. Since both radar and jamming pulses need to be measured, the sensitivity must allow the input range to be larger than the ‐45 dBm jammer pulse level, to prevent the jammer pulses from being clipped. That allows the highest sensitivity of 40 mV full scale to be used with its corresponding
‐155.3 dBm/Hz noise density. Calculating the noise that would be present if the full 4 GHz bandwidth was used:
Noise dBm (Measurement Bandwidth Span) = Noise Density + 10log(Measurement Bandwidth Span)
For the example, at 40 mV full scale using a 4 GHz system at full bandwidth:
Noise dBm (@ 4 GHz Span) = ‐155.3 dBm + 10log(4 × 109) = ‐155.3 dBm + 96 dB = ‐59.3 dBm.
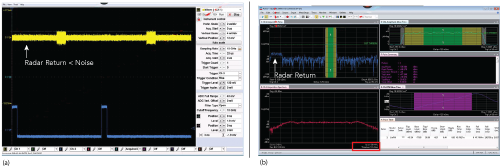
Figure 4 With 4 GHz digitizer bandwidth, noise obscures the radar skin return (a). Using digital down-conversion to reduce the bandwidth to 50 MHz, both the radar skin return and jammer pulses are visible (b).
So, at a full 4 GHz bandwidth, the noise would be greater than the ‐65 dBm radar reflection pulse. This is where DDC comes into play. The signals only had a 40 MHz FM chirp spectral width, so DDC can be used to reduce the measurement span to something slightly wider than the signals. 50 MHz would work well. Considering the noise level in a 50 MHz measurement bandwidth at 8 mV full scale and using a 4 GHz system:
Noise dBm (@ 50 MHz span) = ‐155.3 dBm + 10log(0.05 × 109) = ‐155.3 dBm + 76.9 dB = ‐78.3 dBm
Theoretically, the noise would now be less than the ‐65 dBm radar skin return.
A measurement can prove this. Radar skin return and jammer signals can be emulated using an arbitrary waveform generator driving the wideband I/Q inputs of a vector signal generator, with measurements at the full 4 GHz bandwidth and then with a 50 MHz span (see Figure 4).
HOW MUCH DATA?
After showing that a digitizer can be used to measure the signals necessary to validate a jammer, the next question is whether every radar and jammer pulse can be captured over the 60 s period. Again, the answer is “it depends.” The 4 GHz bandwidth digitizer running at 10 GSPS and with 30 GB of memory available for capture equates to only 3 s of capture time. Two ways to increase the time over which pulses are captured are using segmented memory and DDC.
The RGPO example uses jammer pulses that walk away from radar reflection pulses for about a 10 µs period, then vanish for a few seconds until the radar gains range lock again. Then the jammer starts walking jammer pulses away from the radar reflection pulses. By using a capture mode called segmented memory, where capture begins with a trigger event and samples are captured for a fixed period, it is possible to capture the radar and jammer pulses as they interact. Capture is then turned off during the long period where no pulses are present during the 100 µs PRI. With a raw 10 GSPS capture and 100 ps sample point spacing, where 15/16 of the on-board 32 GB memory is available, the time that the digitizer can capture pulses is calculated as follows:
# segments = (30 GB/10 GSPS)/(12 µs/segment) = 250k segments
Time = 250k segments × 100 µs PRI = 25 s
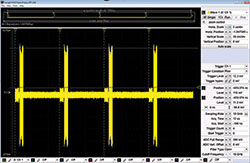
Figure 5 Raw 10 GSPS capture with 12 µsec wide segments and 4 GHz digitizer bandwidth.
Over a 25 s period, one could see a couple RGPO cycles, but not the desired 60 s of engagement. There is also the issue of the high noise level using the full 4 GHz of bandwidth. Figure 5 shows a capture using segmented memory and 12 µs segments, but with much larger input signals than previously calculated for the radar reflection and jammer pulses. With the signal levels expected at the radar receiver, the digitizer noise would have obscured the small radar reflection signals.
A feature called real-time DDC can narrow the span to both reduce noise and greatly utilize the memory by storing the I and Q data with a much lower sample rate than the original 10 GSPS voltage point samples. Using 50 MHz of instantaneous bandwidth to capture the 40 MHz wide signals, the 10 GSPS captured data is processed immediately by the FPGAs into 62.5 MSPS I and 62.5 MSPS Q data (125 MSPS total), resulting in 16 ns spaced I and Q sample pairs. The capture time is calculated as follows, knowing that with real-time DDC, one half of the digitizer on-board memory is available for I/Q samples:
Continuous capture = ((1/2)*(32 × 109 samples))/125 × 106 samples/s = 128 s
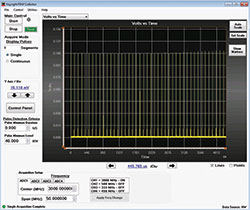
Figure 6 Single segment capture using real-time DDC with a 50 MHz span.
Figure 6 shows a single 400 ms segment of a 50 MHz wide real-time DDC capture.
Newer radars are using wider chirp bandwidths. If the radar has a 450 MHz wide chirp, and the measurement span is increased to accommodate this, then the capture time will scale by the ratio of the 50 and 450 MHz bandwidths, or roughly 10:1. So pulses will only be captured over a 13 s period. By using real-time DDC plus segmented memory, capturing RF pulses over the desired 60 s period would be possible with up to 488 MHz instantaneous bandwidth, limited primarily by FPGA processing power. In fact, pulses could be captured over a 100 s period:
# segments = (½ * 32 GB/1.25 GSPS)/(12 µs/segment) = 12.8 s/(12 µs/segment) ≥ 1M segments
With a 100 µs radar PRI, the total time over which pulses are captured is
1M segments * 100 µs/segment = 100 s
But nothing comes for free. At this wider 488 MHz measurement bandwidth, it may again become difficult to pull weak ‐65 dBm radar reflection pulses out of the higher noise level.
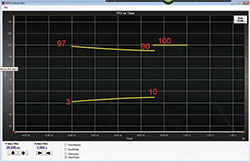
Figure 7 Proper RGPO radar to jammer pulse timing relationships plotted and verified.
A measurement of radar reflection and jammer pulses is shown in Figure 7, where every radar/jammer pulse pair is placed into 12 µs long segments over a 10 s period, and PRI timing relationships are calculated and plotted to verify RGPO operation over that time. The number of segments is set to 100,000 to capture every pulse over a 10 s period (100,000 × 100 µs PRI = 10 s). A logical graph of the PRI calculations is shown, with a resultant PRI curve that changes from 3 to 10 µs in the bottom trace, as the jammer pulses pull away from the radar pulses. Then a fixed 100 µs PRI is seen once the jammer pulses disappear and only the radar pulses are present. This 10 s capture period began slightly after the radar and jammer pulses had already separated by a few µs.
The real-time DDC mode has the further advantage that data can be streamed to an external RAID array, only limiting the time capture by the size of RAID array. In cases where input signals go beyond the DC to 4 GHz input range of the four channel digitizer model, DDC is still possible on 8 and 13 GHz bandwidth models using hardware-accelerated DDC. For applications where a DDC measurement is needed with greater than the 488 MHz instantaneous bandwidth offered with real-time DDC, hardware-accelerated DDC is an option. Hardware-accelerated DDC can be used with 4, 8 and 13 GHz bandwidth digitizers and offers higher measurement bandwidth span settings, up to 1.9, 3.9 and 7.8 GHz, respectively. Hardware-accelerated DDC can also be used to speed up DDC processing when using vector signal analyzer software. But hardware-accelerated DDC has a drawback: it cannot be streamed to RAID, limiting the capture of I/Q samples to the digitizer’s on-board memory.
Summary
We have seen how several tools are valuable for the EA designer who desires to make measurements on radar and jammer signals and the interaction of those signals during an RGPO engagement. RGPO is just one example of a jamming methodology. There are many types of radar electronic protection and EA methods that drive decisions related to the trade-offs discussed for system validation measurements.
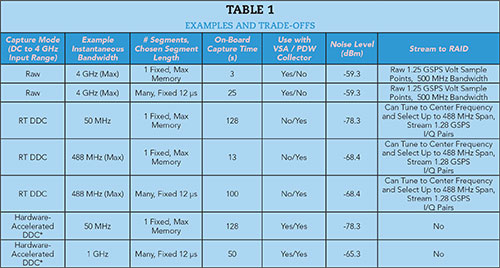
Wideband 8-bit digitizers can be valuable in the collection of radar and jammer pulses for system validation, as well as measuring a host of other electronic warfare signals. Trade-offs are between measurement bandwidth and the total time radar and jammer pulses can be captured. These trade-offs affect the noise present in the measurements, which determines whether small signals like radar reflection pulses can be captured and analyzed. Table 1 summarizes the examples and the trade-offs discussed. A combination of DDC and segmented memory is important for these measurements, which are often performed in a controlled lab environment.
Reference
- David L. Adamy, “EW 104: Electronic Warfare Against a New Generation of Threats,” Artech House Publishers, 2015, pp. 60.

