
Figure 1 Test fixture (a) and network analyzer (b) used to measure large signal S-parameters.
Noise analysis of oscillators, also known as autonomous circuits, was a dream for many years. The first and linear approach must be credited to David Leeson, who took a linear lowpass equivalent circuit and derived his frequently quoted linear formula.1 This formula requires data which can only be gained after a post prior analysis. The values of the output power, the loaded Q, the large-signal noise factor—frequently confused with noise figure (NF), which is 10log(noise factor)—and the flicker noise contribution are not known a priori, although they may be computed.2 The introduction of nodal noise analysis in a proper way was published by Hillbrand and Russer.3 The Lee-Hajimiri noise analysis is interesting but not very practical; while often quoted in the literature, its use is not practically shown.2,4-6 If we combine the Leeson formula with the tuning diode contribution, the following equation allows us to completely calculate the noise of the oscillator.2 The VCO term was added by Rohde,2 and the flicker term was added by Scherer.7
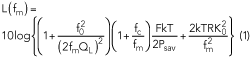
where
L(fm) = ratio of sideband power in a 1 Hz bandwidth at fm to total power, in dB
fm = frequency offset
f0 = center frequency
fc = flicker frequency
QL = loaded Q of the tuned circuit
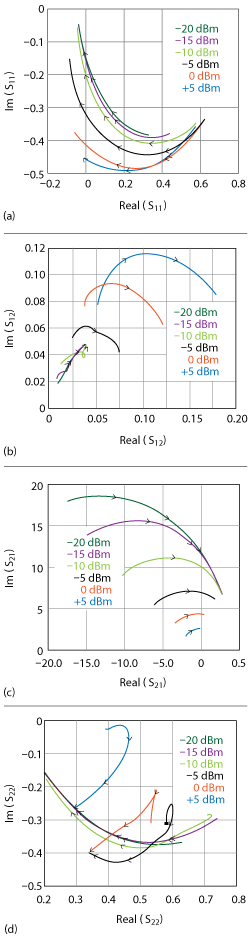
Figure 2 Measured large-signal S-parameters of the Infineon BFP520 bipolar transistor from 600 MHz to 3 GHz in 50 MHz steps: S11 (a), S12 (b), S21 (c) and S22 (d).
F = noise factor
kT = 4.1 × 10-21 at 300K0 (room temperature)
Psav = average output power of the oscillator
R = equivalent noise resistance of the tuning diode (typically 50 to 10 kΩ)
Ko = oscillator voltage gain
Kaertner’s paper8 used a nice time domain approach and includes, probably for the first time, the noise correlation in oscillator design. At that time, the now available harmonic balance method had not been invented. A very good description is found in the works by Rizzoli.9-11 While not easy to read and highly mathematical, Kaertner’s calculation produced real results.
Large-Signal Noise Analysis
The introduction of the piecewise linear harmonic balance (HB) method, developed by Vittorio Rizzoli and his team, was the perfect body to include the noise correlation method. The famous nonlinear time domain circuit analysis program SPICE lacks a rigorous noise correlation analysis, and the HB programs are a hybrid of linear (frequency) and nonlinear (time domain) computations.12,13 Both publications by Rizzoli and Gilmore were leading on the topic. Rowan Gilmore worked with me during our Compact Software time.
My team at Compact Software and the Rizzoli team were struggling to validate the results, and it was complicated to get reliable measured data and maintain accuracy and speed. The Compact Software approach and the Rizzoli team were always fighting about this topic. I remember telling users that short cuts used in some programs were getting them faster to the wrong answer. At the end, developing a very fast, double precision, multidimensional matrix inversion program was the solution, and using FORTRAN gave the most stable results. This HB approach is also able to deal with hysteresis.
The first and most challenging circuit analysis of a low noise amplifier, developed by Raytheon, was published14 for the first time, in cooperation with Robert Pucell of Raytheon and Tony Pavio of Texas Instruments. We demonstrated very accurate results using SPICE type data for GaAs FETs. They were hard to come by; we ended up using a modified Materka model.15-19 The actual circuit was published in Microwave Journal.20 So far, I have demonstrated that the noise analysis can be done solely using available and accurate SPICE parameters of GaAs FETs and its family members.
But the really needed large-signal circuit analysis was the oscillator. To implement the proper FET15-19 and BJT20-22 models and its derivatives was quite a task. The internal noise modeling was based on the noise correlation matrix2 and the results were published by W. Anzill, F. X. Kaertner and P. Russer in 1992.23 In 1987, the Microwave Harmonica program by Compact Software was proven to be reliable.20 The next step was to match the measured results of practical circuits. Hewlett Packard had the first, reliable phase noise system; Dieter Scherer was the lead engineer who educated us all. Today, the leading phase noise analyzer is the Rohde and Schwarz FSWP/8/26/50.
For a systematic approach, even without a simulator, it is useful to have large-signal S-parameters.2,24 The large-signal parameters of bipolar transistors, which had not been derived at the time of Kaertner’s work, are best obtained from measurements.24 The proper de-embedding procedure19 translates the external measurements to the actual chip (see Figure 1a), and a network analyzer with variable output power is needed for the measurement (see Figure 1b). With large-signal operation, the BJT behaves differently than for low noise applications,18-22 as shown in Figure 2.25
Kaertner Colpitts Oscillator
With this background, I would like to analyze the circuit used by Kaertner as the basis of his brilliant paper.8,23 The component values in the schematic of Figure 3a are taken from his publication: R1 = 350 Ω, R2 = 110 kΩ, RL = 500 Ω, L1 = 10 µH, L2 = 30 nH, C1 = 10 pF, C2 = 940 pF, C3 = 2.7 nF, C4 = 1.5 nF and T = BFR35A.
Kaertner made one simplification that in circuit theory is deadly: L2 was assumed to have infinite Q. For his approach, as the circuit will actually load the unloaded Q, this is permissible. With an infinite Q and with C2 = 940 pF, it will oscillate. Once a real Q, like QL =100, is used, the value of C2 must be reduced to 100 pF; then all works well. The feedback has to be increased, and it is advisable to reduce C4 to 100 pF, as it is not possible to make a capacitor without parasitic inductance. The same applies to the 10 µH inductor, which is probably resonant at the operating frequency; 1 µH seems to be a better choice. Kaertner published the calculated phase noise of his oscillator,4 pointing out correctly that the flicker contribution was not included.
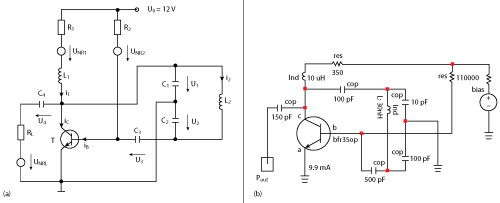
Figure 3 Colpitts oscillator analyzed by Kaertner (a) and circuit schematic in Compact Software (b).
Figure 3b shows Kaertner’s oscillator circuit when modeled with Compact Software Microwave Harmonia, to use the HB technique. The simulation includes the flicker noise exponent (AF) and the flicker noise constant (KF) and the simulation provides results tracking Kaertner’s publication (see Figure 4a). The influences of AF and KF are clearly seen at 1 kHz. The simulation also predicts the output power and harmonic content (see Figure 4b). The output power is approximately 16 dBm with about 20 dB harmonic suppression. This indicates a good operating Q of the resonant circuit. The analysis tracks the performance very well.
Figure 4 Simulated phase noise (a) and output power vs. frequency (b) of the Kaertner oscillator.
Summary
This brief history provides insight into the struggle to develop and validate a general purpose, nonlinear computer-aided design (CAD) tool that correctly predicts large-signal noise in amplifiers, frequency doublers and mixers. There are many more examples.2,14
There were many excellent contributors. Vittorio Rizzoli probably contributed the most, and my team’s effort to test and validate the Serenade Harmonica program should not be underestimated. Later, a CAD independent mathematical time domain calculation was developed, which, without immediately resorting to an expensive tool, can predict the noise performance of oscillators.2,23-24
Appendix
Although Leeson’s phase-noise model provides a valuable insight into the oscillator design from engineering perspectives, it cannot explain some of the important phase noise phenomena. This is due to some assumptions made about the linearity and time-invariant behavior of the system. When comparing the measured results of oscillators with the assumptions made in Leeson’s Equation, one frequently obtains a de facto noise figure in the vicinity of 20 to 30 dB and an operating Q that is different than the assumed loaded Q, therefore must be determined from measurement; diminishing the predictive power of the Leeson’s phase noise.
Leeson’s model observes the asymptotic behavior of phase-noise at close-to carrier offsets, asserting that phase-noise goes to infinity with 1/f3 rate. This is not correct as it implies an infinite output power for oscillator. For noisy oscillators it could also suggest that L(f) >0 dBc/Hz, this singularity arises from linearity assumption for oscillator operation around steady-state point. In fact, the linear model breaks down at close-to-carrier frequencies where the phase-noise power is strong.5 Considering a nonlinear model for the oscillator in absence of flicker noise, these singularities can be resolved by expressing the phase noise in the form of a Lorentzian function1,2,4
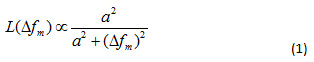
where a is a fitting parameter.
Although Equation (1) models the spectrum and avoids any singularity at Δfm=0 while maintaining the same asymptotic behavior as illustrated in Figure 1; this is an after-the-fact approach, not a predictive one. From Equation (1), the total power of phase-noise from minus infinity to plus infinity is 1, this means that phase-noise doesn’t change the total power of the oscillator; it merely broadens its spectral peak. Attempting to match the Leeson calculated curve “A” (Figure 1), the measured curve requires totally different values than those assumed due to up-conversion and down-conversion of noise components from harmonically related frequencies to around carrier frequency as depicted in Figure 2.5
References
- D. B. Leeson, “A Simple Model of Feedback Oscillator Noise Spectrum,” Proceedings of the IEEE, Vol. 54, No. 2, February 1966, pp. 329–330.
- U. L. Rohde, A. K. Poddar and G. Böck, The Design of Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, pp. 131–137.
- H. Hillbrand and P. Russer, “An Efficient Method for Computer Aided Noise Analysis of Linear Amplifier Networks,” IEEE Transactions on Circuits and Systems, Vol. 23, No. 4, April 1976.
- L. A. Hajimiri, “Linearity, Time Variation, and Oscillator Phase Noise,” RF and Microwave Oscillator Design, Artech House, 2002.
- A. Hajimiri and T. Lee, “A General Theory of Phase Noise in Electrical Oscillators,” IEEE Journal of Solid-State Circuits, Vol. 33, No. 2, February 1998, pp. 179–194.
- D. Ham and A. Hajimiri, “Concepts and Methods in Optimization of Integrated LC VCOs,” IEEE Journal of Solid-State Circuits, June 2001.
- D. Scherer, “Design Principles and Test Methods for Low Phase Noise RF and Microwave Sources,” RF and Microwave Measurement Symposium and Exhibition, Hewlett Packard, 1983.
- F. X. Kaertner, “Determination of the Correlation Spectrum of Oscillators with Low Noise,” IEEE Transactions on Microwave Theory and Techniques, Vol. 37, No. 1, January 1989.
- V. Rizzoli, F. Mastri and C. Cecchefti, “Computer-Aided Noise Analysis of MESFET and HEMT Mixers,” IEEE Transactions on Microwave Theory and Techniques, Vol. 37, September 1989, pp. 1401–1410.
- V. Rizzoli and A. Lippadni, “Computer-Aided Noise Analysis of Linear Multiport Networks of Arbitrary Topology,” IEEE Transactions on Microwave Theory and Techniques, Vol. 33, December 1985, pp. 1507–1512.
- V. Rizzoli, F. Mastri and D. Masotti, “General-Purpose Noise Analysis of Forced Nonlinear Microwave Circuits,” Military Microwave, 1992.
- R. J. Gilmore and M. B. Steer, “Nonlinear Circuit Analysis Using the Method of Harmonic Balance—A Review of the Art. Part I. Introductory Concepts,” International Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 1, No. 1, January 1991, pp. 22–37.
- R. J. Gilmore and M. B. Steer, “Nonlinear Circuit Analysis Using the Method of Harmonic Balance—A Review of the Art. Part II. Advanced Concepts,” International Journal of 367T.
- U. L. Rohde and D. P. Newkirk, “RF/Microwave Circuit Design for Wireless Application,” Wiley, 2000.
- R. A. Pucel, H. A. Haus and H. Statz, “Signal and Noise Properties of Gallium Arsenide Microwave Field-Effect Transistors,” Advances in Electronics and Electron Physics, Academic Press, Vol. 38, 1975.
- U. L. Rohde, “New Nonlinear Noise Model for MESFETs Including MM-Wave Application,” First International Workshop of the West German IEEE MTT/AP Joint Chapter on Integrated Nonlinear Microwave and Millimeterwave Circuits (INMMC’90) Digest, Duisburg University, October 3–5, 1990.
- U. L. Rohde, “Improved Noise Modeling of GaAs FETs: Using an Enhanced Equivalent Circuit Technique,” Microwave Journal, November 1991, pp. 87–101; December 1991, pp. 87–95.
- M. Rudolph, R. Doerner, K. Beilenhoff and P. Heymann, “Scalable GaIn/GaAs HBT Large-Signal Model,” IEEE Transactions on Microwave Theory and Techniques, Vol. 48, December 1990, pp. 2370–2376.
- R. A. Pucel, W. Struble, R. Hallgren, and U. L. Rohde, “A General Noise De-embedding Procedure for Packaged Two-Port Linear Active Devices,” IEEE Transactions on Microwave Theory and Techniques, Vol. 40, No. 11, November 1992, pp. 2013–2024.
- U. L. Rohde, A. M. Pavio and R. A. Pucel, “Accurate Noise Simulation of Microwave Amplifiers Using CAD,” Microwave Journal, Vol. 31, No. 12, December 1988, pp. 130-141.
- R. A. Pucel and U. L. Rohde, “An Exact Expression for the Noise Resistance Rn of a Bipolar Transistor for Use with the Hawkins Noise Model,” IEEE Microwave and Guided Wave Letters, Vol. 3, No. 2, February 1993, pp. 35–37.
- C. C. McAndrew, J. A. Seitchik, D. F. Bowers, M. Dunn, M. Foisy, I. Getreu, M. McSwain, S. Moinian, J. Parker, D. J. Roulston, M. Schroeter, P. van Wijnen and L. F. Wagner, “VBIC95, The Vertical Bipolar Inter-Company Model,” IEEE Journal of Solid-State Circuits, Vol. 31, No. 10, October 1996, pp. 1476–1483.
- W. Anzill, F. X. Kaertner and P. Russer, “Simulation of the Single-Sideband Phase Noise of Oscillators,” Second International Workshop of Integrated Nonlinear Microwave and Millimeterwave Circuits, 1992.
- U. L. Rohde and A. Apte, “Everything You Always Wanted to Know about Colpitts Oscillators,” IEEE Microwave Magazine, Vol. 17, No. 8, August 2016, pp. 59–76.
- U. L. Rohde, “Parameter Extraction for Large Signal Noise Models and Simulation of Noise in Large Signal Circuits Like Mixers and Oscillators,” 23rd European Microwave Conference, Madrid, September 6–9, 1993.
