Figure 1 Simplified block diagram of a T/R front-end in a phased array.
High data rate wireless communication systems require high spectral efficiency, power efficiency and low levels of signal distortion. At issue is that low levels of signal distortion are obtained with substantial signal back-off from the saturation region. As the amount of signal back-off increases, the nonlinear distortion decreases at the expense of power efficiency. Error vector magnitude (EVM) is a common figure of merit used to evaluate the quality of a transmitted signal as it relates to the overall signal-to-noise plus interference ratio (SNIR).1 Quantifying EVM during the RFIC design flow is becoming increasingly important, particularly in high-order modulation transmission systems.2 That is because integration of EVM analysis during the RFIC design and optimization phases is essential to producing a system with optimum EVM performance over a wide range of output power.
Problem Predicting EVM
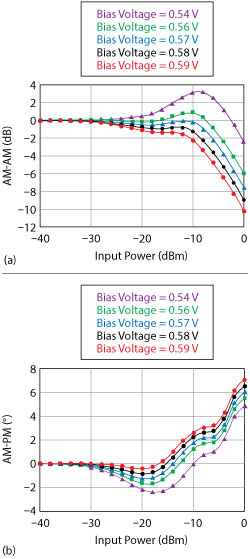
Figure 2 Simulated AM-AM (a) and AM-PM (b) distortion of the core IC.
The traditional RFIC design flow uses continuous wave (CW) stimulus to evaluate signal integrity, nonlinear terms such as third-order intermodulation products and nonlinear compression points of the subsystem. While CW stimulus provides fast insight into the system’s performance, it offers a limited understanding of the impact of nonlinear distortion on modulation accuracy. The use of modulating signals in the RFIC design flow offers an alternative. However, this approach is not widely used due to the long simulation times when a transistor-level design with strong nonlinear characteristics is subject to higher-order modulation. The complexity of the simulation environment also presents a challenge. EVM evaluation is normally performed only after the completion of the design, rather than during the RFIC design flow. By not properly taking EVM analysis into account during the design phase—optimizing circuits to a minimum EVM over a wide range of input power levels and multiple circuit conditions—sub-optimum IC performance in terms of EVM can result.
The traditional expression for the third-order intercept point of a cascaded series of components results in poor prediction of the EVM across a wide range of input power levels:
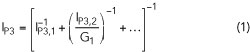
where G1 is the gain of the first stage and the IP3,i represents the third-order intercept point of the ith-stage.
Consider the simplified block diagram in Figure 1 of a transmitter/receiver (T/R) front-end in a phased array. The nonlinear elements are the power amplifier (PA) and core IC. The latter is responsible for the phase and amplitude control to obtain specific beamforming characteristics. Rather than the third-order intercept points, the nonlinear behavior of the core IC and PA are described by the AM-AM and AM-PM functions. These functions provide a more accurate description of the nonlinear characteristics of the system. By defining the simple subsystem of Figure 1 in terms of AM-AM and AM-PM distortion, and considering that the quiescent points of the core IC and PA stages vary according to the output power level, RF subsystem design for optimum EVM becomes very challenging, in part because multiple combinations of power levels and quiescent currents between the core IC and PA may lead to similar saturation power levels, yet very different EVM performance.
Many modern wireless communication systems employ orthogonal frequency-division multiplexing (OFDM) with 64-QAM or higher modulation and bandwidths of 40 MHz or greater. EVM of 1.8 percent and below is normally required, and this demands careful system optimization. Translating stringent EVM requirements into an actual RFIC design flow is of paramount importance to deliver a system with high-power efficiency and excellent EVM performance.
Distortion and EVM
To better understand the AM-AM and AM-PM nonlinear characteristics and their relationship to EVM, refer to Figure 1. The bidirectional T/R front-end comprises a vector modulated phase shifter, a low noise amplifier, a PA and a bidirectional transfer switch. Amplitude control is obtained by varying the gain at the different amplification units of the core IC. A common approach to implementing variable gain amplification at RF frequencies is to change the bias and, therefore, the quiescent current of the device. By varying the quiescent current, the device’s transconductance changes and so, too, does the voltage gain. In addition to the amplitude control, the nonlinear characteristics of the core IC also vary with the quiescent current. Figure 2 shows the simulated AM-AM and AM-PM distortions of the 180 nm CMOS core IC versus input power and bias. Inspection of these curves does not provide clear insight into the optimum operating point for EVM over a wide range of input power levels and modulation formats.
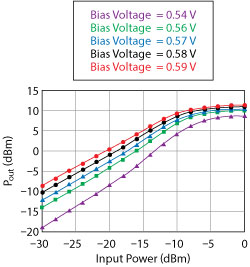
Figure 3 Output vs. input power of the core IC.
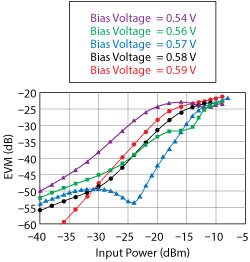
Figure 4 Simulated EVM of the core IC vs. bias.
The traditional output versus input power characterization, shown in Figure 3, offers even less information about the EVM at different input power levels. A common practice is to roughly estimate the amount of power back-off from the 1 dB compression point to define the maximum linear output power. For example, one could use the curves of Figure 3 and choose 13 dB back-off, which defines an approximate linear input power of ‐22 dBm for 256-QAM OFDM. Approximately 12 dB gain control is obtained by varying the bias point from 0.54 to 0.59 V.
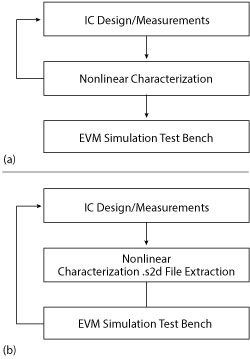
Figure 5 Traditional design flow (a) and modified flow that integrates EVM analysis (b).
The simulated EVM of the core IC with 256-QAM and a 40 MHz bandwidth is shown in Figure 4, using the same bias conditions shown in Figures 2 and 3. As the bias voltage approaches the 0.54 V threshold voltage, EVM versus input power degrades and the voltage gain decreases rapidly (see Figure 3). Figure 4 shows how the operating condition affects EVM. At very high input power level, where the core IC operates in compression, the bias point has little impact on EVM. As the input power decreases, lower EVM is obtained with a bias voltage of 0.57 V. For input power levels below ‐32 dBm, the high bias voltages (0.58 and 0.59 V) provide lower EVM. One conclusion is that determining EVM is almost impossible by merely inspecting the nonlinear characteristics of the IC derived from CW excitation. A thorough EVM analysis, as an integral part of the RFIC design flow, is required to optimize circuit conditions for minimum EVM. Also, subsystem implementations of the T/R front-end in Figure 1 and spatial filters with adjustable weighing functions demand that integrated EVM simulations be part of the RF system design flow.
EVM In the Design Flow
The previous section described the importance of integrating EVM analysis in the RFIC design flow for higher-order modulations, i.e., 64-QAM and higher, where EVM levels below ‐30 dB are required. Figure 5 illustrates two RFIC design flows that can be used for EVM analysis. Figure 5a shows the traditional EVM simulation flow. Here, the verification methodology for RFIC design, which includes process-voltage and temperature (PVT) variation analysis at the circuit level, layout verification, functional verification and EVM verification at the system level, is carried out at the end of the design. Performing EVM analysis only in the verification stage, without taking it into account during the design phase, leads to suboptimal design and slows the overall design process. The latter occurs when the circuit must be redesigned because the device’s quiescent point has to change to meet EVM performance, which occurs particularly in cases where stringent EVM specifications are demanded.
Introducing EVM simulations during the RFIC design flow creates a few difficulties. That is because EVM simulations are slow compared to simulations based on CW stimulus, and the design environment is different than the normal RFIC design environment. A complete transistor-level circuit description for EVM analysis is very time consuming and, ultimately, too complex for EVM analysis. The RFIC design flow in Figure 5b offers a way to overcome these limitations: the nonlinear AM-AM and AM-PM characteristics at various bias conditions are inserted automatically, with additional small-signal and noise parameters, into the GCOMP7 option of the .s2d file format. The resultant .s2d file defines the behavior of a nonlinear amplifier used for EVM simulation.
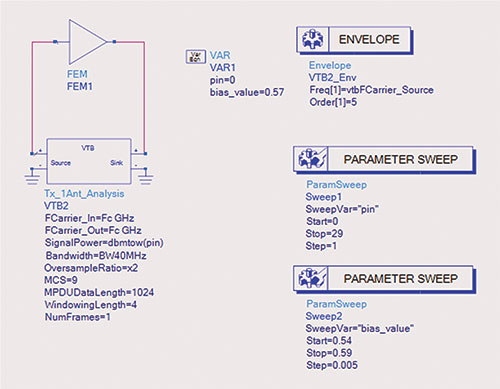
Figure 6 EVM simulation test bench using Keysight’s ADS software.
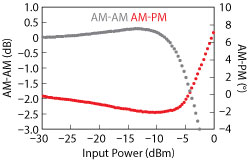
Figure 7 Measured AM-AM and AM-PM distortion of the DUT.
Figure 6 shows the test bench used for the evaluation of the implemented EVM using Keysight’s Advanced Design System (ADS). For the EVM analysis, a 256-QAM, 40 MHz bandwidth signal was used. The input power level and bias voltage were parametrized, comprising 33 power levels simulated over 11 bias conditions, resulting in 363 different conditions for simulation. The EVM simulation based on the .s2d files consumed just a fraction of time compared to the simulation based on the transistor-level design. The latter becomes impractical to analyze in the design flow of Figure 6b due to the complexity of the circuit and the long simulation times required. The same circuit, modeled with .s2d format files, required only a few seconds to analyze the EVM—a substantial reduction in the EVM simulation time that enabled the practical integration of EVM analysis into the RFIC design flow.
Simulated and Measured Results
Using a circuit representation based on the .s2d file format and the test bench shown in Figure 6, EVM simulations were carried out to compare with the measured EVM. A 256-QAM, 40 MHz bandwidth modulating signal was used for the simulations. The measurements of AM-AM and AM-PM distortion were initially performed using spectrum and network analyzers, prior to EVM evaluation. Figure 7 shows the measurement results of the nonlinear characterization of the device under test (DUT). A .s2d file format was created to describe the small- and large-signal characteristics of the DUT. The GCOMP7 option was used to model the nonlinear behavior.

Figure 8 EVM measured using the Keysight E4438C vector signal generator and N9020A signal analyzer.
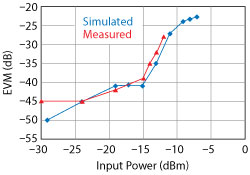
Figure 9 Simulated vs. measured EVM.
Figure 8 shows the setup for EVM measurement. Power calibration was performed to determine the input power levels during nonlinear characterization of the DUT and EVM measurements. To assure the accuracy of the input power for EVM readings, the output power of the vector signal generator remained constant, while the different input power levels applied to the DUT were varied using an external variable attenuator. Cable losses were extracted and de-embedded from the measurement results.
Both the measurement and simulation of EVM are shown in Figure 9. Excellent agreement was obtained between simulation and measurement at moderate and high input power. At power levels below −25 dBm, the sensitivity of the measurement equipment limits the ability to measure EVM below −45 dB. The results show the importance of evaluating EVM, particularly at moderate power levels, where the results are highly dependent on the amplitude and phase distortion characteristics of the nonlinear circuit.
Conclusion
The importance of integrating EVM analysis into the RFIC design flow, particularly for systems with EVM specifications below ‐30 dB, cannot be overstated. Without including EVM in the design flow, the complete RF subsystem can have suboptimal EVM under different input power and bias conditions. Small changes in the bias of an output stage can result in very different EVM over a wide range of input power. Fortunately, a substantial reduction in the simulation time for EVM evaluation can be obtained through AM-AM and AM-PM characterization and by incorporating this into the .s2d file format. Using this methodology for integrating EVM evaluation into the design flow, engineers can simulate EVM that is in excellent agreement with measured EVM—and in a fraction of the time.n
Acknowledgment
The authors would like to thank K. Manin, I. Levie, P. Steinberg and E. Turgerman for fruitful discussions and measurement support.
References
- R. Hassung et al., “Effective Evaluation of Link Quality Using Error Vector Magnitude Techniques,” Wireless Communication Conference, pp. 89–94, 1997.
- P. Naraine, “Predicting the EVM Performance of WLAN Power Amplifiers with OFDM Signals,” Microwave Journal, May 2004.

