In microwave engineering we are accustomed to thinking of the electromagnetic energy in our circuits as transmitted by waves. Now, new technologies are being developed that deal with signals at the level of single photons where this is no longer valid. Here we describe some of the challenges and opportunities in this rapidly developing field.
While Maxwell’s equations are valid at all frequencies, in practice, we still think of the electromagnetic spectrum as being “segmented” because of the vastly different tools used to manipulate, for example, laser light versus microwaves. In this review we consider microwave “single photons,” which are single energy quanta of radiation, with four to five orders of magnitude lower energy than their optical counterparts. A 1 GHz photon has an energy of 0.66 yoctojoule (0.66 *10-24J); 1/200,000th the energy of an optical photon at 1.55 µm or, equivalently, about 1/6000th the thermal energy at room temperature. This explains why, until recently, single photon sources were available only for optical frequencies. As discussed below, manipulating the particle nature of microwave signals is extremely challenging but offers exciting scientific and technological prospects.
Over the past couple of decades, enormous progress has been made in the research field now known as solid-state quantum engineering. The origin of this field can be traced back to the mid-eighties, when the scientific community started to wonder if it would be possible to observe exotic quantum effects such as entanglement and superposition in man-made electronic circuits.1 The invention of quantum computing algorithms, promising to solve hard computational problems, led to an explosion of experimental activity in the field. However, it was not until the late nineties, with the creation of the first solid-state quantum bits (qubits) that the field really took off.2 The past few years have seen the complexity of these quantum circuits go up enormously; some circuits now contain hundreds of elements3 all operating at microwave frequencies, typically in the range 1 to 12 GHz.
The headline-grabbing long-term goal of all of this effort is to build a quantum computer; a type of a computing device that uses quantum algorithms to solve certain problems, most notably factoring large integers for code breaking, much faster than a classical computer. However, in the pursuit of this goal researchers have also developed a toolbox containing novel microwave components and devices that may turn out to be useful in a much wider range of applications.
This is a very active research field and there are many ongoing projects around the world. The authors are involved in one such international project called MICROPHOTON which is funded by Euromet.4 In this brief review, we will describe some of the latest developments in this rapidly advancing area.

Figure 1 The sample stages of a dilution refrigerator equipped with microwave lines, where the different levels get progressively colder. The device under test is mounted at the bottom, where T ≈ 10 mK.
QUANTUM CIRCUITRY
One remarkable aspect of Maxwell’s equations is that they are valid even in the “quantum” regime where we are dealing with single photons. This means that single microwave photon systems can, from an engineer’s point of view, be treated as any other microwave circuits and we can use many of the same familiar tools. The systems need detectors, sources and ways to manipulate and guide the photons.
It would be difficult to distinguish a chip with a quantum circuit from one with a conventional electronic circuit. A typical chip made using, for example, superconducting device technology (one of the leading contenders in this field) contains 50 Ω transmission lines (usually coplanar waveguides), planar inductors (spirals or meanderlines) and capacitors (interdigital, planar or parallel-plate types) fabricated on a low loss substrate (usually sapphire or silicon). Other common elements include resonators, either lumped or transmission line λ/2 and λ/4 sections.
The key elements of quantum circuits are qubits that are used as “artificial atoms.” For superconducting circuitry these are typically based on so-called Josephson junctions; although they are also fabricated using standard microfabrication techniques and are therefore, from a design point of view, just another type of circuit element. As the complexity of these circuits continues to grow, so does the importance of precision microwave engineering.
A COOL TECHNOLOGY
The energy of a single microwave photon is very small compared to the thermal background at room temperature. This dictates that any device using single microwave photons must be cooled to cryogenic temperatures. In practice, most of the single photon devices that are currently being developed must be operated at temperatures below 0.1 K.5-8 Not long ago this would have meant using cryostats that used liquid helium for cooling, which is generally unsuitable for use outside of research labs; however, rapid progress in the field of cryogenics has already seen the development of much more user-friendly dry (cryogen free) mechanical systems (see Figure 1) that require only a source of electricity to run.9 Currently available systems are still too bulky and expensive for widespread use, but smaller and cheaper systems are in development.
At these low operating temperatures, superconductors are typically used for transmission lines even when normal metals such as copper would, in principle, work. The benefit is very low loss; the equivalent resistance can be lower than 10-4Ω/square at GHz frequencies. Hence, it makes sense to fabricate most circuit elements out of superconducting aluminum or niobium, for example, rather than copper even though this is not, strictly speaking, necessary from a functional point of view. This also means that circuit elements can usually be modeled as lossless metals.
DETECTING SINGLE MICROWAVE PHOTONS
Detecting a single microwave photon is extremely challenging. Several companies now produce low noise amplifiers (LNA) with noise temperatures as low as 2.1 K for C-Band (4 to 8 GHz);10however, even this impressively low figure is still too high to detect a single microwave photon. Moreover, there are intrinsic issues, such as amplifier self-heating, based on conventional III-V semiconductors making it unlikely that they will ever be useful as practical single photon detectors. In order to overcome this problem, new types of advanced instrumentation, parametric amplifiers (paramps) and bifurcation amplifiers, have been developed over the past few years.
Parametric amplification is not a new idea, but paramps based on superconducting circuits have literally pushed the technology to its physical limits. Several research groups have demonstrated designs that are truly quantum limited; i.e., noise is limited only by quantum fluctuations.11 Typical gain of these amplifiers is 20 to 30 dB, which brings the signal up to a level where conventional LNAs can be used for further amplification.

Figure 2 Scanning electron microscopy of a photon detector based on conversion of a single photon into charge. The device is fabricated by MICROPHOTON partner PTB (Germany).6
For single photon detection, it would be desirable to develop a circuit that sends out, for example, a voltage pulse (a click) whenever a single photon is absorbed. These click detectors are widely available for frequencies in the optical range, where typical photon energies are 1,000,000 times higher, but has proven very difficult to develop for microwave frequencies. However, recent results from several research groups, suggest that such detectors might soon become available.8
An approach, which has already demonstrated single photon sensitivity in special circumstances, utilizes phenomena that directly exploit the quantum-particle nature of photons. Photons are trapped in a resonator (the microwave equivalent of photons bouncing between two mirrors) and their presence detected indirectly using a qubit.5This method is extremely sensitive, but in the absence of additional circuitry, is inherently slow and inefficient.
Figure 2 shows an example of a threshold detector that sends out an electrical signal when a single photon with high enough energy is absorbed. The implementation in Figure 2 is a nanofabricated circuit which detects absorbed photons by sensing when electrons are knocked out of a charge trap using a single electron transistor (essentially a very sensitive electrometer). Absorption events of single microwave photons can be detected clearly, but the quantum efficiency of such a detector is very low; only a tiny fraction of incoming photons are actually absorbed in the detector.
A very sensitive thermal power sensor can also, at least in principle, be used for sensing microwave photons. This would detect a single photon bolometrically or calorimetrically by measuring the increase in temperature as the photon hits a 50 Ω absorber terminating a waveguide. A recently demonstrated state-of-the-art result for this approach is a detector capable of sensing pulses containing about 200 photons at 8.4 GHz.12 Other approaches include using so-called bifurcation amplifiers (essentially bistable threshold amplifiers) that can already be made sensitive enough to detect pulses containing a few photons.13 Unfortunately, both thermal and bifurcation amplifier detectors realized to date must integrate the signal for a long time to achieve anywhere near single photon sensitivity, meaning this is an area with a lot of potential for improvement.
An efficient single microwave photon detector would be useful not only as a fundamental physics experiment or for quantum information processing. In principle, it would also enable counting the number of incoming photons per second, thus providing a measure of absolute microwave power without any need for calibration.
GENERATING MICROWAVE PHOTONS
Creating an electric circuit that functions as an on-demand source of microwave photons has only become possible in the past decade. The seemingly obvious way to do this would be to take an ordinary microwave generator and attenuate its output; however, this approach does not work. While it can create a source that over some timespan, on average, emits energy equivalent to one photon (or even less) it cannot be used to make a true single photon source, since the photons are uncorrelated. In a true single photon source, the spacing between photons is very regular, which is what gives the radiation its non-classical nature.
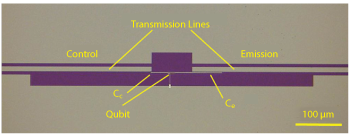
Figure 3 Single photon source based on a superconducting qubit (an “artificial atom”). The qubit is asymmetrically coupled to two 50 Ω coplanar waveguides via coupling capacitances Cc = 0.5 fF and Ce = 5 fF.
So how do you generate a single photon? The solution is once again to use quantum technology originally developed for quantum computing. The quantum bit, or qubit, is the quantum mechanical version of the digital bit, albeit with some very special properties. This can be exploited to make a single photon source since a qubit switching from its “1” state to “0” emits a single photon. It is similar to how an atom emits light when an electron moves from an excited state to a lower energy state. The engineering challenge is to create circuits that can reliably prepare a qubit in its “1” state and also guide the resulting photon. Doing this at optical frequencies is extremely difficult due to the low collection efficiency of emitted photons in three dimensional space. In the microwave regime, however, where transmission lines are one dimensional and circuit elements are “point-like” with respect to a wavelength of radiation, quantum output efficiencies are already above 50 percent in the first candidate devices. Work on devices for single photon generation in the microwave regime was pioneered by research groups at Yale University in the U.S. and ETH in Switzerland.7,14
An implementation of a microwave single photon source is shown in Figure 3. This circuit is based on a qubit embedded in a 50 Ω coplanar waveguide. The trick here is that the qubit is much more strongly coupled to the “out” port than the “in” port. A large amplitude trigger pulse generated by a conventional microwave pulse generator in the “in” port excites the qubit, which then (a few tens of nanoseconds later) decays into the “out” port, emitting a photon. The coupling capacitances are chosen in such a way that stray coupling between ports is minimized. Hence, this circuit functions a bit like the quantum equivalent of a monostable multivibrator (a familiar circuit from conventional electronics) in that it is an on-demand source. MICROPHOTON partners RHUL and NPL (U.K.) have with Japanese collaborators recently demonstrated on-demand generation of single microwave photons with such a source.15
There has been remarkable progress in this area over the past few years, but making large-scale quantum circuits still presents numerous challenges.16 Fortunately, where hundreds or thousands of qubits are needed to build a practical quantum computer, only one is required to make a source. Hence, practical single microwave photon sources are likely to become available for real-world applications much sooner than quantum computers.
CONTROLLING PHOTONS
Emitting and detecting single microwave photons remains challenging and is much more difficult than in the optical regime. However, microwave photons have one very important advantage over optical photons: they are much easier to control. A signal consisting of a stream of individual microwave photons will behave just like any other microwave signal, and normal passive microwave components can therefore be used.
Researchers in the field have developed specialized circuits (often using Josephson junctions or qubits as building blocks), but these are typically, from an engineering point of view, little more than high performing versions of commonly used elements such as filters, couplers, transformers and switches. The main difference between these and off-the-shelf microwave components is usually only that they have very low losses and can be operated at low temperatures.
There are some philosophical differences, however, in how one chooses to interpret what is happening. An example is the common hybrid coupler which is functionally identical to the half-silvered mirror commonly used in optics. The magnitude of a classical signal will be split equally between the two output ports; but, if the signal consists of a single photon, it can only exit through one of the ports. This is the one example of a phenomenon one would never encounter in a classical circuit.
APPLICATIONS
The technology discussed in this article was developed primarily for fundamental research and designed to meet the needs of researchers working in the field of solid-state quantum engineering. While widespread usage of quantum computers is still decades away, an obvious question is whether there are any current real-world applications of single microwave photon technology. As with any new technology, it is difficult to predict the impact. The first users will likely be scientists working in radio astronomy and other areas where the extra overhead in terms of cost and equipment can be tolerated if it leads to significantly higher performance. The paramp, essentially just a very good microwave amplifier, is likely to find applications in demanding areas such as space communications.
Another area that will benefit from this technology is precision metrology. The quantum nature of this technology is an advantage since it gives direct connection to the primary standards of the international system of units; this would be especially true if sources and detectors become available with efficiencies high enough to allow for direct microwave photon detection.
CONCLUSION
Microwave photonics is a new field and contains elements that one would not normally encounter in microwave engineering. However, most of the fundamentals are still the same as for any other microwave circuit design; and, as the complexity of quantum circuitry continues to grow, so does the importance of sound microwave engineering.n
References
- R. P. Feynman, “Simulating Physics with Computers,” International Journal of Theoretical Physics, Vol. 21, No. 6/7, 1982, pp. 467–488.
- Y. Nakamura, Yu. A. Pashkin and J. S. Tsai, “Coherent Control of Macroscopic Quantum States in a Single-Cooper-pair Box,” Nature, Vol. 398, April 1999, pp. 786–788.
- D-Wave 2000Q Technology Overview, www.dwavesys.com.
- A. J. Manninen, A. Kemppinen, E. Enrico, M. Kataoka, T. Lindström, A.B. Zorin, S.V. Lotkhov, M. Khabipov, M. Möttönen, R.E. Lake, J. Govenius, J.P. Pekola, Yu.A. Pashkin, P.J. Meeson and O.V. Astafiev, “Measurement and Control of Single-Photon Microwave Radiation on Chip,” IEEE Conference on Precision Electromagnetic Measurements, August 2014.
- B. R. Johnson, M. D. Reed, A. A. Houck, D. I. Schuster, Lev S. Bishop, E. Ginossar, J. M. Gambetta, L. DiCarlo, L. Frunzio, S. M. Girvin and R. J. Schoelkopf, “Quantum Non-Demolition Detection of Single Microwave Photons in a Circuit,” Nature Physics, Vol. 6, June 2010, pp. 663–667.
- S. V. Lotkhov, B. Jalali-Jafari and A. B. Zorin, “Photon-Activated Electron Hopping in a Single-Electron Trap Enhanced by Josephson Radiation,” Applied Physics Letters, Vol. 108, No. 172603, April 2016.
- A. A. Houck, D. I. Schuster, J. M. Gambetta, J. A. Schreier, B. R. Johnson, J. M. Chow, L. Frunzio, J. Majer, M. H. Devoret, S. M. Girvin and R. J. Schoelkopf, “Generating Single Microwave Photons in a Circuit,” Nature, Vol. 449, September 2007, pp. 328–331.
- K. Inomata, Z. Lin, K. Koshino, W. D. Oliver, J. S. Tsai, T. Yamamoto and Y. Nakamura, “Single Microwave-Photon Detector Using an Artificial [Lambda]-Type Three-Level System,” Nature Communications, Vol. 7, No. 12303, July 2016.
- R. Radebaugh, “Cryocoolers: the State of the Art and Recent Developments,” Journal of Physics: Condensed Matter, Vol. 21, No. 16, March 2009. See also www.oxinst.com or www.bluefors.com.
- www.lownoisefactory.com/ or www.cosmicmicrowavetechnology.com/.
- M. Devoret and A. Roy, “Introduction to Quantum-limited Parametric Amplification of Quantum Signals with Josephson Circuits,” arXiv:1605.00539 [cond-mat.mes-hall], May 2016.
- J. Govenius, R. E. Lake, K. Y. Tan and M. Möttönen, “Detection of Zeptojoule Microwave Pulses Using Electrothermal Feedback in Proximity-Induced Josephson Junctions,” Physical Review Letters, Vol. 117, No. 3, July 2016, pp. 030802-1-6.
- R. Vijay, M. H. Devoret and I. Siddiqi, “Invited Review article: The Josephson Bifurcation Amplifier,” Review of Scientific Instruments, Vol. 80, No. 11, November 2009.
- D. Bozyigit, C. Lang, L. Steffen, J. M. Fink, C. Eichler, M. Baur, R. Bianchetti, P. J. Leek, S. Filipp, M. P. da Silva, A. Blais and A. Wallraff, “Antibunching of Microwave-Frequency Photons Observed in Correlation Measurements Using Linear Detectors,” Nature Physics, Vol. 7, No. 2, February 2011, pp. 154–158.
- Z. H. Peng, S. E. de Graaf, J. S. Tsai and O. V. Astafiev, “Tuneable On-Demand Single-Photon Source in the Microwave Range,” Nature Communications, Vol. 7, No. 12588, August 2016.
- M. Mohseni, P. Read, H. Neven, S. Boixo, V. Denchev, R. Babbush, A. Fowler, V. Smelyanskiy and J. Martinis, “Commercialize Quantum Technologies in Five Years,” Nature, Vol. 543, No. 7644, March 2017, pp. 171–174.
Tobias Lindström is a senior research scientist in the Department for Quantum Science at the National Physical Laboratory in the U.K. His research interests include superconducting resonators and circuits as well as high coherence materials for solid-state quantum technology.
Russell Lake is currently employed as a physicist at the National Institute of Standards and Technology in Boulder, Colorado (USA) in the Quantum Electromagnetics Division. His research interests include quantum microwave circuits and materials physics.
Yuri Pashkin is a professor at the Physics Department at Lancaster University. Prior to joining Lancaster in 2011, he was a principal researcher at the research laboratory of NEC Corporation in Tsukuba (Japan). His research interests include physics of superconducting and Coulomb blockade devices, quantum metrology and quantum computing and quantum sensing.
Antti Manninen is a senior principal scientist in VTT Technical Research Centre of Finland Ltd., Centre for Metrology MIKES. His research interests include metrological applications of quantum phenomena (Josephson effect, quantum Hall effect and single charge transport) and microelectromechanical devices.
