A compact wideband quadrature hybrid coupler (QHC) with an arbitrary power division ratio is based on an artificial lumped-element simplified composite right-/left-handed transmission line (SCRLH TL) structure. The SCRLH TL can be easily tailored to satisfy the high or low impedance condition necessary to produce a QHC with a high power splitting ratio. An odd-even mode admittance resonant frequency ratio (n) is introduced to analytically formulate all the SCRLH TL elements, developing a relationship between the n value and the SCRLH TL phase and impedance bandwidths. This establishes a simple criteria to expand the QHC bandwidth. A prototype proof-of-principle 900 MHz QHC with a 10 dB power division ratio is only 4.5 × 4.5 mm2 in size with greater than 32 percent bandwidth.
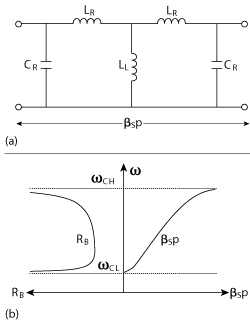
Figure 1 Circuit model of SCRLH TL unit cell (a) phase shift per unit cell to the right of the vertical axis and the real part of the Bloch impedance to the left of the axis (b).
Quadrature hybrid couplers (QHC) are widely used in modern microwave integrated circuits and antenna feed systems, providing equal or unequal power division with 90° phase difference between the main and coupled ports. In this paper, a wideband QHC with a greatly reduced footprint and high power division ratio is introduced. It features a simplified composite right-/left-handed (SCRLH) transmission line (TL) structure, a version of the CRLH TL that omits either the series capacitance or the shunt inductance in the unit cell, exhibiting a right-handed passband with nonlinear dispersion properties and a smooth Bloch impedance distribution.1 It has been employed in the design of dualband QHCs,2,3 where each QHC branch contains two unit cells. Each branch of the QHC described in this article consists of only one unit cell composed of lumped elements, resulting in a significant size reduction.
Nonresonant and resonant type CRLH TL structures have been used to design QHCs with wide bandwidth and improved phase balance,4,5 but their matching bandwidths improve little and can be even worse than those of their conventional counterparts. This is because the nonresonant type CRLH TL must satisfy the balanced state condition, i.e., seamless impedance transition from the left-handed passband to the right-handed passband; while for the resonant type CRLH TL, the impedance slope at the nominal frequency should be kept as small as possible. These are conditions not easily implemented in practice.
The SCRLH TL not only has controllable dispersion properties, but also has an intrinsic impedance distribution close to that of the balanced CRLH TL,6 ensuring that the QHC’s phase and impedance bandwidths are improved to the same degree. Chi7 demonstrated a rat-race coupler with 6 dB power splitting ratio using an unbalanced CRLH TL; but it is only a narrowband device, and if a higher power division ratio is required, it may no longer be feasible. In fact, a high power division ratio demands extremely high and low branch impedances simultaneously. This is a stringent constraint for the unbalanced CRLH TL as well as for a conventional TL, but can be easily satisfied by the SCRLH TL with a wide-ranging Bloch impedance.
There is an additional degree of freedom in the SCRLH TL after realizing the required phase and impedance conditions. The odd-even mode admittance resonant frequency ratio n is a key parameter by which all the SCRLH TL unit cell parameters can be defined. By selecting a rational n, the branch phase balance bandwidth can be widened to its best value with obtainable discrete lumped elements, while the branch impedance bandwidth is naturally guaranteed due to the smoothly distributed Bloch impedance.
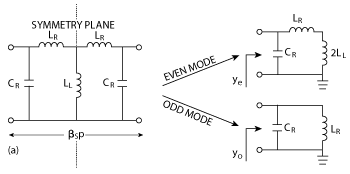
Figure 2 Odd-even mode equivalent circuits for the SCRLH TL unit cell.
SCRLH TL Analysis
The lumped circuit model of a single SCRLH TL unit cell is shown in Figure 1a, where LR is the series inductor, LL the shunt inductor, CR the shunt capacitor, βS the propagation constant and p the physical length. By virtue of the Bloch-Floquet theory, the phase shift βSp and the Bloch impedance ZB can be expressed as8

where A and B are the first and second elements of the unit cell transfer function matrix.6
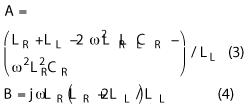
Typical frequency dispersion and Bloch impedance are shown in Figure 1b. The passband of the SCRLH TL is delimited by the zeroth-order resonant frequency ωcL and the Bragg frequency ωcH, over which the phase shift is nonlinear; while the Bloch impedance follows a continuous and smooth distribution with a large rise near both band edges. The odd-even mode method is used to determine the symmetrical SCRLH TL unit cell’s parameters. Corresponding odd-even mode equivalent circuits are shown in Figure 2, in which the odd-even mode input admittances are

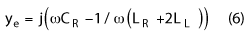
respectively, and their resonant frequency ratio is defined by

If the SCRLH TL unit cell is to be equivalent to a 90° uniform TL with characteristic impedance Z, the following equations should be satisfied at the working frequency ω09
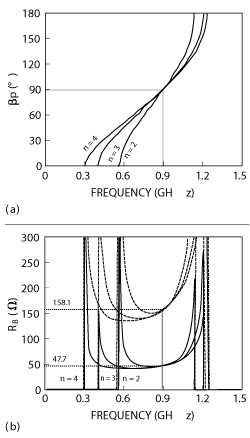
Figure 3 Frequency responses of dispersion (a) and Bloch impedance (b) for the SCRLH TL with different n (Zm branch: solid line, Zb branch: dash line).
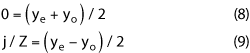
Substituting equations 5-7 into equations 8 and 9, we obtain

All lumped elements in the SCRLH TL unit cell are uniquely determined by n, once ω0 and Z are fixed. To study the effects of n on coupler bandwidth, equations 10-12 are substituted into equations 3 and 4, yielding
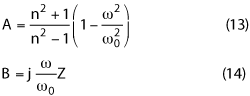
Equations 1 and 13 show that the dispersion frequency response of the SCRLH TL depends only on n; therefore, if an identical n value is chosen to design the QHC main-line and branch-line stubs, they will have fully consistent dispersive curves, which is beneficial in enlarging the coupler phase balance bandwidth.4 With equations 1, 2, 13 and 14, the SCRLH TL phase shift and impedance slopes at ω0 can be determined as
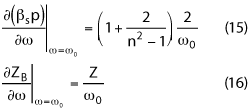
Figure 4 Lumped SCRLH TL based QHC; Circuit topology (a), fabricated prototype (b).
Equation 15 indicates that the dispersion curve slope at ω0 will decrease as n goes up, and it has a minimum value of 2/ω0. Equation 16 shows that the Bloch impedance slope at ω0 is independent of n but is proportional to Z. In fact, a broadband QHC can only be realized by simultaneously extending the phase shift and impedance bandwidths for all its branches.4 To increase the phase shift bandwidth, n should be as large as possible, however, since the dispersive curve slope has a minimal value and practically obtainable lumped elements are in discrete values, the same n should be applied to design both the main-line and branch-line stubs using equations 10 to 12 and 15. Additionally, the high impedance condition required to attain a high power division ratio will limit to a certain degree the QHC matching bandwidth according to equation 16.
LUMPED-ELEMENT SCRLH TL BASED QHC
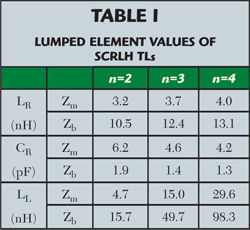
Let Δ= |S21|2 / |S31|2 be the power division ratio of the designed QHC. If Δ= dB, the characteristic impedances of the main-line and branch-line stubs are Zm = 47.7 Ω and Zb = 158.1 Ω,respectively.9 Table 1 lists the SCRLH TL element values with different n when f0 = 0.9 GHz, and the corresponding dispersion and impedance frequency responses are depicted in Figure 3. According to equation 7, n can be any value larger than one, but herein only n = 2, 3, 4 are considered for illustration. Figure 3a shows that although Zm ≠ Zb, the Zm and Zb branches, with identical n, exhibit the same dispersive curves. The phase slopes at f0 flatten as n increases, hence generating wider phase shift bandwidth. Figure 3b shows that for the same Zm or Zb, but with different n, the stub impedance slopes are equal, while the impedance slope of the Zb branch is larger than that of the Zm branch since Zb >Zm. Table 1 shows that LL = 98.3 nH in the Zb branch for n = 4, almost twice that for n = 3, while the dispersive curve slopes are very close. Therefore, n = 3 is finally chosen.
The circuit topology and the fabricated prototype of the QHC are shown in Figure 4. The substrate has relative permittivity of 2.65, loss tangent of 0.002 and thickness of 1.0 mm. The strips connecting the ports are 2.575 mm in width, for a 50 Ω port impedance. All main-line and branch-line stubs share only one via, centered at the QHC, and the shunt capacitors of adjacent stubs are included in Cmb. All lumped elements are in 0402 type packages, producing an overall area of 4.5 × 4.5 mm2 (only about 0.6 percent the footprint of a conventional microstrip QHC with the same power split ratio). Due to microstrip discontinuities, the finalized chip values optimized using Ansoft HFSS (LRm = 3.6 nH, LLm = 15.0 nH, LRb = 15.0 nH, LLb = 47.0 nH, Cmb = 5.0 pF) are slightly different from the theoretical values listed in Table 1.
Measured and simulated S-parameters (see Figure 5) are in good agreement. Bandwidth closely corresponds, while an upward frequency shift of 58 MHz in the measured result is attributed to element tolerances. The measurement shows that |S11| = -20.7 dB, | S21| = -1.14 dB, |S31| = -11.34 dB, |S41| = -25.8 dB at f0 = 0.9 GHz, demonstrating Δ= 10.20 dB as well as good matching and isolation; with the relative phase difference ∠S21 - ∠S31 - 90° = 1.8°. Bandwidths defined by |S11| < - 15 dB, |S41| < - 15 dB, |S21| / |S31| - Δ = ± 1.0 dB and ∠S21 - ∠S31 - 90° = ± 5° are 46.7 percent, 47.4 percent, 34.3 percent and 41.7 percent, respectively, with the overlapping band ranging from 0.74 to 1.03 GHz, for a total relative bandwidth of 32.2 percent. Compared to a conventional microstrip QHC,8 this QHC features a broader bandwidth, significantly reduced footprint and a relatively high power splitting ratio; although, an additional 1 dB insertion loss is introduced along both the transmission and coupling paths due to inherent losses of the chip elements.
CONCLUSION
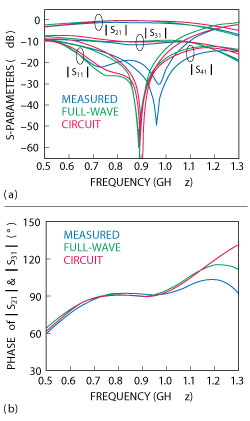
Figure 5 Measured and simulated S-parameters for the lumped SCRLH QHC with 10 dB power division ratio; magnitude of S11, S21, S31 and S41 (a) , phase difference between S21 and S31 (b).
A wideband QHC with a small footprint and an arbitrary power splitting ratio is demonstrated using a purely lumped SCRLH TL, by virtue of its nonlinear dispersion characteristics and smoothly distributed Bloch impedance. Its bandwidth is optimized with obtainable lumped chip elements. A prototype QHC with 10 dB power split ratio occupies only 0.6 percent the footprint of a conventional microstrip QHC, while achieving an overall bandwidth in excess of 32 percent.
ACKNOWLEDGMENT
This work is supported by the Fundamental Research Funds for the Central Universities under grant number K5051202007.
References
- X.Q. Lin, R.P. Liu, X.M. Yang, J.X. Chen, X.X. Ying, Q. Cheng and T. Jun, “Arbitrarily Dual-band Components Using Simplified Structures of Conventional CRLH TLs,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 7, July 2006, pp. 2902-2909.
- J.Q. Gong, C.H. Liang and B. Wu, “Novel Dual-band Hybrid Coupler Using Improved Simplified CRLH Transmission Line Stubs,” Microwave and Optical Technology Letters, Vol. 52, No. 11, November 2010, pp. 2473-2476.
- J.Q. Gong, C.H. Liang and B. Wu, “Compact Dual-band 90° Couplers with Customizable Power Division Ratios Utilizing SCRLH Transmission Lines,” Progress in Electromagnetics Research C, Vol. 36, January 2013, pp. 29-40.
- H. Okabe, C. Caloz and T. Itoh, “A Compact Enhanced-Bandwidth Hybrid Ring Using an Artificial Lumped-element Left-Handed Transmission-line Section,” IEEE Transactions on Microwave Theory and Techniques, Vol. 52, No. 3, March 2004, pp. 798-804.
- G. Sisó, M. Gil, J. Bonache and F. Martín, “Applications of Resonant-Type Metamaterial Transmission Lines to the Design of Enhanced Bandwidth Components with Compact Dimensions,” Micowave and Optical Technology Letters, Vol. 50, No. 1, January 2008, pp. 127-134.
- J.Q. Gong and Q.X. Chu, “SCRLH TL Based UWB Bandpass Filter with Widened Upper Stopband,” Journal of Electromagnetic Waves and Applications, Vol. 22, December 2008, pp. 1985-1992.
- P.L. Chi, “Miniaturized Ring Coupler with Arbitrary Power Divisions Based on the Composite Right/Left-Handed Transmission Lines,” IEEE Microwave and Wireless Components Letters, Vol. 22, No. 4, April 2012, pp. 170-172.
- D.M. Pozar, Microwave Engineering, 4th edition, Wiley, New York, 2012.
- C.L. Hsu, J.T. Kuo, and C.W. Chang, “Miniaturized Dual-band Hybrid Couplers with Arbitrary Power Division Ratios,” IEEE Transactions on Microwave Theory and Techniques, Vol. 57, No. 1, January 2009, pp. 149-156.
