Low power wireless sensors are receiving considerable attention due to their multiple applications in the commercial and military scenarios. Wireless networks of “power aware” smart sensors are being developed that are deployed and forgotten,1 as well as the sensor elements themselves. Transducers integrated with radio transceivers and networking intelligence are evolving through stages like “Motes,” “Dust,” “Pico Radio,” etc., to create maintenance free and autonomous sensors. A strong motivation to migrate from low power to zero power has been made apparent by the attempt to develop “ambient powered” smart sensors, with various techniques being proposed to harvest power from the surroundings.
The present work deviates from the traditional approach of developing zero power sensor elements by scavenging the environment for indigenous energy sources, be they mechanical, photonic, radio energy, acoustic, etc. However ingenious and efficient these techniques may be, power scavenging tends to encounter problems when the source of energy happens to be erratic or scanty.
The present technique proposes to illuminate passive sensors with RF energy and process the backscattered return signal to extract non-electrical information such as temperature, pressure, vibration, humidity, etc. Since the sensors are illuminated with a controlled source of RF energy, the inherent problem of power scavenging, such as the unpredictability of a local power source, is eliminated. The fact that the probing station needs DC power is alleviated due to the fact that such a station is capable of probing a multitude of totally passive sensors.
It is necessary to point out that the proposed technique is not based on the same principle that operates passive backscatter RFID tags,2 whereby the chip in an RFID tag gets powered by a reader. As seen in the following sections, the sensor element in the present technique is constructed from truly passive elements, unlike the so-called passive backscatter tag, which requires the use of a chip.
Fundamental Principle
The proposed technique is based on the following assumptions:
- Transducers are available whose change in electrical impedance can be correlated with some physical parameter such as temperature, pressure, vibration, humidity, etc.
- The impedance can be predictably characterized and modeled at sufficiently high RF frequencies by direct excitation as with a vector network analyzer.
- It is possible to measure the impedance remotely at those RF frequencies by processing the backscatter signal.
While the first two assumptions are valid for a variety of sensors, especially with various MEMS-based devices (such as mentioned in references3–10), the third assumption is not obvious.
Remote Measurement of Impedance by Backscatter
The fundamental principle for the measurement of an impedance by backscatter is illustrated in Figure 1. The area within the dotted box represents a standard FMCW radar.5 The voltage-controlled oscillator (VCO) output is swept over a certain band by a sawtooth waveform and radiated by an antenna A1. The propagating wave from A1 is received by another antenna A2, which is terminated by the impedance to be measured (device under test – DUT). In general, the DUT will not provide a perfect match to A2 and therefore will reflect part of the energy back to A2 and will be re-radiated. This so-called backscattered wave is now received by a receiving antenna A3, amplified by a low noise amplifier (LNA) and mixed with the transmit signal to produce an intermediate frequency (IF) signal.

Fig. 1 Fundamental principle of measurement of an impedance by backscatter.
The output x(t) from the VCO can be expressed as5–8

where
a(t) = incidental amplitude modulation of the VCO
s(t) = frequency modulating signal that is typically a sawtooth waveform
The instantaneous frequency f(t) is given by

where
f0 = start frequency
K = constant
The signal x(t) as expressed in Equation 1 is at the LO port of the mixer and the signal radiated from A1 is a scaled version of x(t).
If the instantaneous frequency f(t) is changing slowly compared to the reflection coefficient of the DUT Γ(f), the signal y(t) at the RF port of the mixer can be expressed as

where τ is the round trip delay and L is the effective loss between antennas A1 and A3 through A2, and Γ(f) = Γ(f) exp(ψ(f)) is the reflection coefficient of the DUT. L is assumed to be independent of frequency at the moment for simplicity, but in general is a function of frequency in multipath environment. The output from the mixer, after filtering, can be expressed as

The fact that the sweep is slow (usually of the order of milliseconds) compared to the round trip delay (usually of the order of nanoseconds) is used in simplifying the above equation. For the special case of a linear frequency sweep, Equation 4a becomes
The IF signal in such a case is a nominal sine wave with frequency

where
B = sweep bandwidth
TR = sweep time
The IF is then a modulated sine wave of carrier frequency
(B/Tr)τ with amplitude and phase modulation according to Γ(f(t)). In other words, a mapping occurs for the complex function Γ(f) from the frequency to time domain. Therefore, demodulation of the IF signal in Equation 4b provides information on the reflection coefficient between frequencies f0 and f0 + B.
Calibration
It is unlikely that the round trip delay τ and system loss L will be known accurately in a realistic environment and therefore needs to be calibrated out. In addition, system mismatches, multipath propagation, drift and temperature all contribute to inaccuracies that could be addressed using a calibration scheme. A simple scheme like the one shown in Figure 2 can be used for this purpose, where a typical reference impedance could be an open or a short. It is assumed that the amplitude offset α0 and delay offset τ0 between the test and reference channels are known accurately from a secondary measurement. It is reasonable to assume α0 to be independent of the frequency f.

Fig. 2 Calibration scheme.
In that case, the IF signals due to the test and reference channels are


Any cross-modulation terms have been neglected in the above treatment, as these can be maintained to negligible levels with proper design. It is obvious from Equations 6a and 6b that the test reference channels occur at different “carrier” frequencies, and so can be separated using traditional analog or digital filtering. By the judicious choice of τ0, it is possible to treat the signals as independent. Let ζ(t) be the equivalent complex analytic signal5 of a real time-domain waveform z(t) so that
ζ(t) = Re[z(t)] by definition (7)
The IF signals, as in Equations 6a and 6b, are in a low frequency range and can be converted to complex analytic signals by standard digital signal processing (DSP) techniques. As a result, from Equations 6a and 6b, one gets


Therefore,
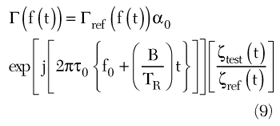
Sources of Error
The reference impedance, amplitude offset α0 and reference delay τ0 can be characterized accurately and designed so as to be drift free and quite insensitive to ambient conditions. However, for a free-running VCO, start and stop frequencies tend to drift with time and temperature and therefore need to be controlled accurately. From Equation 9, it is seen that the worst case phase Δφ error from the above effect is

where
Δf0 = uncertainties in start frequency
ΔB = uncertainties sweep bandwidth
In order to maintain the phase error within
![]()
the relation
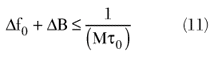
is needed
where
M = arbitrary large number
Equation 11 is a useful design equation requiring τ0 to be small to allow for a relaxed (large) frequency tolerance. This is in contradiction to the criterion for large τ0 desirable in discriminating between test and reference signals. It is seen that the requirement on frequency uncertainty is highly achievable since for a typical case of M = 100 and τ0 = 10 ns, the frequency accuracy needs to be within 1 MHz.
These could be achieved by precise frequency discriminators at the start and stop frequencies used to gate the transmit signal. Alternatively, a suitable phase-locked loop circuit could be designed to achieve this. Use of a frequency synthesizer needs to be dealt with caution, as continuity of phase is essential for this method to act properly.
As indicated earlier in this section, another possible source of error could be in the filtering process to separate the signals from the DUT and the reference impedance. The separation Df of the calibration and DUT frequencies, following Equations 6a and 6b, is given by Δf = τ0B/T; therefore, a high value of τ0B/T makes it easier to separate the two signals. Bandpass digital filters may be used to separate them, with due regard to the fact that the filters may produce different phase ripples and delays that need to be corrected for.
Additional Sources of Error
There are several other sources of error open to detailed investigation, as outlined below.
As evident from Equations 4a and 4b, nonlinearity in frequency sweep produces additional modulation on the IF signal on top of the one from the DUT itself, and its effect must be characterized.
The filtering of the IF signal is equivalent to range gating, and the technique inherently provides some degree of protection against multipath propagation. This needs more rigorous investigation as the assumption of a system loss L independent of frequency is an approximation at best.
System Loss
For a free space model with no multipath effects and bistatic configuration, the system loss can be expressed as4

where
G1 = gain of antenna A1
G3 = gain of antenna A3
R = distance between the target antenna A2 and the probe antenna A1 or A3 (assumed equal)
λ = wavelength
The radar cross-section s for this particular case is given by8

where
G2 = gain of the DUT antenna A2
F = fraction of the energy
re-radiated
F is a function of the impedance under test and losses incurred in the sensor. It can be expressed as

where
Z = impedance under test
Z0 = antenna impedance
Ls = losses associated with the total target element including those in the antenna A2
Based on these equations, it is seen that ranges of several meters would produce a carrier-to-noise ratio (CNR) of ~10 dB for a radiated power of a few milliwatts, an antenna gain of 10 dB in the probing station and 3 dB in the DUT, a detection bandwidth of a few tens of kilohertz, and an operating frequency of a few gigahertz. The effect of thermal noise can be reduced by multiple excitation and averaging.8
Application to Sensors
Now that the approach to remotely measure the impedance at RF frequencies has been outlined, two specific transducer elements will be given as examples to demonstrate the technique.
Surface-mount Thermistor
Consider a commercial NTC thermistor such as the TR series from RTI Electronics (Anaheim, CA), which is packaged in a standard surface-mount 0603 package. The 0603 package device can be approximately modeled as a series R-L circuit, with a parasitic inductance of approximately 0.7 nH in series with an NTC resistor. At a frequency of 1 GHz and an impedance environment of 50 Ω, Figure 3 shows the return loss and phase of the reflection coefficient as a function of temperature between –10° to +70°C, based on the described model and using the manufacturer’s data on the temperature dependent resistance.
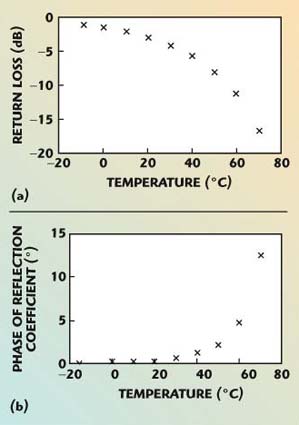
Fig. 3 Return loss (a) and phase of reflection coefficient (b) of a 250 Ω thermistor as function of temperature.
As the graphs show, at higher temperatures, the thermistor tends to provide a closer match to the antenna impedance and produces less backscatter. Therefore, measurement accuracy in this region would be primarily limited by the CNR, which could be improved by averaging. At lower temperatures, the change in reflection coefficient with temperature is small, and a need for good accuracy of measurement arises, although the CNR may not be an issue.
To make the variation of return loss with temperature (or any physical parameter) nominally linear, several approaches can be used. Use of fixed passive resistors in conjunction with the active thermistor, selection of the antenna impedance and tailoring of the temperature-resistance curve are some of the possibilities.
For a target temperature resolution of 2.5°C, a best-case amplitude accuracy of 0.1 dB (for low temperatures) must be attained. This is comparable to the state-of-the-art vector network analyzers.
Capacitive Pressure Transducer
Consider the other example of a MEMS pressure sensor10 based on the change of capacitance with pressure. The transducer changes capacitance approximately from 3 to 4.5 pF over a change of pressure of 500 to 1000 Torrs. At a frequency of 1 GHz or so, the device has a high Q, and can be approximately modeled as a pure capacitor. For the described change of capacitance, at 1 GHz, the phase angle of the reflection coefficient changes from 86.6° to 109.4° in an impedance environment of 50 Ω. Of course, the magnitude dynamic is not of a concern in this type of measurement, and phase accuracy is most important. For a realistic phase accuracy of 2°, a pressure resolution of the order of 50 Torrs is possible.
As shown by the above examples, it may be possible to monitor other physical parameters such as vibration, humidity, light flux, fluid flow, etc., using the described technique, as long as a transducer can convert the physical parameter into an electrical impedance.
Further Enhancements
In a practical environment, the transducer-antenna assembly may be mounted on or in close proximity to a large body that might reflect the radio waves. The “clutter” that might effectively reduce the dynamic range of measurement can be mitigated by putting a delay line between the antenna and the splitter. The clutter will thus be occurring at a different IF frequency and be removed by analog filtering.
The above property can also be used to perform “range gating,” whereby multiple sensor elements can be illuminated and processed simultaneously. The spacing between the sensors must be greater than the resolution criterion of c/2B4 to satisfy this mode of operation.
A need might arise to assign a unique identity (address) to each sensor, which can be achieved by using a unique impedance to each sensor as the reference impedance. The reference impedances can be pre-determined inductor or capacitor values instead of plain short or open circuits. In general, complex one-port networks may be used as reference impedances to create a very large number of signatures.11
So far, the discussions have been purely in the area of linear measurements. However, new avenues of information may open up if processing the nonlinear response from the sensors can be done. For example, certain crystals, under the influence of a magnetic field, generate varying proportions of even and odd order distortion depending on the ratio of DC and AC excitation in the magnetic field. It is to be noted that for the FMCW technique, harmonics generated in RF (at the sensor) can be made to generate harmonics in IF. In this way, the full nonlinear transfer function9 of the sensor can be characterized, which could give new insights to physical parameters. The calibration of such a system would be more complex, however, involving the use of a reference nonlinearity in the place of the reference impedance.
Conclusion
The approach being proposed herein is to use an RF signal to probe a truly passive sensor. The passive sensor contains a transducer that scatters back the signal quantified by the RF impedance, and therefore contains information about the characteristics of the physical parameter being sensed. To fully exploit the concept of a zero powered sensor, the transducer itself must not require DC power, but be capable of affecting the RF signal used to interrogate it. In this respect it has an advantage over power scavenging schemes, which assume the existence of ambient power. The sensor elements using this technique are expected to be extremely low cost and manufacturable on a large scale. The technique automatically provides range information, and can be adapted to provide bearing as well, resulting in identification of the location of individual sensor elements. A single probing station can thus handle a multitude of sensors. Numerous applications in industry, agriculture, environment, construction, medical, defense, etc., as well as consumer areas are envisaged. Scope for further investigation exists in development of MEMS-based sensors with appropriate characteristics in the microwave frequencies to be used with this technique.
References
- A.J. Goldsmith and S.B. Wicker, “Design Challenges for Energy-constrained Ad Hoc Wireless Networks,” IEEE Wireless Communications, August 2002, Vol. 9, No. 4.
- K. Finkenzeller, RFID Handbook, Second Edition, John Wiley & Sons Inc., Somerset, NJ, 2003.
- A.K. Henning, N. Mourlas, S. Metz and A. Zias, “A MEMS-based, High Sensitivity Pressure Sensor for Ultraclean Semiconductor Applications,” www.redwoodmicro.com/Papers/ASMC.pdf.
- M. Skolnik, Introduction to Radar Systems, McGraw Hill, New York, NY, 1984.
- S. Mukherjee, “Use of FMCW Techniques for Vector Measurement,” University of Kansas Doctoral Dissertation, 1989.
- D.R. Brunfeldt and S. Mukherjee, “Vector Network Analyzer,” US Patent 05307284, 1994.
- D.R. Brunfeldt and S. Mukherjee, “A Novel Technique for Vector Measurement of Microwave Networks,” 37th ARFTG Digest, Boston, MA, June 1991.
- F.T. Ulaby, R.K. Moore and A.K Fung, Microwave Remote Sensing, Active and Passive: Vol. II, Addison-Wesley, 1982.
- S. Mukherjee, “Vector Measurement of Nonlinear Transfer Function,” IEEE Transactions on Instrumentation and Measurement, August 1994, Vol. 43, No. 4.
- S. Tadigadapa and S. Massoud-Ansari, “Applications of High Performance MEMS Pressure Sensors Based on Dissolved Wafer Process,” www.mems-issys.com/pdf/issystech2.pdf.
- S. Mukherjee, “Passive RFID Tags,” Document Disclosure to US Patent Office, 2003.
