The inclusion of adapters and test fixtures in a measurement setup is often necessary even if the consequence is less accuracy. De-embedding the device characteristics has been traditionally the most effective method of minimizing the negative effects. However, the process of de-embedding has been a laborious, expensive procedure restricted to a laboratory environment. De-embedding has recently been automated to utilize the technique in both the laboratory and production environments. This article reviews S-parameter and vector network analyzer (VNA) fundamental concepts and describes the process of modeling adapters and de-embedding their effects. A summary of the advantages of using de-embedding techniques in a production environment is presented.


Measuring Non-insertable Devices

The potential for significant measurement errors must be addressed when measuring devices that are non-insertable. In a coaxial environment, a device under test (DUT) with a male-to-male or female-to-female connector configuration and devices with different connector styles are considered to be non-insertable. These types of devices are difficult to measure accurately because the test ports cannot be directly mated during the through calibration process without the addition of an adapter. A typical VNA calibration requires connection of a through device with zero electrical length and uses the information to correct for errors associated with the load match. However, if the electrical length of the through varies from calibration to measurement, then the phase relationship changes. As a result, the error correction for the load deteriorates. The amount of deterioration depends on the difference in line length between the two events. As a guideline, if the change in line length varies by more than one tenth of a wavelength, there will be no improvement in the load match compared to the system’s raw performance. If the difference in line length is a quarter wavelength, the system performance can be 6 dB worse than the raw uncorrected performance. At 10 GHz, one-quarter wavelength is about 0.3 inch, in air. This clearly demonstrates the need for minimizing the effects of adapters in measurements. It also illustrates how often removal of the adapter effect is needed. Any device that has a male-to-male or female-to-female configuration, or uses different connector types, needs some form of adapter removal technique applied. The most significant effects on measurements occur when measuring devices with poor return losses, such as at the output port of an amplifier, or devices with low insertion loss, such as cable assemblies. As will be seen, de-embedding the adapter is found to be the most accurate measurement method, and when the entire process is automated, such as with the system shown in Figure 1, the most practical.

Fig. 1  DCM COAX-3000 system with modeled adapters and de-embedding module.

Vector Network Analyzer Measurements

A well-designed vector network analyzer has the ability to provide very accurate measurements of the phase and magnitude of a signal over a broad frequency range. A primary reason for the accuracy is the ability to identify and remove the systemic errors inherent in the measurement system. The most popular method of error correction applied during VNA measurements is the twelve-term error correction, also known as a full two-port S-parameter calibration, and is possible due to the following capabilities:

  • Phase-locked frequency. It provides repeatable frequency performance characteristics over time. Frequency sensitive errors are correctable because errors measured at specific frequencies during calibration will be repeated during measurement.
  • Stability over time. Errors measured during calibration should not drift. The longer the system is stable, the longer the calibration remains valid. An additional caveat to calibration stability is test port connector wear and damage. As long as the test port remains intact, the calibration will be valid.
  • Stability over temperature. System characteristics should have minimal drift over the designated operating temperature range. Variations due to temperature drift should be specified in order to determine their effects on the measurement.
  • Ability to measure phase. This is the key attribute of the VNA and a primary reason for its accuracy. The effective measurement range of the VNA is much wider than for a scalar network analyzer due to its ability to identify and remove the phase and magnitude contribution of error signals.

Twelve-term Error Corrections

System errors exist in any measurement system. The following significant system errors, inherent in vector network analyzers, are found when the incident, reflected and transmitted signals are measured:

  • Directivity error: The lack of separation between the incident and reflected signals.
  • Reflection tracking: Variations in system response to the reflected signal.
  • Source match: How well matched the test port is to the transmission line characteristic impedance.
  • Transmission tracking: Variations in system response to the forward propagating signal.
  • Load match: The quality of the test port match when used as a termination for the reverse signal.
  • Cross talk: System leakages.

During calibration, six significant system errors are identified in both the forward and reverse directions giving the full twelve terms. The VNA is able to identify system errors by measuring known devices and comparing the measured results to the expected results. The calibration procedure then removes the extraneous error signals and provides the corrected measurements. For example, the directivity performance determines how well the coupler in the measurement system separates the reflected signal from the incident. If a coupler has a specified directivity of 40 dB, then the leakage signal will be 40 dB down from the incident signal and will define the limit of the reflected measurements. The magnitude and phase of the forward directivity leakage is measured during calibration by inserting a reference termination in port 1 and measuring the leakage signal at each calibration frequency. Notice that since the termination is not perfect, the signal measured will be a combination of directivity error and termination reflection. Since the directivity error is the dominant signal, it is possible to identify the phase and magnitude of directivity error down to the level of the termination leakage. During the error correction process, the VNA mathematically removes the identified directivity error. If the termination return loss is 60 dB, then the error correction process will improve the system directivity from the 40 dB hardware limit to an effective directivity of 60 dB.

The process of identifying the six system errors requires a set of known calibration devices attached to the test ports of the VNA, which in turn establishes the calibrated measurement planes. Note that the measurement plane can exist at the system front panel or at the end of a cable. The location of the calibrated measurement plane is established during the connection of the open and short reference devices. Typically, calibration is performed at the end of phase stable test port cables for various reasons. One is due to the requirement for connection of the two test ports during the through calibration. Test port cables also provide a means of extending the calibrated measurement port to the DUT.

Alternative Calibrations

The calibration process described thus far includes the connection of a short, open, load and through, and is commonly referred to as a SOLT calibration. As was seen, there are times, such as when a non-insertable device is being measured, when a direct through connection is not possible. There are also situations, such as using test fixtures or measuring on-wafer, when a quality termination is difficult to provide. Alternative types of calibrations have been offered in order to circumvent the requirement for terminations or through connections. Note that as long as the six terms are identified in both directions, then a full twelve-term error correction is still possible when using alternative calibration procedures. Following is a summary of the more commonly used alternatives.

Through Reflect Line (TRL)

This method uses a through, reflection and line length during the calibration process. The advantage of this method is the elimination of the need for a termination device. Any known reflective device, typically a short, can provide the reflection step. Since this method requires a through connection, it does not resolve the problem of measuring a non-insertable coaxial device.

Line Reflect Line (LRL)

LRL calibration does not require a through connection of zero electrical length for calibration. Instead, two known lengths of transmission line are used. This method is more commonly used for on-wafer rather than coaxial measurements. For coaxial measurements, the two line lengths need to be manufactured with high precision and mirror the same connector configuration as the device being measured. For example, if the device to be tested is a Type N male to 3.5 mm male, then two line lengths with Type N male to 3.5 mm male configurations are required. Although this process eliminates the need of the through calibration step, the line lengths are time consuming and expensive to produce. Also, a calibration kit for each device configuration needs to be produced and the method is bandwidth-limited.

Through-line Standard

This method uses the same basic components as the SOLT except that the calibration kit is modified to include a through line of known performance. The same limitations apply as with the previous alternatives; multiple devices must be manufactured, the devices must be accurately measured and the error correction model must be modified. Due to sensitivities of modeling techniques and bandwidth limitations, this procedure is only useful for frequencies up to 6 GHz.

Alternative VNA Measurement Methods

In addition to alternative calibration techniques, there are alternative measurement methods that have been used for adapter extraction:

Port Extension/Electrical Delay

This is usually performed from the VNA front panel operation. The technique mathematically moves the measurement plane towards the DUT by a given electrical length. This technique is a pure mathematical calculation and assumes that the adapter has no effects on the phase or magnitude of the incoming signal. Since this is never the case, the use of this function seldom provides satisfactory improvements and is typically only used as an electrical delay when analyzing phase variations in the DUT.

Direct Measurement

This is often cited as a method for calibrating test fixtures when used in a coaxial-to-microstrip situation. As mentioned previously, the difficulty is to provide accurate reference standards, which limits the effective directivity of the calibration. Also, notice that the through calibration is a concern since the probe tips cannot be directly connected. A preferred method is to characterize the test fixture using one of the alternative calibration techniques described, or removing the effects through de-embedding.

Adapter Substitution

During the open, short and load calibration, an adapter with the correct connector type for the device being measured is used. The electrical length of the adapter must be known. Then, when the calibration calls for the through connection, the adapter is removed and replaced with an adapter with an alternative connector configuration allowing direct connection of the two test ports. This second adapter must have the same electrical length as the adapter used during the previous calibration steps. This method minimizes the errors due to different electrical lengths but does not address the changes in impedances between the two adapters. This method requires extensive, well-defined adapter kits for each measurement condition, which are difficult and expensive to provide.

Time Domain

Time domain techniques can be used to measure the performance characteristics of a device after a one-port calibration. This is done by using the standard calibration devices of an open, short and termination. Note that a through connection is not required. For best results, the calibration and measurement need to be performed over as broadband condition as possible. This should be a minimum of 50 GHz for a 20 GHz device. During measurement in the time (or distance) domain, the port of the DUT is located and ‘gated.’ While using the gated function in the time domain, the fast fourier transform function (FFT) transfers the time domain information to the frequency domain and provides S-parameter information relative to frequency. This method can provide very good results; however, it is a complicated, labor-intensive procedure requiring careful planning and execution. It also requires a costly broadband system (50 to 60 GHz) with the appropriate calibration kits.

De-embedding

If the scattering parameters of an adapter are known, then the effects of the adapter can be de-embedded from the measurements mathematically. Since the method is a mathematical process, the results will be as accurate as the S-parameters used to model the adapter. Because of this, de-embedding can produce very accurate results and is the preferred method when available. The dilemma is that obtaining accurate S-parameters of the adapter is as challenging as measuring the non-insertable DUT. It has been found that characterizing the adapters using the time domain technique is the most accurate and practical method and the process has been automated in the laboratory.

Other reasons why the de-embedding process has not been more widely used are the effort needed to develop the algorithms in a software program and the time delay (refresh rate) when presenting the corrected data on a computer. Circuit modeling programs provide the ability to embed/de-embed networks for analysis purposes. However, they are not optimized for use in production or on the test bench in the laboratory. In order to make the de-embedding process more practical, a commercially available characterized adapter set and a program that automatically takes the S-parameters of the adapter, de-embeds the effects from the measurements and provides a real-time display of the results is needed. A commercial system is provided that includes the characterized adapters with data files, automatically downloads the adapter S-parameters into the software and de-embeds the effects. Also, to overcome the issue of time delay of the corrected display, the modified error models are automatically downloaded to the VNA, thereby providing a real-time display of de-embedded measurements on the CRT.

Fig. 2  Simplified representation of a two-port network.

Fig. 3 Flow-graph representation of a two-port network.

S-parameter Review

In order to understand the process of de-embedding, it is helpful to first review scattering (S) parameters. At low frequencies, circuits are typically characterized in terms of impedance, admittance and conductance (z, y and h). However, at higher frequencies, these measurements are often not practical. An easier method is to make swept-frequency, wideband measurements of the device with all ports terminated in their own characteristic impedances. S-parameters are a description of how well matched the ports are within the operating system when terminated by the characteristic impedance. Scattering parameters are defined as the ratio of the emerging to incident signals at each port. A two-port device can therefore be described by four S-parameters:

S11 – indicates how well matched port 1 is to the characteristic impedance of the transmission line.

S21 – is the forward transmission characteristics of the device.

S22 – indicates how well matched port 2 is to the transmission line characteristic impedance.

S12 – is the reverse transmission characteristics of the device.

Modeling a Two-port Network

Figure 2 is a simplified representation of a two-port network. The two-port device is connected to the output port of a signal generator and terminated by a load. In an ideal case, the source impedance ZS, the load impedance ZL and the system characteristic impedance Z0 are equal. Typically, the port impedances differ from Z0, and a portion of the incident signal is reflected due to the mismatch. The incident and reflected signals are represented on separate paths for clarity in this representation. Incident signals to any port N are denoted by the term aN. Signals emerging from port N are denoted by the term bN. S11 defines how well port 1 is matched to the characteristic impedance of the transmission line. S11 properties can therefore be measured by comparing the reflected signal b1 to the incident signal a1.

The two-port network may also be represented using signal flow graph analysis, as shown in Figure 3, and includes the four S-parameters. Each port has an incident and reflected signal associated with it. In the flow graph, the ‘a’ node of the port represents the incident signal and the ‘b’ node represents the emerging signal. S11 is given as the ratio of b1/a1. Note that two signals enter the b1 node, one from the a1 node and a second from the a2 node. Because a2 contributes to the b2 signal, it must be eliminated when measuring S11. The a2 signal is set to zero by terminating port 2 with a load of ZL = Z0. The conditions, which apply when considering S-parameters, can now be seen. Depending on the S-parameter, either the a1 or a2 signal must be set to zero. The bN signals and the S-parameters can now be defined as

           

A signal flow graph can be expanded to include all significant errors in a VNA system when considering the twelve-term error correction model (see Figure 4). Through algebraic manipulation of the equations derived from the signal flow graph, the error terms are modeled and extracted from the measurement. For a descriptive discussion on the twelve-term error model, see the referenced application note.1

The use of signal flow graphs is an excellent method for analyzing microwave networks. The graphs can model the most complex multi-port systems and provide an understanding of the interrelationships of multiple devices in a system. Also, a tool called the Mason’s rule can be used to simplify the complex signal flow relationship and reduce many of the algebraic manipulations. For further information on signal flow graphs and use of the Mason’s rule, the reader is referred to Adam2 and Mavaddat.3

Fig. 4  Signal flow-graph of a two-port network including measurement errors.

Fig. 5  Signal flow-graph of two cascaded two-port networks.

The De-embedding process

In order to address the technique of de-embedding, consider the signal flow graph of two cascaded two-port devices (see Figure 5). The composite SC11 parameter includes the S211 characteristics of the second device and therefore also includes the contributions of S121 and S112 of the first device as part of the new signal flow. Using Mason’s rule, the SC11 parameter is derived as

 

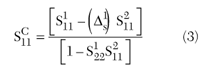
where

The process of analyzing cascaded multiple devices in a system can be further simplified by converting the scattering parameters to a new set known as the transfer scattering parameters or the T-parameters. The T-parameters are similar to the S-parameters, except that the signals seen at port 1 are now related to the signals at port 2. The differences can be diagrammed using matrix notation. The bN relationships are defined in Equation 1 for scattering parameters. The scattering matrix S of a two-port network is defined as

           

However, for the T-parameters, port 1 signals must be related to port 2 signals:

           

In expanded form:

           

Using Equation 1, a1 and b1 can be solved as:

           

where

Comparing Equations 6 and 7, the relationship of the T-parameters to S-parameters can be found:

          

The relationship between the S-parameters and the T-parameters can also be found:

          

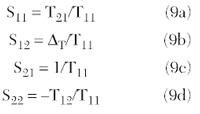
where

Fig. 6  Cascaded two-port networks using T-parameters.

The cascaded network now takes on the appearance shown in Figure 6:

In matrix form, these two networks are

           

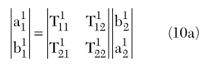
and

          

The combined network can be expressed by the single transfer scattering matrix:

           

The process of relating port 1 signals to port 2 signals allows the cascading of a series of devices using T-parameters and determining the overall relationships. By rearranging the scattering parameter relationships into the transfer scattering format, matrix multiplication can now be used when cascading multiple two-port networks. The overall scattering parameters of a cascaded network may be found using Equations 8 and 9 and expanding Equation 12 in terms of T-parameters. (For a more rigorous analysis, refer to Chapter 2 of Mavaddat3).

 

where

And in terms of S-parameters:

  

where

Finally, the relationship between the composite S-parameters, the S-parameters of the first device and the S-parameters of the second device, can be seen from Equation 14a–d. The composite S-parameters for the cascaded network are determined during the measurement process and the S-parameters for the adapter (the first cascaded device) are provided from the previous characterization process. The characteristics of the second cascaded device, the device under test, can now be determined through mathematical substitution. The converting of S-parameters to T-parameters, solving for the cascaded network, de-embedding the adapter and ultimately solving for the DUT is the procedure that is automated by the software. All that is required is the data file containing the adapter S-parameters, which can also be provided.

In summary, the process of de-embedding is simplified by using T-parameters. By using T-parameters, any number of two-port devices may be cascaded and quickly analyzed for total system performance. The overall scattering parameters can be determined by:

1.            Converting the S-parameters of each device to T-parameters

2.            Determining the combined T-parameters using matrix multiplication

3.            Converting the system T-parameters to composite S-parameters

Once the overall composite scattering parameters are known through measurement, and the scattering parameters for the adapter are known through characterization, the effects of the adapter on the composite measurement may be de-embedded to reveal the S-parameters of the device under test.

Additional Advantages for the Laboratory and Production

In addition to improvement in measurement accuracy, there are additional benefits using the adapter de-embedding technique. First, it is possible to change the test port connector type by simply adding the appropriate adapter (see Figure 7). The process of de-embedding moves the calibration plane from the end of the test port cables to the end of the adapters. Thus, it is possible to change the connector type by adding the appropriate adapter, activate the de-embedding routine and continue with the error corrected measurement without re-calibration. Reducing the frequency of calibration procedures helps to reduce potential errors from an improper calibration and is a significant time saver.

Fig. 7  De-embedding process by using modeled adapters.

A second major advantage using this technique is eliminating the need for multiple calibration kits. With a single calibration kit and multiple pre-characterized adapters, the VNA may now be calibrated and reconfigured for a wide variety of device configurations while reducing costs.

Conclusion

Removing adapter error contributions using de-embedding techniques can provide very accurate results. The success of the de-embedding process is determined by the quality of the adapter characterization. There are two challenges when implementing the de-embedding process: obtaining accurate characterization of the adapter and developing the software algorithm for the error extraction. In order to address the characterization concern, a one-port time domain measurement can provide accurate results when properly configured, although the process can be time consuming and require costly broadband measurement systems operating to at least 50 GHz. For the software algorithm requirement, circuit modeling programs exist that offer embed/de-embed routines. However, these programs are optimized for R&D development rather than for production or for the laboratory test bench. A software program and calibration system that automates the de-embedding process simplifies the procedure and provides the benefits with minimal effort. The automated de-embedding process now delivers benefits to both production and the laboratory. 

References

 1. “De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer,” Agilent Application Note 1364-1, 2001.
2.  S. Adam, “Microwave Theory and Applications,” Adam Microwave Consulting Inc., Los Altos, CA, 1992.
3. R. Mavaddat, Network Scattering Parameters, World Scientific, Singapore, 1996.
4. “Reference Data for Radio Engineers,” ITT Corp., 1964.
5. “10 Hints for Making Better Network Analyzer Measurements,” Agilent Application Note 1291-1B, 2001.

Steve Reyes is a graduate of the University of California, Davis, and has his MBA degree from the University of Santa Clara. He is currently a marketing consultant for DCM Industries Inc. He has been in the microwave test and measurement industry for more than 25 years and has held positions in product development and product marketing of microwave synthesizers, power meters, scalar and vector network analyzers. He has written and presented numerous papers and lectures on microwave measurements including power measurement lectures at the NIST/ARFTG Microwave Measurements Short Course.