
In the past, high frequency RF and microwave design engineers faced difficult choices when selecting an electromagnetic (EM) design and verification tool. The choices were often between a full-blown 3D EM tool with great accuracy but less than optimal simulation speed and design flow integration, or a planar EM modeling technology that offered simulation speed and design flow integration but often lacked the EM simulation power needed for designs that required characterization of 3D geometries. The new 2005 version of Momentum offers many new features and enhancements that tip the scale in favor of 3D planar EM design and verification.
With the new release, speed-versus-accuracy tradeoffs are addressed with the breakthrough enhancements in Momentum, a 3D planar EM simulator that accepts arbitrary design geometries, including multi-layer structures, and accurately simulates complex EM effects such as coupling and parasitics. Fully integrated into both the Advanced Design System (ADS 2005A) and RF Design Environment (RFDE 2005A) software packages, Agilent’s EM solver helps designers accurately characterize and improve passive circuit performance. The new additions and enhancements offers significantly improved capacity, accuracy and speed when designing and verifying passive components and interconnects for RFIC, MMIC and PCB/hybrid/ module design.
64-bit 3D-Planar EM Solver
The new, 64-bit version of the Momentum 3D planar EM simulator solves the capacity issue associated with large design and verification jobs by removing the memory limitations inherent with 32-bit applications. Thirty-two-bit computers are limited to a few gigabytes of memory, which restricts the size and complexity of the problems that can be solved. Designers were often faced with simplifying their designs to stay within the memory limitations, thus sacrificing accuracy. The new, 64-bit capability eliminates memory limitations and cuts EM simulation and verification time in half. This is valuable for the design and verification of large interconnect, package and antenna-array structures.
New Iterative Solver
Momentum now includes three unique solvers to address the varying degrees of EM modeling complexity and extend EM modeling efficiencies across a much wider application area. The Method of Moment (MoM) EM problem description, upon which Momentum’s solver algorithms are based, uses a linear system of equations that are compute-intensive when solving problems with a large number of unknowns. Momentum addresses this time-consuming process with an improved set of two traditional, direct linear systems of equation solvers and a new iterative Krylov subspace solver that makes it easy to simulate and verify large passive structures in a fraction of the time that is required with a direct solver. Momentum automatically chooses the appropriate solver for a given problem, depending on the problem size (number of unknowns), some other properties of the EM problem (especially ease and effectiveness of precondition for the iterative solver) and the platform/machine on which Momentum is running.
Direct Versus Iterative Solvers
The traditional direct solvers use a Gauss’ elimination algorithm type forming an LU decomposition of the square system matrix first, followed by a two-step sequence to solve the complete system. (Gauss elimination for a dense linear system is a process of order N3, with N being the number of unknowns.) This solve mechanism is very reliable and works for all types of problems, but the LU decomposition phase is expensive in terms of computation time because the process time grows with the cube of the number of unknowns in the system. This means that when using a direct solver for problems with a large number of unknowns, the time required for the solve stage of the simulation eventually dominates the entire simulation time. This can occur for problems of 5000 unknowns and above. It is especially true in the Momentum quasi-static solver (RF mode), where a single expensive load step for all frequency points is adequate, but a solve stage in all frequency points is required.
The iterative Krylov subspace solver does not require an expensive decomposition of the system matrix, but instead uses a sequence of matrix vector products to iteratively get a good approximation of the solution of the linear system. Krylov subspace methods allow many problems to get to the solution of the linear system using a small number of steps compared with the problem size (number of unknowns). Therefore, their computation time essentially depends on how efficiently a matrix vector product can be executed for a given problem. For linear systems with a dense system matrix, matrix vector products have time requirements that grow with the square of the number of unknowns in the system. For other, more compact matrix representations, computation time can improve further and result in algorithms with an order N log(N), or even an order N, time behavior. Figure 1 compares the computation times between the new Momentum iterative solver and the previous Momentum versions.

Fig. 1 The new Momentum Solver’s speed-ups versus the traditional versions.
Momentum Automatic Selection Mechanism
The direct solver is typically faster for small problems because it has a less costly setup time compared with the iterative solver. This faster setup, when the O(N3) behavior is not dominant, combined with the higher robustness, makes the direct solver the appropriate choice for small problems. It is often the best choice for slightly bigger problems as well, because of reliability, even when the direct solver is slower compared to the iterative solver. The decision to try the iterative solver only makes sense when the time required for the matrix-load stage is also considered and the total simulation time may drop considerably by using the iterative solver. Determining when to use the direct versus iterative solver is dependent on both the problem and the computer, and is not always an easy decision for the designer. Momentum automatically tests for this during the solve routine for the first frequency point. For typical machines in use today, Momentum always selects the direct solver below about 2000 basis unknowns. For larger problems, the iterative solver is tried first, but Momentum can switch back to the direct solver if it detects that the direct solver is going to be a better choice. Switching back to the direct solver may require recalculation time, but the computational cost is still less than that of adding an additional adaptive frequency sample point.
Improved Thick Conductor Modeling
Another major enhancement to Momentum 3D planar EM modeling is the addition of horizontal current modeling on the metal interconnect’s sidewalls as well as the vertical currents. This, in turn, provides full current modeling on all four sides of thick metal conductors, hence increasing EM modeling accuracy while no longer requiring the compute-intensive edge-mesh option to be turned on. An example is shown in Figure 2.

Fig. 2 An example of Momentum’s ability to model current distribution on all sides of thick metal conductors.
Modeling Horizontal Side Currents for Thick Conductors
Horizontal side currents for thick conductors can be modeled automatically in Momentum. This feature takes advantage of the Green’s functions, which represent the spatial impulse responses of the substrate, but does not require substrate database recalculation. The software allows the designer to visualize both the 3D mesh and the current distribution. When the horizontal side current toggle is set, the horizontal current components will be added on all conductors, which have been specified as automatically expanded. This results in a modeling of the current, as illustrated in Figure 3.
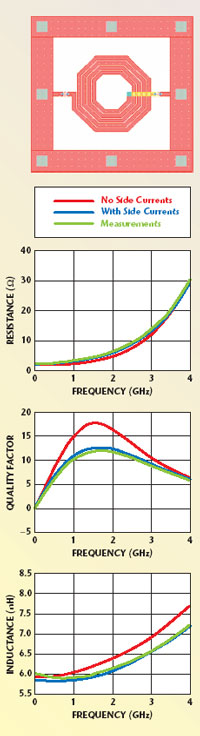
Fig. 3 Current densities modeled on all sides of a spiral inductor thick metal.
Improved Thin Layers Modeling
The Momentum modeling engine has been improved to better handle the thin substrate layers often found in Si-based process technologies. This new capability provides Momentum users with up to twice the simulation speed improvements for critical integrated components such as spiral inductors and metal-insulator-metal (MiM) capacitors. The new matrix-load mechanism is not only noticeably faster, but also increases the convergence accuracy. The example, shown in Figure 4, highlights these benefits by modeling a simple MiM capacitor design that exhibits thin-layer(s) next to a typical Si substrate. The results show not only much faster simulation times between the new Momentum version and the previous engine, but also demonstrate convergence to the correct answer with many fewer mesh cells.

Fig. 4 Modeling of a simple MiM capacitor design.
Conclusion
Momentum now covers a wider range of applications by adding breakthrough new technologies such as a new iterative solver alongside the full-wave and quasi-static direct solvers. It also offers an industry-first, 64-bit support, effectively removing the memory limits encountered in legacy 32-bit applications. These new technologies and enhancements give Momentum users faster and more accurate 3D planar EM modeling solutions. In certain cases, designers can expect to see speed improvements of up to ten times over previous versions.
Agilent Technologies,
EEsof EDA Division,
Santa Rosa, CA
(800) 829-4444,
www.agilent.com/find/eesof.
