Design of Microstrip Dual Behavior Resonator Filters: A Practical Guide

RF filters are commonly implemented inside receivers, with rigorous specifications about rejection of the adjacent transmitted frequency band, in order to preserve them from possible damage and degradation due to high transmit power.¹ Nowadays, these difficult problems are the subject of intensive studies in microwave planar filters.^2–5 For such applications, the use of dual behavior resonators (DBR) appears to be a very convenient solution because they allow the control of two attenuated bands on either side of one bandpass.^6,7 A DBR results from the association of two different parallel bandstop structures. Each of them brings its own transmission zero with respect to its fundamental resonant condition. At the same time, their association is transparent within a given operating frequency once the bandstop structures have been properly connected under constructive recombination criteria. It results in a bandpass response created between the above-mentioned lower and upper rejected bands. Quite often, a DBR filter can be an alternate solution whenever classical planar solutions are unable to solve a given problem.^8–18 This tutorial is aimed at showing how to benefit from this particular planar topology. The basic principles of DBR are recalled before describing in detail the design of a microstrip DBR filter in Ku-band.

What is a dbr

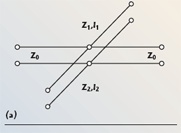
The generic structure, shown in Figure 1, can be described as a parallel association of two different bandstop structures of equivalent input impedances, Z_S1 and Z_S2. Obviously, the impedance of the whole structure is defined as

This equation shows that the stub association has no effect on the frequencies of the transmission zeros that always appear when Z = 0, that is when Z_S1 = 0 or Z_S2 = 0. The individual incidence of each bandstop structure is then preserved. Nevertheless, a bandpass can be created when the equivalent input impedances Z_S1 and Z_S2 have the same modulus, but become out-of-phase. Indeed, in this case, the total impedance, Z, tends towards infinity. According to the number of available parameters and to the initial behavior of each bandstop structure, a DBR allows the independent control of:

• 1 pole in the operating bandwidth

• 1 transmission zero in the lower attenuated band

• 1 transmission zero in the upper attenuated band

Such a structure can produce a response like the one shown in Figure 2. One should nevertheless keep in mind that spurious resonances appear on each side of the bandpass. Consequently, this kind of resonator is only usable over a limited frequency range.

DBR Filter Synthesis

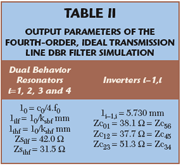
In planar technology, conventional bandstop structures can be easily implemented by using open stubs or short-circuited stubs, with or without stepped-impedances. Figure 3 shows some examples of DBRs. The first one, (a), is made of uniform open-circuited stubs of different lengths,^7,19 whereas the second one, (b), results from the combination of stepped-impedance stubs and open-circuited ones.^6,7 The third DBR structure, (c), is composed of uniform short-circuited stubs of different lengths,⁷ and the last one, (d), corresponds to an association of short-circuited stubs and open-ended ones.⁷ General syntheses, all based on classical slope parameter formalism, have been proposed.⁷ To illustrate the potential of a DBR filter, an ideal transmission line circuit (see Figure 4) has been simulated with Agilent-ADS.™

The simulated response produced (see Figure 5) is similar to that of a fifth-order DBR filter based on uniform-length, open-circuited stubs: a 4 percent fractional bandwidth centered at 1 GHz, with transmission zeros distributed symmetrically on each side of the bandpass. As an example, only the equations relative to the DBR n° 4 are given (see Figure 4), characterized by the parameters k_4lf and k_4hf equal to 0.91 and 1.09, respectively. These parameters define the position of the transmission zeros with respect to the central frequency. The proper slope parameter of this DBR is denoted by b4 and set to 1 here; b4 acts as a degree of freedom. Of course, the equations for the other DBRs are similar. It is worth noting that, because of the independence of DBRs, the transmission zeros are also independent. Flexibility is one of the great advantages of such a particular topology.

Design of a Ku-band Alumina Microstrip DBR Filter

Fourth-order Ku-band DBR Filter

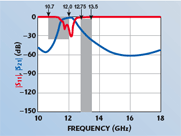
The design of a DBR Ku-band filter in microstrip technology will now be considered. This example will allow making explicit the design methodology, from the ideal transmission line model and associated synthesis to the manufactured circuit and final measurements. The focus will be on the particular features of this filter as well as on the difficulties met during the design. The proposed DBR Ku-band microstrip filter is slated to be incorporated in a receiver aboard a telecommunications satellite. Figure 6 gives its precise specifications with respect to frequency. This filter must be able to eliminate the transmit (Tx)-band without seriously affecting the very close receive (Rx)-band. The attenuation within the Tx-band, between 10.7 and 12 GHz, must be better than 35 dB. For the bandwidth defined within 12.75 and 13.5 GHz, the losses and flatness need to be better than 3 and 0.6 dB, respectively. No specifications are given for the frequencies located before the Tx-band and after the Rx-band. Therefore, the main problem here is to get better rejection while restricting the number of resonators to be used so as to reduce both the level of insertion losses and the structure size. Filter topologies including transmission zeros are obviously well suited to this kind of problem. Moreover, the lack of specifications outside the frequency band between 10.7 and 13.5 GHz makes the DBR topology appear as a good candidate.

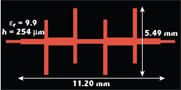
Until now, designers have usually developed classical hairpin filter solutions. Indeed, the electrical performance of a fifth-order hairpin filter built on alumina substrate (ε_r = 9.9, h = 254 μm) was found to meet the desired specifications for insertion losses, flatness and Tx-band attenuation equal to 2.30, 0.5 and better than 47 dB, respectively. With this solution, the overall size of the structure (6.6 × 2.9 mm²) remains small. However, this filter is very sensitive to technological variations because the smallest width for the slots is only 46 μm. Not only the sensitivity to dimensional variations, but also the influence of packaging must be considered with great attention. Since a fourth-order DBR filter should be sufficient to give the required out-of-band rejection, uniform-length stubs are chosen because of the availability of general synthesis⁷ and specific efforts are made to prevent the layout from having strong discontinuities. Tables 1 and 2 give the input and the output parameters chosen for the synthesis. Since no specifications were given for the frequencies located beyond the bandwidth, the high frequency transmission zeros were kept free. In order to simplify the design, all the DBRs were chosen identical. Finally, the degrees of freedom of the synthesis were used so that the stub- and inverter-impedances fell within 30 and 50 Ω. Such an impedance range provides a good compromise between insertion losses, rejection, dimensional sensitivity and junction-discontinuity size. Figure 7 shows the simulated response of the DBR filter with the input parameters given in Table 1. The next step is to build the equivalent microstrip circuit model, based on using an alumina substrate (ε_r = 9.9 and h = 254 μm) and shown in Figure 8. This model takes into account discontinuity effects, such as cross-junctions and open-end effects, as well as metallic and dielectric losses. Figure 9 shows the simulated response of the circuit and highlights the importance of the discontinuity effects to be overcome. The frequency of the transmission zeros can be adjusted by modifying the stub length, but this change is insufficient to tune the electrical characteristics in the bandpass. Moreover, such an electrical circuit model is not suitable in the present case, because it is unable to take into account the couplings between stubs, which strongly affect the response at these frequencies.

Figure 10 shows the electromagnetic simulation and the associated layout. The parasitic coupling effects clearly appear on the response. Transmission zeros are eliminated. Nevertheless, the electrical response can be improved to meet the desired specifications by carrying out an optimization procedure to correct the layout. This operation is easily done by changing the stub’s length to directly adjust the bandwidth and the attenuated band; the matching level is adjusted by modifying the impedances of stubs and inverters. The lengths of the inverters can be also used as tuning parameters.

Figure 11 shows that an acceptable matching level can be easily obtained, but with no full removal of the damages noticed on the attenuated band and flatness. It also compares experimental results with those of the electromagnetic simulation and shows that the insertion losses in the bandwidth are within 1.2 and 2.3 dB; moreover, attenuation in the Tx-band is better than 35 dB. So, even though the rejection satisfies the specifications, it is not true for the flatness value found to be 1.17 dB, and which must be improved. Figure 12 shows the layout obtained after further improvement. The filter size is 11.2 × 4.4 mm², and the smallest strip width is approximately 300 μm. It is worth noting that this layout is not significantly different from the one used in the original electromagnetic simulation.

Modified Fourth-order Ku-band DBR Filter

By strongly affecting the electrical response, the couplings between adjacent stubs are at the origin of a true limitation. It is clear that the change in the attenuation of the lower attenuated band is caused by the coupling between the low frequency stubs. It is the same for the upper attenuated band because of the coupling between the high frequency stubs. These effects are illustrated by substituting the stubs with microstrip coupled-line models in a circuit simulator. Figure 13 shows the frequency response obtained for a symmetrical second-order filter where symmetrical means two identical DBRs (a); the electrical response obtained after replacing the stubs with a coupled-line model (b); it makes clear the changes occurring in the response, especially those in the frequency regions of transmission zeros. Thus, a very convenient way to overcome damage in the lower attenuated band is to interchange the stubs; it results in the suppression of coupling phenomena in this frequency range (c). This action moves away the low frequency transmission zeros and, thus, widens the attenuated band. The difference of length between low and high frequency stubs now appears as a new tuning parameter. Figure 14 shows the layout obtained after a two by two exchange of the DBR stubs positions. Obviously, as in the previous case, a slight optimization phase is needed to adjust the response correctly. As shown in Figure 15, the new possibilities offered by such a configuration are used to improve the rejection in the lower attenuated band, and thus to significantly improve flatness in the bandpass. Once again, experimental and electromagnetic simulated results are in good agreement. The insertion loss within the bandwidth lies between 1.2 and 1.75 dB, and the attenuation in the Tx-band is greater than 40 dB. No significant change in the global size of the structure ensues from the geometrical change. Finally, this filter meets easily the required specifications.

Conclusion

The design of a DBR filter in Ku-band was described with rigorous specifications in terms of insertion losses, flatness and rejection. The solution offered sounds very convenient when there is no constraint outside of a limited frequency band of interest. The efforts were concentrated on the strong isolation between the adjacent Tx and Rx frequency bands, considered as the main critical point. The present study was aimed at describing the design methodology and demonstrating the possibilities offered by the DBR topology while focusing on the previously mentioned critical point. Compared to a classical hairpin topology, the proposed solution appears very attractive in terms of insertion losses, rejection level and sensitivity to dimensional variations. An improvement of approximately 1.2 dB in insertion loss was obtained by only lowering the order in the case of a DBR filter compared to that of a hairpin, that is a fourth-order (DBR) against a fifth-order (hairpin). Indeed, as the electrical specifications are met with a very large margin, the structure can withstand dimensional variations and dielectric permittivity tolerance over a large range of temperature amplitude; a spatial application may undergo temperature variations from –20° to 60°C. The study of the possible effects induced on the structure by packaging showed that, in the present case study, the addition of a metallic cover (h = 3 mm) made corrections unnecessary. Similar studies carried out for different frequency specifications, such as 10.7 to 12.75 GHz for the Tx-band and 13.75 to 14.8 GHz for the Rx-band, have led to similar overall performance. Moreover, the use of over-sizing techniques enables one to significantly reduce the size of a DBR structure to get closer to an equivalent hairpin structure or even smaller.²⁰ The main drawback of DBR structures is spurious resonances. Since they were not detrimental for the receiver case discussed here, however, no specific effort was done to suppress them. Nevertheless, in the prospect of other applications, this point has been the subject of thorough investigations, particularly through the integration of low pass structures in bandpass structure and coupled inverters.²¹ Among the other issues to be considered in the future, one should mention the stub coupling phenomena. They are not taken into account in the present synthesis, and doing it would simplify design and enhance performances. Alcatel Alenia Space has selected DBR solutions for use in telecommunications satellite receivers. The first one is used in a satellite, which is planned to launch in 2006.

References

1. I. Hunter, Theory and Design of Microwave Filters, The Institution of Electrical Engineers, Stevenage, Herts, UK, 2000.

2. J.T. Kuo, M.J. Maa and P.H. Lu, “A Microstrip Elliptic Function Filter With Compact Miniaturized Hairpin Resonators,” IEEE Microwave and Guided Wave Letters, Vol. 10, No. 3, March 2000, pp. 94–95.

3. G. Machiarella and A. Bovatti, “Single-sided Filters in Microstrip Technology,” 2001 European Microwave Conference Proceedings, pp. 45–48.

4. D.C. Rebenaque, A.A. Melcon and M. Guglielmi, “A New Simple Microstrip Open-loop Resonators Filter for High Selectivity Applications,” 2003 IEEE International Microwave Symposium Digest, Vol. III, pp. 1603–1606.

5. S. Amari, G. Tadeson, J. Cihlar and U. Rosenberg, “New Parallel l/2-Microstrip Line Filters With Transmission Zeros at Finite Frequencies,” 2003 IEEE International Microwave Symposium Digest, Vol. I, pp. 543–546.

6. C. Quendo, E. Rius and C. Person, “Narrow Bandpass Filters Using Dual Behavior Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. 51, No. 3, March 2003, pp. 734–743.

7. C. Quendo, E. Rius and C. Person, “Narrow Bandpass Filters Using Dual Behavior Resonators (DBRs) Based on Stepped-impedance Stubs and Different-length Stubs,” IEEE Transactions on Microwave Theory and Techniques, Vol. 52, No. 3, March 2004.

8. G. Prigent, E. Rius, F. Le Pennec, S. Le Maguer, C. Quendo, G. Six and H. Happy, “Design of Narrowband DBR Planar Filters in Si-BCB Technology for Millimeter-wave Applications,” IEEE Transactions on Microwave Theory and Techniques, Vol. 52, No. 3, March 2004.

9. C. Quendo, E. Rius and C. Person, “An Original Topology of Dual-band Filter with Transmission Zero,” 2003 IEEE International Microwave Symposium Digest, Vol. II, pp. 1093–1095.

10. A. Manchec, E. Rius, C. Quendo, C. Person, J.F. Favennec, P. Moroni, J.C. Cayrou and J.L. Cazaux, “Ku-band Microstrip Diplexer Based on Dual Behavior Resonator Filter,” 2005 IEEE International Microwave Symposium Session WE1F.

11. C. Quendo, E. Rius, A. Manchec, Y. Clavet, B. Potelon, J.F. Favennec and C. Person, “Planar Tri-band Filter Based on Dual Behavior Resonator (DBR),” 2005 European Microwave Conference Digest, pp. 269–272.

12. V. Palazzari, S. Pinel, J. Laskar, L. Roselli and M. Tentzeris, “Design of an Asymmetrical Dual-band WLAN Filter in Liquid Crystal Polymer (LCP) System-on-package Technology,” IEEE Microwave and Wireless Components Letters, Vol. 15, No. 3, March 2005.

13. W.H. Tu and K. Chang, “Compact Microstrip Bandstop Filter Using Open Stub and Spur-line,” IEEE Microwave and Wireless Components Letters, Vol. 15, No. 4, April 2005.

14. H.S. Wu, H.J. Yang, C.J. Peng and C.K.C. Tzuang, “Miniaturized Microwave Passive Filter Incorporating Multilayer Synthetic Quasi-TEM Transmission Line,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 9, September 2005.

15. M.I. Lai and S.K. Jeng, “A Microstrip Three-port and Four-channel Multiplexer for WLAN and UWB Coexistence,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 3, October 2005.

16. G. Macchiarella and S. Tamiazzo, “Design Techniques for Dual-passband Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 11, November 2005.

17. M. Ohira, H. Deguchi, M. Tsuji and H. Shigesawa, “Novel Waveguide Filters with Multiple Attenuation Poles Using Dual Behavior Resonance of Frequency-selective Surfaces,” IEEE Transactions on Microwave Theory and Techniques, Vol. 52, No. 11, November 2005.

18. C.M. Tsai, H.M. Lee and C.C. Tsai, “Planar Filter Design with Fully Controllable Second Passband,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 11, November 2005.

19. P. Rizzi, Microwave Engineering, Passive Circuits, Prentice Hall, Upper Saddle River, NJ, 1988, pp. 466–468.

20. A. Manchec, R. Bairavasubramanian, C. Quendo, S. Pinel, E. Rius, C. Person, J.F. Favennec, J. Papapolymerou and J. Laskar, “High Rejection Planar Diplexer Based on Liquid Crystal Polymer Substrate Using Oversizing Techniques,” 2005 European Microwave Conference Digest, pp. 101–104.

21. A. Manchec, C. Quendo, E. Rius, C. Person and J.F. Favennec, “Design Synthesis of Dual Behavior Resonator (DBR) Filters with Integrated Low Pass Structures for Spurious Responses Suppression,” IEEE Microwave and Wireless Components Letters, Vol. 16, No. 1, January 2006.

Eric Rius received his PhD degree in electronics from the Université de Bretagne Occidentale (UBO), Brest, France, in 1994, and in 1995 became an assistant professor within the department of electronics. In 2005, he became a full professor. His research activities within the Laboratory of Electronics and Communications Systems (LEST) include the design of filters and associated RF modules for microwave and millimetre-wave applications.

Cédric Quendo received his PhD degree in electronics from the Université de Bretagne Occidentale (UBO), Brest, France, in 2001. He is currently conducting research activities within the Laboratory of Electronics and Communications Systems (LEST). His research interests include the modeling and design of microwave passive devices for microwave and millimetre-wave applications.

Alexandre Manchec is presently pursuing his PhD degree within the Laboratory of Electronics and Communications Systems (LEST), Université de Bretagne. His research interests include the definition of new solutions for filters in planar technology.

Yann Clavet is currently working toward his PhD degree in electronics at the Université de Bretagne Occidentale (UBO), Brest, France. His interests include the modeling and design of microwave passive devices in multilayer planar technology.

Christian Person received his PhD degree in electronics from the University of Brest, Brest, France, in 1994. In 1991 he became an assistant professor in the microwave department of the Ecole Nationale Supérieure de Télécommunications de Bretagne/Groupe des Ecoles de Télécommunications, Brest, France. He became a full professor in 2003. He currently conducts research with the Laboratory of Electronics and Communications Systems (LEST). His research concerns the development of new technologies for microwave and millimeter-wave applications and systems. His activities are especially focused on hybrid three-dimensional (3-D) integration techniques for implementing optimized passives functions (filters, antennas, couplers) and improving reliability and interconnection facilities with active monolithic microwave integrated circuits (MMIC). He is also involved in the design of reconfigurable structures by means of MEMs or active hybrid circuits for smart antennas and software radio RF equipment.

Jean-François Favennec received his PhD degree in electronics from the University of Brest, Brest, France, in 1990. Since 1991, he has been an assistant professor with the Ecole Nationale d’Ingénieurs de Brest, France, where he teaches electromagnetic theory and microwaves. He currently conducts research with the Laboratory of Electronics and Communications Systems (LEST). His research activities include the modeling and design of passive devices for microwave applications.

Gaëlle Jarthon received her degree in electronics from the E.N.S.E.E.I.H.T, Toulouse, France, in 1995. From 1996 to 2001, she was an RF product design engineer with Alcatel, in charge of design and development for EHF receivers and beacons, Ka-band converters and new generations of receivers for telecommunications satellite payloads. From 2002 to 2003, she was a system engineer for Galileo Industries, Italy. Since February 2004, she has been an equipment program manager in charge of managing technical and programmatic aspects for export satellite prime customers.

Olivier Bosch obtained his DESS in microelectronics degree at Paul Sabatier University, Toulouse, France, in 2000. He joined Alcatel Space in 2000 as a planar microwave filter designer. He is also a MMIC designer.

Eric Rius

Jean-Christophe Cayrou graduated in electronics from E.N.S.E.A, Cergy, France, in 1989, and received his PhD degree in electronics from Paul Sabatier University, Toulouse, France, in 1993. He joined Alcatel in 1993, where he worked as a microwave design engineer in the microwave products department. He was in charge of contracts with several agencies (ESA, France Telecom CNET) interfaced with the SkyBridge system team. Since 1999, he has been head of the Receive Microwave Products Study group and the Advanced Microwave Products group, where microwave products such as C-/Ku-band receivers, Ka-band LNA assembly, Ka-band down-converter and up-converter assemblies, Ka-band LNA for FAFR antenna and the 44/8 GHz receiver have been developed.

Pascal Moroni received his degree in microwave engineering from the Université Paul Sabatier, Toulouse, France, in 1986, and obtained his Alcatel internal engineer degree in 2000. He joined Alcatel in 1988 and worked as a development technician on various equipment such as SSPA, active antennas and local oscillators. Since 2000, he has been in charge of the contract with CNES for the development of SiC components for SSPA. He is now in charge of the design of the new generation of Alcatel telecom receivers.

Cédric Quendo

Jean-Louis Cazaux received his PhD degree in physics and electronics in Toulouse, France, in 1985. He was then a post-doctoral research fellow at the University of Michigan, Ann Arbor, MI, in the field of advanced transistors and circuits for microwave electronics. He joined Alcatel Space in 1988 as a MMIC designer. Since 1996, he has been the head of the Microwave Advanced Studies within the Microwave Department. He acts as a reviewer and expert for the European Commission (IST) and the French Network for Research in Telecommunication (RNRT).