Technical Feature
Antenna Selection to Minimize Pointing Requirements
Traditionally, when designing a satellite communications system, an allowance is made in the link budget for pointing loss. The earth station's antenna size is then selected to achieve the desired gain margin. In this article, a different approach called antenna optimization (AO) is proposed, where the objective is to ensure that the antenna pointing requirements are kept to a minimum. For a given transmission system, when all parameters except the diameter of a single parabolic antenna are held constant, the allowable off-boresight movement is maximized when the budgeted pointing loss is 4.3 dB.1
Keith Willey
Cooperative Research Centre for Satellite Systems
University of Technology Sydney
Broadway, Australia
The use of low earth orbit (LEO) satellites for communications is increasing. The commercial success of these systems will depend, in part, on the consumer being able to purchase low cost earth stations. With higher data rates in demand, it is increasingly likely that these systems will operate at and above Ka-band. If an earth station uses a parabolic antenna, a pedestal is required to spatially track the satellite. Presently, tracking pedestals are relatively expensive and represent a significant portion of the total cost of an earth station.
A major factor in determining the ultimate cost of a tracking pedestal is its required pointing accuracy. As the pointing accuracy required increases so does the cost of the pedestal. A small pointing error budget may also increase the cost of calibrating and aligning the pedestal and antenna feed system. In addition, it may dictate the need for a more accurate orbital model or program tracking data. Thus, any technique that reduces the required pointing accuracy, and hence earth station cost, is desirable.
A reduction in pointing requirements can also produce benefits in a geostationary satellite system. In this case, the selection of the correct antenna may eliminate the need for a tracking pedestal or alternately decrease the satellite station-keeping requirements.
Traditionally, when designing a satellite communications system, an allowance is made in the link budget for pointing loss. The earth station's antenna size is then selected to achieve the designed gain margin. In this article, a different approach is proposed, where the objective is to ensure that the antenna pointing requirements, and hence the earth station cost, are kept to a minimum.
The interim antenna diameter D1 is determined by calculating the link budget, using a pointing loss of 0 dB. Then the antenna diameter is increased to a new value D2 . To close the link with the desired confidence level, the increase in gain DG between D2 and D1 represents the maximum allowable pointing loss. This can be used to calculate the off-boresight movement q for antenna D2 , which produces an attenuation of DG. The objective is to keep the link pointing requirements to a minimum. Thus, the optimum antenna size is the value of D2 that produces the maximum off-boresight movement q. For a parabolic antenna, this occurs when DG is 4.3 dB.
The off-boresight attenuation of a parabolic antenna can be approximated by a Gaussian function. Off-boresight attenuation =

This equation is scaled so that the half-power attenuation coincides with the 3 dB beamwidth. Converting to decibels gives the loss L(q) with respect to the on-boresight parabolic antenna gain in the direciton q as2

where
q3 dB = antenna 3 dB beamwidth calculated as2

where
l = carrier wavelength
D = antenna diameter
The difference in gain DG between two parabolic antennas with diameters D1 and D2 is

Combining Equations 2 and 3 and equating the off-boresignt loss L(q) to DG the expression for q becomes

Differentiating with respect to D2 and solving for

gives

Then, from Equation 4

This result is valid for any link where all parameters, except the diameter of a single parabolic antenna, are held constant, including both terrestrial and satellite links.
Analysis
|
|
|
Fig. 1 Allowed pointing loss vs. off-boresight movement as the antenna diameter is increased. |
Figure 1 shows the maximum allowed pointing loss versus off-boresight movement as the antenna diameter is increased for a link operating at 20 GHz. It shows the increase in antenna diameter in relation to D1 , the required antenna diameter when the link budget is calculated with a 0 dB pointing loss. For the link modeled, D1 is 1.2 m. Initially, as the interim antenna diameter is increased, the allowed off-boresight movement also increases until it reaches a maximum when the maximum allowed pointing loss is 4.3 dB. This occurs when the antenna diameter is 1.65 D1 .
An antenna larger than 1.65 D1 will increase the amount of allowed off-boresight loss in decibels, but decreases the allowed off-boresight movement in degrees. This is because the larger antenna has a narrower beamwidth compared to the smaller one. This results in higher attenuation for a given off-boresight movement.
Figure 2 shows the maximum allowed off-boresight movement to close the link versus the allowed pointing loss as the antenna diameter is increased for different carrier frequencies. It shows that all the curves reach a maximum when the budgeted pointing loss is 4.3dB. For the links modeled, D1 was assumed to be 0.3 m. Thus, for all frequencies, a 1.65 x 0.3 = 0.5 m antenna produces a budgeted pointing loss of 4.3 dB.
This analysis provides insight into the advantages and limitations of antenna optimization. It shows that at 20 GHz, a 0.38 m (2 dB budgeted pointing loss) antenna allows a maximum off-boresight movement of 1.14°, while a 0.5 m (4.3 dB budgeted pointing loss) antenna allows a maximum off-boresight movement of 1.28°. Thus, by increasing the antenna size from 0.38 m to 0.50 m the allowed off-boresight movement is increased by 0.14° or 12.3 percent.
|
|
|
Fig. 2 Allowed off-boresight movement vs. budgeted pointing loss different carrier frequencies. |
To achieve an increase in antenna gain of 4.3 - 2 = 2.3 dB the antenna diameter must be increased by 30 percent. However, in this case a 30 percent increase in antenna diameter only produces a 12.3 percent increase in allowed off-boresight movement.
For larger antennas, it is not practical to significantly increase the diameter to achieve a minor increase in an already small allowed off-boresight movement.
Note how the curves tend to flatten out as the frequency increases. This is due to the fact that a parabolic antenna's gain is a function of frequency. That is, for a particular parabolic antenna the higher the carrier frequency, the higher the antenna's gain and the narrower the beamwidth. As an antenna's beamwidth decreases, its off-boresight attenuation increases. It means the antenna size at which AO ceases to be practical, decreases as the carrier frequency increases. In other words, as the carrier frequency and antenna size increases, the penalty paid for using an antenna smaller than the optimum is reduced. In fact, at high carrier frequencies, depending on the antenna size, it may be more beneficial to suffer a small increase in pointing requirements to enable a considerably smaller antenna to be used.
If an off-boresight movement greater than that allowed using a 4.3 dB pointing loss is required, it cannot be achieved by increasing the antenna size and will need to be produced from another source (for example, an increase in transmit power).
The calculations above can be repeated using the actual beam pattern for a particular parabolic antenna (or a polynomial approximation of the actual beam pattern) allowing the exact optimum pointing loss to be determined. In a similar way, this technique can be used to determine the optimum pointing loss figure of antennas for which the beam pattern cannot be approximated by a Gaussian function.
Discussion
The traditional technique of designing a satellite communications system can still be used to determine the optimum antenna size to maximize the allowed off-boresight movement. This is done by simply including an antenna pointing loss of 4.3 dB in all link budget calculations. The optimum antenna size is then calculated in the usual way. The actual maximum allowed off-boresight movement for small angles (for a parabolic antenna) can then be calculated using a modification of Equation 5 as
Max off-boresight movement =
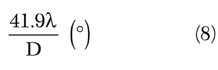
where
l = carrier wavelength
D = antenna diameter
Due to factors such as antenna diameter, carrier frequency or environmental restrictions it may not be practical to increase the antenna diameter to that required to provide a 4.3 dB pointing loss margin. In this case the antenna size should be increased as much as desired up to the 4.3 dB limit at which point the maximum allowed off-boresight movement can be calculated by
Max off-boresight movement =

where
L = budgeted pointing loss calculated using

+ original budgeted pointing loss (dB) (10)
Conclusion
This article shows that the required pointing accuracy is minimized when the antenna is chosen to produce a budgeted pointing loss of 4.3 dB. This result, which is called antenna optimization, provides real benefits in designing both terrestrial and satellite links. In the case of LEO satellite constellations, their commercial success will in part depend on the consumer being able to purchase a low cost earth station. Antenna optimization ensures that the required pointing accuracy and the cost of the earth station is minimized. In the case of geostationary satellite systems, antenna optimization enables the optimum balance between required transmit power and station-keeping requirements to be achieved. Appendix A offers two practical examples of AO.
Acknowledgment
This work was carried out with financial support from the Commonwealth of Australia through the Cooperative Research Centre program.
References
1. K. Willey, "Antenna Optimization to Minimize Pointing Loss," 6th Ka-band Utilization Conference , Cleveland, OH, June 2000.
2. G. Maral and M. Bousquet, Satellite Communications Systems , Third Edition, John Wiley & Sons, UK, 1998.
3. Sky Station International Inc. web page: http://www.skystation.com.
Keith Willey worked for 20 years in the television broadcast industry before receiving his bachelor's degree in electrical engineering from the University of Technology Sydney (UTS) in 1997. As part of his PhD research, he joined the Cooperative Research Centre for Satellite Systems at UTS. His area of research includes the spatial acquisition and tracking of LEO satellites operating at Ka-band. His work includes contributing to the design of the Ka-band earth stations being built by UTS.
Appendix A
The following examples demonstrate the use of AO in two practical situations.
Example 1
|
|
|
Fig. A1 Maximum allowed off-boresight movement as a function of antenna size. |
Assuming that a Ku-band satellite downlink is designed using the traditional link budget approach and is operating at 12 GHz with a budgeted pointing loss of 2 dB, the link budget calculations show that a 0.4 m parabolic antenna is required.
The maximum allowed off-boresight movement to close the link for different antenna sizes is shown in Figure A1 . The increase in antenna size produces an increase in the budgeted pointing loss, given by Equation 10:
For a 0.4 m antenna operating at 12 GHz, a 2 dB pointing loss equates to an off-boresight movement of 1.79°.
AO states that the maximum allowed off-boresight movement occurs when the budgeted pointing loss is 4.3 dB. This is achieved by increasing the antenna gain by 4.3 - 2 = 2.3 dB. Using Equation 4 the new antenna size becomes 0.52 m.
A 0.52 m antenna produces an allowed off-boresight movement of 2.01°. Thus, by increasing the antenna diameter from 0.4 m to 0.52 m the allowable off-boresight movement is increased by 0.22° or 12.5 percent.
Example 2
In this example, the use of AO in designing an earth station for the proposed Sky Station system3 is shown. The Sky Station's system consists of an unmanned, lighter-than-air platform that can be held geostationary in the stratosphere at an altitude of 21 km. A spectrum in the 47 GHz band has already been designated globally for such services.3
For the purpose of this example, the platform will be assumed to be kept in station within an area of 1 km diameter and that the earth station, which does not use mechanical tracking, is designed to use a 0.25 m parabolic antenna.
The most restrictive pointing requirements occur for an earth station that is directly under the platform. In this case, the platform will have a maximum off-boresight angle of 1.37°.
Using Equations 2 and 3 the antenna's off-boresight attenuation L(q) at angle q can be calculated as

where
freq = carrier frequency
c = speed of light
D = antenna diameter
For a 0.25 m parabolic antenna operating at 47 GHz the off-boresight attenuation at 1.37° is calculated to be 6.99 dB. Thus, using a 0.25 m antenna for the above system requires the budgeted pointing loss to be 6.99 dB. To calculate the optimum antenna size, the budgeted pointing loss is set to 4.3 dB. Then the required antenna diameter is determined to produce an off-boresight attenuation at 1.37° of 4.3 dB. This can be calculated by rearranging Equation A1 to form Equation A2 and substitute 4.3 dB for L(q).
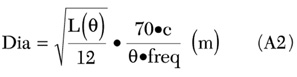

Thus, a 0.2 m diameter parabolic antenna is the optimum size for the specified system. The benefits of using a 0.2 m instead of a 0.25 m antenna include a reduction in the required transmit power or an increase in the area within which the platform must be kept in station.
If the station area is to remain the same, using a 0.2 m antenna allows a reduction in the required system gain of 6.99 - 4.3 + 20 log 0.2/0.25 = 0.75 dB. Equating this to the earth station transmit power, if 250 mW was required for the 0.25 m antenna only 210 mW would be required for the 0.2 m antenna.
Alternately, if the power required using the 0.25 m antenna is used with the 0.2 m antenna the diameter of the required station-keeping area is increased to 1.06 km.
This is an increase of 6 percent in the diameter or 12.4 percent in the size of the required station-keeping area. Station-keeping the platform within the required area represents a significant operating cost of the Sky Station system. Thus, an increase in the allowed station-keeping area has the potential to produce major cost reductions.



