Useful Filtering Techniques to Save Scarce Spectrum in Communications Systems
Helen Wright
Hewlett-Packard Co., Microwave Instruments Division
Santa Rosa, CA
Most communications systems fall into one of three categories: those that are bandwidth efficient, power efficient or cost efficient. Bandwidth efficiency describes the ability of a modulation scheme to accommodate data within a limited bandwidth. Power efficiency describes the ability of the system to reliably transmit information at the lowest practical power level. Cost efficiency means implementing a workable system with the lowest cost transmitters and receivers.
In most systems, bandwidth efficiency has a high priority. One powerful way to improve the bandwidth efficiency of a signal is to use filtering techniques. Filtering allows the transmitted bandwidth to be reduced significantly without losing the content of digital data, thereby permitting more users on a communications system and increasing revenue for the service provider. Some of the various types of filters used today are Nyquist or raised cosine, transmitter-receiver matched, Gaussian and Chebyshev equiripple finite impulse response (FIR). This article describes these filters and discusses the sharpness of a raised cosine filter, described by the filter bandwidth parameter a, which provides a direct measure of the occupied bandwidth of the system. In addition, various filter bandwidth effects are examined and their relative spectral efficiencies vs. power consumption are described.
Any quick transition in a signal (whether amplitude, phase or frequency) requires a wide, occupied bandwidth. Any technique that helps to slow these transitions narrows the occupied bandwidth. Filtering helps to smooth these transitions. The technique reduces interference by reducing the tendency of one signal or one transmitter to interfere with another in a frequency-division multiple access system. On the receiver end, reduced bandwidth improves sensitivity because more noise and interference are rejected.
Trade-offs in Filtering Techniques
Some trade-offs must be made in the system design to achieve optimum performance. One concession is that certain types of filtering cause the trajectory of the signal (the path of transitions between states) to overshoot in many cases. This overshoot can occur in certain types of filters (for example, Nyquist) and represents carrier power and phase. For the carrier to take on these values, it requires additional output power from the transmitter amplifiers (more than what is required to transmit the actual symbol). Carrier power cannot be clipped or limited (to reduce or eliminate the overshoot) without causing the spectrum to spread again. Since narrowing the spectral occupancy was the reason the filtering was inserted in the first place, the filtering technique can become a fine balancing act.
Other trade-offs are that the filter can make the radio more complex and bulky, especially if filtering is performed in an analog fashion. Filtering can also create intersymbol interference (ISI), which occurs when the signal is filtered to the extent that the symbols blur together and each symbol affects those around it. This effect is determined by the time-domain response (or impulse response) of the filter.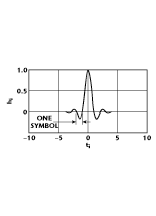
Figure 1 shows the time-domain or impulse response of a raised cosine filter(one class of Nyquist filter). A property of Nyquist filters is that their impulse response rings at the symbol rate. The filter is chosen to ring, that is, the impulse response of the filter crosses through zero at the symbol clock frequency. The time response of the filter travels through zero with a period that exactly corresponds to the symbol spacing. Adjacent symbols do not interfere with each other at the symbol times because the response equals zero at all symbol times except the center (desired) one. Nyquist filters heavily filter the signal without blurring the symbols together at the symbol times. This characteristic is important for transmitting information without ISI errors. Note that ISI exists at all times except at the symbol (decision) times. Usually the filter is split in half between the transmit and receiver paths. In this case, root Nyquist filters (commonly called root raised cosine) are used in each half so that their combined response is that of a Nyquist filter.
Sometimes filtering is desired at both the transmitter and the receiver. Filtering in the transmitter reduces the adjacent-channel-power radiation of the transmitter and, thus, its potential for interfering with other transmitters. Filtering at the receiver reduces the effects of broadband noise as well as interference from other transmitters in nearby channels. Figure 2 shows a set of matched filters in a typical transmitter/receiver.
To ensure zero ISI, both filters are designed so that the combined result of the filters and the remainder of the system is a full Nyquist filter. Potential differences can cause problems in manufacturing because the transmitter and receiver are often manufactured by different companies. The receiver may be a small hand-held model and the transmitter a large cellular base station. If the design is performed correctly, it produces the best data rate, most efficient radio and reduced interference and noise effects. For this reason, root Nyquist filters are used in receivers and transmitters as Ö Nyquist x Ö Nyquist = Nyquist. Matched filters are not used in Gaussian filtering.
In contrast, a GSM signal has a small blurring of symbols on each of the fours states because the Gaussian filter used does not have zero ISI. Wireless system architects must decide just how much of the ISI can be tolerated in a system and account for that ISI in addition to noise and interference.
Gaussian filters are used in GSM because they provide advantages in carrier power, occupied bandwidth and symbol clock recovery. The Gaussian filter features a Gaussian shape in both the time and frequency domains and does not ring like the raised cosine filters. Its effects in the time domain are relatively short and each symbol interacts significantly (or causes ISI) with only the preceding and succeeding symbols. This characteristic reduces the tendency for particular sequences of symbols to interact, making amplifiers easier to build and more efficient. Figure 3 shows a typical Gaussian filter response at 1.326 GHz.
The sharpness of a raised cosine filter is described by a. a gives a direct measure of the occupied bandwidth of the system and is calculated as
occupied bandwidth =
symbol rate x (1 + a )
If the filter had a perfect (brick wall) characteristic with sharp transitions and an a of zero, the occupied bandwidth would be
occupied bandwidth
= symbol rate x (1 + 0)
= symbol rate (for a = 0)
Ideally, the occupied bandwidth would be the same as the symbol rate, but this is not practical. An a of zero is impossible to implement. a is sometimes called the excess bandwidth factor because it indicates the amount of occupied bandwidth that is required in excess of the ideal occupied bandwidth (which is the same as the symbol rate).
At the other extreme is a broader filter with an a of one, which is easier to implement. In this case, the occupied bandwidth is expressed as
occupied bandwidth
= symbol rate x (1 + 1)
= 2 x symbol rate (for a = 1)
An a of one uses twice as much bandwidth as an a of zero. In practice, it is possible to implement an a below 0.2 and produce good, compact, practical radios. Typical values range from 0.35 to 0.50, though some video systems use an a as low as 0.11. Figure 4 shows the effects of a on filter bandwidth and shape.
The corresponding term for a Gaussian filter is bandwidth time product (BT). Occupied bandwidth cannot be stated in terms of BT because a Gaussian filter's frequency response does not extend identically to zero as does a raised cosine. Common values for BT are 0.3 to 0.5.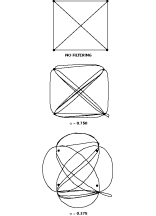
Different filter bandwidths exhibit different effects. For example, a quadrature phase-shift keying (QPSK) signal can be examined to determine how different values of a affect the vector diagram. If the radio has no transmitter filter, as shown in Figure 5 (at the top), the transitions between states are instantaneous. No filtering means an a of infinity. Transmitting this signal would require infinite bandwidth. The center figure is an example of a signal at an a of 0.750. The figure on the bottom shows the signal at an a of 0.375. The filters with a s of 0.750 and 0.375 smooth the transitions and narrow the required frequency spectrum.
Different filter as also affect transmitted power. In the case of an unfiltered signal with an a of infinity, the maximum (or peak) carrier power is the same as the nominal power at the symbol states. No extra power is required due to the filtering.
An example of a p /4 differential QPSK (DQPSK) signal as used in the North American Digital Cellular (IS-54) system is examined. If an a of 1 is used, the transitions between the states are more gradual than for an a of infinity and less power is needed to handle those transitions. Using an a of 0.5, the transmitted bandwidth decreases from two-times the symbol rate to 1.5-times the symbol rate. This change produces a 25 percent improvement in occupied bandwidth. The smaller a requires more peak power because of the overshoot in the filter's step response. This condition produces trajectories that loop beyond the outer limits of the constellation.
At an a of 0.2 (approximately the minimum of most radios today), there is a need for significant excess power beyond that required to transmit the symbol values themselves. A typical value of excess power needed at an a of 0.2 for QPSK with Nyquist filtering would be approximately 5 dB. This power level is more than three-times the peak power because of the filter used to limit the occupied bandwidth.
These principles apply to QPSK, offset QPSK, DQPSK and the varieties of quadrature amplitude modulation (QAM) such as 16, 32, 64 and 256 QAM. Not all signals will behave in exactly the same way and exceptions include frequency-shift keying, minimum-shift keying and any other signals with constant-envelope modulation. The power of these signals is not affected by the filter shape.
A Chebyshev equiripple finite impulse response (FIR) filter is used for baseband filtering in IS-95 CDMA. With a channel spacing of 1.25 MHz and a symbol rate of 1.2288 MHz in an IS-95 CDMA application, it is vital to reduce leakage to adjacent RF channels. This signal reduction is accomplished by using a filter with a very sharp shape factor using an a value of only 0.113. A FIR filter means that the filter's impulse response exists for only a finite number of samples. Equiripple means that there is a rippled magnitude frequency-response envelope of equal maxima and minima in the passband and stopbands. Figure 6 shows a typical Chebyshev equiripple FIR filter response. This FIR filter uses a much lower order than a Nyquist filter to implement the required shape factor. The IS-95 FIR filter does not have zero ISI. However, ISI in CDMA is not as important as in other formats since the simultaneous correlation of 64 chips is used to make a symbol decision. This coding gain tends to average out the ISI and minimize its effect.
The HP ESG series signal generators, shown in Figure 7 , allow designers to create signals using many different types of filters. Nyquist, root Nyquist, Gaussian FIR and IS-95 filters are available. These filter types can be selected and adjusted to meet a particular application. The filter a can be specified from 0 to 1; the BT for a Gaussian filter can be specified from 0.1 to 1. The FIR table editor enables designers to build custom filters for testing equalizers and add impairments such as static fading in the channel. Changing the filter factor may also be used to intentionally alter signal characteristics such as error vector magnitude.
Conclusion
For wireless systems designers, the goals of spectral efficiency and power consumption often compete with each other. As with any natural resource, it makes no sense to waste RF spectrum by using channel bands that are too wide. Therefore, narrower filters are used to reduce the occupied bandwidth of the transmission. Narrower filters with sufficient accuracy and repeatability are more difficult to build. Smaller values of a increase ISI because more symbols can contribute, thus tightening the requirements on clock accuracy. These narrower filters also result in more overshoot and, therefore, more peak carrier power. The power amplifier then must accommodate the higher peak power without distortion.
The bigger amplifier produces more heat and electrical interference since the RF current in the power amplifier interferes with other circuits, and larger, heavier batteries are required. The alternative is to have shorter talk time and smaller batteries. Constant envelope modulation - as used in Gaussian minimum-shift keying - uses class-C amplifiers, which are the most efficient. In summary, spectral efficiency is highly desirable, but there are penalties in cost, size, weight, complexity, talk time and reliability.
Helen Wright received an honors degree in electronic engineering from the University of Limerick (Ireland) in 1989. She has worked at Hewlett-Packard Co. for eight years as a product manager in marketing for fixed and mobile communications test equipment. Currently, she is the manager of the spectrum analyzer, source and network analyzer technical support group at the company's Microwave Instruments Division in Santa Rosa, CA. Wright has authored numerous articles and papers on communications test.