Today, we have continually increasing needs to move, recover, and decode data in smaller bandwidths and shorter time slots with reduced errors. We also want to detect higher resolution information in a physical world of increasing electrical interference. With us, has always been the problem of achieving sufficient signal to noise conditions for this to happen. In Marconi’s day, cranking up the power at the transmitter probably worked well enough to overcome noise. Timing didn’t matter much either since a string of short bursts of high and low tones could be decoded … as long as you could just tell them apart. Today, speeds are so high and modulation alphabets so complex, that lower and lower noise energy will affect us. And unlike Marconi, we have to keep cranking the power down. FM noise, PM noise, AM noise, multipath, random, stochastic… the list goes on. Just when you think you’ve got noise, there is more noise.
So noise is a problem. In radar, LO phase noise gets transferred to the downconverted signals, so if a large interfering signal is near a desired signal, the large signal’s phase noise skirt may overcome the wanted signal. Doppler radar attempts to detect moving objects against nearby, large stationary object clutter signals. Slow moving objects create close in Doppler signals and fast moving objects create far out Doppler signals. So you may have a phase noise issue of several proportions. A discrete spurious noise signal from a fan vibration may cause a spectral line perceived as a false target. In the A/D world of digitizing data, clock jitter will degrade the sampling timing and limit the number of bits accurately digitized. In digital communications, jitter will increase errors in sampling received data, and will reduce communication distances. But have no fear; superior engineering continues to deliver the goods despite the challenges of working with small signal energies in a noisy environment. The work being done at 60 GHz for wireless HDTV will soon move 3-6 Gbits/sec about my home while my bluetooth toaster is none the wiser and without interfering with my neighbor doing the same thing next door.
Reply to this Article
Read all responses
Win: The first five contributors are eligible to receive a complimentary copy of the textbook Electrical Engineering – A Pocket Reference from Artech House.
Types of Signals Needed
Reference frequency signals of different characteristics and agility are needed to perform these processes. I can’t tell you what spec limits to put on the frequency generating device you make or buy. Your system knowledge will define that. But always keep in mind that there are two parts to getting the job done. One is to choose the right oscillator and the other is not to noise up the signal as you put it to use in your system. For a microwave transmitter, your solution could be a nice quiet microwave oscillator made with a coaxial or cavity resonator. Or you may need better absolute frequency stability and choose a low noise VHF crystal based OCXO and use harmonic generators, filters, and amplifiers to generate your carrier. Or, with knowledge of your available system phase noise tradeoffs you may use a PLL multiplied solution to get some advantages of both types. For GHz speed digital signal design, you will have to interface to a world defined by jitter. You may have fewer options than the RF or microwave engineer has, since standard digital logic protocols, voltage levels, and waveforms rule. You might find advantages in the use of frequency control modules offering phase locking and jitter control in your system.
Focus of Topic
For the purposes of this short discussion, we’ll limit our focus on low noise, crystal based, oscillator and frequency module usage. To get started, I dusted off my old tree of instability factors for OCXOs, which is shown in Figure 1 with a few new tweaks. Here, factors are listed that can affect the stability or accuracy of an oscillator either from the perspective of specifying it or from the perspective of how your system affects the oscillator. The items listed in the circuit interface, modulating and random/statistical categories are the most pertinent to our jitter and noise discussion. The effects of these factors are both deterministic and random in nature. The deterministic problems are usually induced by identifiable causes such as power supply ripple or EMI. The random ones are from many physical processes of our circuit and physical resonator. Both of these show up as jitter in the time domain and phase noise in the frequency domain.
Figure 1: Tree of Instability Factors for OCXOs
Jitter and Phase Noise Representations
Figure 2A shows a signal in vector form with its associated noise vectors. At any point in time it can be modeled as a sum of its “original” vector and a noise vector that is a composite of all the noise signals present. If we sampled a signal at any exact repeated point in time we would get a “cloud” of answers that would represent all the sampled quantities of the signal vector’s value (Figure 2B). By analyzing the distribution and frequency of the values, we can characterize the phase noise, jitter, and amplitude noise present in the signal and understand their causes and possible improvements. Systems that measure phase noise or jitter do some form of this analysis.
To analyze jitter, we can strip off the amplitude variations and just look at the narrow slice of the cloud that represents the phase angle of the sampled vector. If the noise is random from many uncorrelated effects, then the distribution of phase values will be Gaussian, with many clumping near the ideal central value and less and less further away. By converting this jitter information to a rectangular plot with the phase errors expressed in time error, we can plot a histogram of the values (Figure 2C). The black line example is the Gaussian characteristic with random noise only. The orange and green examples have bi-modal or otherwise “extra” peaks of jitter from deterministic noise sources such as power supply ripple or subharmonic energy content. Identifying the different characteristics can help to troubleshoot for better system performance.
Figure 2: Noise Vectors and Jitter Hisograms
Conversely, we can analyze in the phase noise domain. Figure 3 shows in blue a “good” low phase noise signal. Shown also are examples of symptoms of vibration, power line noise, discrete spurs, etc. These are all interfering signals/conditions that you can impose on an “originally” good signal in your system. The red line’s overall curve shows the effect of analog multiplication on the signal. The phase noise increases at least 20 Log N (dB) where N is the multiplication factor. Using a PLL to multiply up may give a plot like the orange line. The phase noise will degrade or improve differently depending on the characteristics of the two oscillators and the PLL loop bandwidth. Division by digital divide is shown in green. Dividing will decrease phase noise much the opposite of multiplying, however, the noise floor of the divider may limit the noise floor.
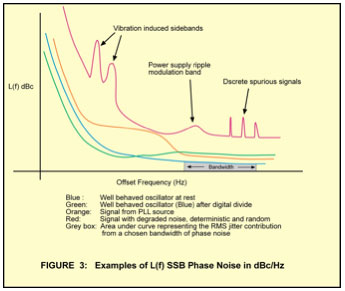
Figure 3: Examples of L(f) SSB Phase Noise in dBc/Hz
So what kind of crystal controlled frequency source will you design in? Our two categories are: 1) Simple low noise oscillators and, 2) Low jitter frequency control modules. The architectures of these items are compared in Figure 4. The oscillator is optimized for the single function of low noise and high stability. The module can lock to another signal and create outputs translated in frequency and of improved phase noise and jitter, and may have more functions such as multiple, selectable inputs/outputs.
Figure 4: Valpey Fisher Reference Oscillator and Frequency Control Module
Specification Choices and Usage
Many parameters will need to be specified for a purchased oscillator or module and you will need to optimize your system to best preserve and utilize the signal. We’ll focus on a few practical considerations pertinent to end result jitter and noise performance assuming you are designing in either a low noise crystal reference which may be multiplied to microwave frequencies or a phase locking jitter reduction module.
Frequency: For a reference crystal oscillator, often your best bet is at 100 MHz for overall good phase noise at a sufficiently high frequency so that subsequent multiplication is minimized. The oscillator supplier can use Hi-Q AT or SC cut resonators operating unmultiplied at 100 MHz. An excellent noise floor (beyond 10 KHz) of <-170 dBc/Hz is available. The close to carrier noise will be not as good as a 10 MHz oscillator; however, if multiplied, the extra multiplication would result in a worse noise floor.
For a module, you may not have a choice in frequency. Telecom and datacom interface frequencies often are standardized. This is not really an issue as these frequencies have a lot of product developed for them. For noise floor and cost considerations, the old practice of doubling your specified frequency and doing an up front divide by two for duty cycle optimization is not recommended.
Output Type:Sine wave into 50 Ohms is best for the lowest noise out of a reference oscillator. Design the functional circuit or device utilizing the signal to accept the oscillator signal as is without any intermediate amps or buffers as they will add noise. If you are using the signal to drive a number of devices, first try to optimize and protect the layout path to the point where the low noise is needed and then branch to other areas. Some ultra-low phase noise oscillators may have more load pulling than other oscillators due to a need to minimize internal buffer stages which each in turn add noise. Your loading should be well matched and “dead” with no other signals being back injected.
If you are choosing a module, you will likely be in the digital signal realm. For noise immunity, a differential signal such as PECL or LVDS is desirable since it can be distributed with good common mode rejection and the line impedance can be controlled. However, even though you are in a “digital” world, a sine output can be used to get the oscillator’s signal well traveled to its most critical end point. There it can be converted as required to digital formats.
Supply Voltage: Providing a power voltage of at least 5 volts or higher for a reference oscillator allows for good internal low noise design. Minimize the supply noise and ripple because some of it will get into the oscillator’s phase noise. De-sensitize your subsequent circuits to power supply changes so they do not post modulate the amplitude or phase of your signal. Remember to thoroughly de-couple the supply directly at the power input to the oscillator with bypass capacitors of several sizes. Observe the noise on this line and see what filtering gives the best reduction. If you are designing in a module, you will likely be limited to typical 3.3 V or similar digital logic supplies. So you likely won’t get to worry about choosing the value, but you will have to keep it noise free.
Vibration: Even high stability reference crystal oscillators specified for very low levels of acceleration sensitivity will have significant degradation of the phase noise under vibration (see Figure 3). Minimize vibration in all cases. It is worth your time to characterize the vibration frequency profile of your system. The internal structure of an oscillator design may have resonances where the vibration sensitivity will be amplified. With system profile specifications available, these can potentially be designed out or avoided. The acceleration sensitivity of the oscillator is a three dimensional vector quantity which is an effect of the resonator. In a critical case you can work with the oscillator manufacturer to control the direction of that vector and potentially orient it at right angles to the direction of your worst vibration displacement to minimize the vibration spurs or phase noise degradation.
Electronic Frequency Control: If you will not phase lock the oscillator, this should be taken into account. This allows the manufacturer to enhance the filtering on the voltage control port to a very low bandwidth and reject any noise you present to the EFC line. If phase locking, you should specify the modulation bandwidth that you need. Either way, you should be meticulous to keep wideband noise and discrete ripple off the EFC line as it will directly modulate the oscillator.
Spurious: Some otherwise low noise oscillators may have subharmonics and discrete spurs related to the process of creating (synthesizing) the output frequency you have requested. These may not be well specified by the manufacturer, so it’s a good idea to ask about what discrete spectral lines may be present in the output. I have run into a number of cases where this became an issue and delayed a project or caused a redesign.
Grounding and Layout: This topic offers a lifetime of learning. My advice: keep remembering that for high frequencies there is really no such thing as ground - or power - or anything else for that matter. Keep the power and ground structures as stable and signal free as possible. Layout realities will force compromises, so expect to pick your battles. Be cognizant of the relationship between the ground that the oscillator sees and the ground that your load device sees. Try to make them the same. Separate noisy lines from your low noise signals.
I’ve found it helpful to map out how different circuit portions flow their current to the ground. I like to keep the larger and noisier ground currents from flowing through the grounding structures of my more critical low noise circuit portions. Steer the ground currents of unrelated functional circuit sections (i.e. RF vs. logic controls) around each other to some benign final grounding point rather than just connecting to a ground plane at any old place. I tend away from Vcc power planes and use sectionized Vcc fingers to serve particular circuit portions. Locally bypassed fingers can help to commonize the noise between ground and Vcc. Remember that the capacitance of every signal trace to a ground plane is a significant part of your high frequency circuit. With capacitive sensitive CMOS waveforms, removing the ground from under these traces can help maintain rise and fall times and mitigate the effect of any shifting trigger levels at a receiving device. When implementing a filter, going straight to a ground plane for each grounding point, or to a concentrated ground structure, may create blow by and foil your filter. The grounding for the filter should be allowed to flow along with the filter elements.
Jitter: When specifying noise in the world of digital modulation and encoding, jitter is often the currency of the realm. Like phase noise, jitter energy exists over a bandwidth of frequencies. If jitter is only important in a certain band of frequencies (such as outside of a downstream PLL’s bandwidth) Then it is best to specify it in a RMS value over the critical band of jitter frequencies (See Figure 3). An example is the SONET methodology of specifying allowable jitter in the 12 KHz to 20 MHz BW. Specifying peak to peak jitter is seldom useful because random jitter does not have a well defined peak to peak value. Specifying RMS jitter, either as total wideband jitter, or band limited jitter is a more meaningful specification. As we have said, equally important is that you don’t jitter up your “purchased” clean signal. Keep in mind the power supply cleanliness and circuit layout where the signal runs. If you do a good job, the quantization noise at your receiver will define the floor level of effective jitter. Any ground noise (deterministic or random) or power noise that can shift the relative voltage level where the receiver triggers from the rising edge will add to this and increase jitter. This may be from extraneous signal crosstalk or EMI coupling. Also, the logic voltage supplies and grounds will have significantly varying current in them from all the devices being powered. Uncorrelated switching currents from other devices can effect trigger threshold levels on another device and create a timing jitter. Good signal integrity will always be to your advantage to minimize this. Try to maintain the fastest rising and falling edges of the signals to the receiver and the least waveform distortion.
Jitter Attenuation: Often frequency modules are used for the purpose of reducing jitter of a noisy signal such as a recovered clock from a digital data stream. The reduction in jitter can be significant. Jitter above the module’s internal PLL bandwidth is effectively filtered off and the outputted jitter is only equal to the internal VCO. Jitter within the PLL’s bandwidth is passed through. A jitter transfer function can therefore be defined. As a side benefit, the internal PLLs can be set up to output other required frequencies with the same jitter reduction. An advantage of the complete module is that the manufacturer is able to optimize the VCXO crystal for the best performance in the loop to enhance the device noise floor. Most VCXOs purchased separately on the market have limited phase noise performance and will not result in the same amount of jitter attenuation.
Hopefully you will make good use of frequency control devices in your designs and get rich and famous on your successful, well-functioning circuits. If not, I offer the sage words of a college professor of mine who would often hear a frustrated young engineering student at the test bench lament that “this circuit doesn’t work!” He would very calmly and wistfully say: “A circuit always does what it is supposed to do.”
Dan Nehring is VP of engineering at Valpey Fisher Corporation, a pioneer in the design and manufacturing of precision crystal oscillators. Valpey Fisher develops precision timing devices for high frequency applications requiring the lowest phase noise. In addition to their series of TCXOs, VCXOs, and XOs operating at 1.0GHz, Valpey Fisher offers complete timing modules, commercial oscillators, Hi-Rel/COTS oscillators, and VCOs to provide the precision timing required in optical networking, wireless infrastructure, test and measurement, and avionics.
References
Hewlett Packard, Phase Noise Characterization of Microwave Oscillators, Product Note 11729B-1.
H. Hausman, The Effect of High Stability Reference Oscillators on System Phase Noise, Microwave Journal, February 2005.
D. Nehring, Quartz Frequency Control Devices for Wireless Base Stations, 1995 RF Design EXPO Proceedings.