Dual-band Assembly of Integrated Short Backfire Antennas

The short backfire (SBF) is a highly effective aperture antenna of simple and compact construction. Basically, it consists of three elements: two parallel reflectors, large and small, spaced a half-wavelength apart, which form a leaky resonant cavity, and a cavity feed (half-wave dipole,^1–3 waveguide or horn,^4,5 or microstrip antenna^6,7). The large and small antenna reflectors are usually circular in shape and have diameters that may vary within the ranges (1.5–2.3)λ₀ and (0.3–0.65) λ₀, respectively. However, from classical gain, bandwidth, match and size considerations, the large reflector is typically set to 2λ₀ and the small reflector to 0.5λ₀. The dipole feed is positioned at the mid-point between reflectors, that is at a distance 0.25λ₀ from each of them. Here, λ₀ is the antenna resonant (design) wavelength. As a rule, the large reflector is fit with a quarter- or half-wavelength wide rim, which results in side lobe and back lobe pattern reduction and a gain increase. The SBF antenna dimensions given above are based on the extensive experience of many researchers⁸ and provide the reference for this work. Henceforth, they are referred to as standard dimensions. Although often circular, the backfire reflectors can have various shapes: polygonal (square, hexagonal, octagonal), elliptical, etc. The short backfire antenna has been used extensively as a directive building element in various single-band broadside arrays.^9,10 A dual-frequency assembly (array) of two short backfire antennas (large or LF and small or HF) is described in this article. The antennas are arranged on the same axis and, since they have a common reflector, are regarded as integrated. In this way, the following advantageous effects are achieved. First, the common reflector plays two roles at once: as a small reflector for the LF antenna and as a large reflector for the HF antenna. Second, the blocked aperture region, resulting from the small reflector of the LF antenna, is exploited for the HF antenna. Such integration makes the SBF assembly simple to build, compact and robust. For standard radii of the disk reflectors, the low and high design frequencies of the two dipole-fed antennas should be in the standard proportion 1:4^.1,2 Circular (disk) reflectors are frequently replaced by polygonal, and, in particular, by octagonal reflectors, which are close in shape to the circular ones and are very practical for construction.^11,12 This article’s first author originally introduced the dual-band assembly of two integrated octagonal short backfire antennas.⁸ This SBF antenna system was employed 25 years ago in an UHF earth station for satellite tracking and space telemetry that operated at the frequencies 137 and 470 MHz, that is for a reflector design frequency ratio of 1:3.43, which differs from the standard frequency proportion. At that time, the dual-frequency SBF antenna assembly was designed based on approximated analytical equations and was optimized experimentally by means of the conventional “cut and try” routine. The work reported here started with the design of a single 3 GHz SBF antenna with octagonal reflectors. The resultant numerically obtained radiation parameters were checked against experimental ones for a SBF antenna with circular reflectors,³ and found equivalent in gain. This allowed a validation of the design procedure. Next, the SBF antenna design and numerical procedures were extended to the axial arrangement of two integrated octagonal SBF antennas, large and small, and tuned respectively at 1.2 and 4.8 GHz, according to the optimum frequency proportion of 1:4. In contrast with the previous dual-band SBF antenna development, the availability of specialized electromagnetic tools, such as the method of moments (MoM)-based WIPL-D software,¹³ now allows a more rapid, thorough and precise design process.

Basic geometry of two integrated short backfire antennas

Figure 1 shows the basic configuration of a dual-frequency assembly of two integrated SBF antennas, stacked along the Z axis. The disk reflectors are specified as R₁, R₂ and R₃. They have radii r₁, r₂ and r₃, correspondingly, which are chosen here equal to the standard values

where λ_1,0 and λ_2,0 are the two design wavelengths.

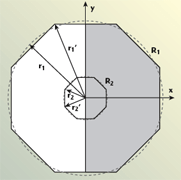
The reflector doublets R₁R₂ and R₁R₃ form the two open SBF resonant cavities (antennas) C₁ and C₂ of axial lengths h₁ ≈ 0.5 λ_1,0 and h₂≈ 0.5 λ_2,0, respectively. Thus, the total antenna length is h = h₁ + h₂ ≈ 0.625 λ_1,0 ≈ 2.5 λ_2,0. The second disk reflector R₂ is common to the two antenna cavities and acts as a small reflector for the cavity C₁ and a large reflector for the cavity C₂, that is the two SBF cavities (antennas) are integrated in one double-frequency structure. The cavities are fed by single-wire half-wave dipoles, F₁ and F₂, respectively, and are matched to their feed cables at the design frequencies f_1,0 = c/λ_1,0 and f_2,0 = λc/λ_2,0. Here, c = 3 10⁸ m/s is the free-space wave velocity. From Equation 1, it follows that the frequency ratio k_f= f_2,0/f_1,0 is equal to four as is the ratio between the disk radii, r_I/r_I+l = k_f = 4, i = 1,2.

Computer-aided design: validation of the methodology for single short backfire antenna with octagonal reflectors

Figure 2 shows the half portion of the 3D computer simulation model of a single SBF antenna. The antenna comprises two octagonal reflectors, the rimmed large reflector R₁ and the planar small reflector R₂, made of a metal sheet of thickness t = 2 mm. The leaky cavity formed by the reflectors is fed through a half-wave dipole F positioned in the middle of them. The reflector rim has a half-wavelength width. The general n-sided polygonal reflector is regarded as a good approximation to the disk reflector when both have equal surfaces.¹³ This condition is satisfied if the j-th (j = 1 or 2) polygonal reflector is inscribed into the corresponding circle of equivalent radius r'_j given by

where r_j is equal to r₁ = λ₀ or r₂ = 0.25λ₀, the radius of the respective large and small circular reflectors, where λ₀ is the design wavelength.

In the case of octagonal reflectors n = 8 and r'_j = 1.054r_j, and thus, for the single octagonal reflector SBF antenna, Equation 1 yields

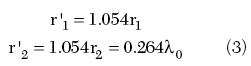
The circular reflectors of radii r₁ and r₂, and the equal-in-surface octagonal reflectors of radii r'₁ and r'₂, respectively, are projected together in the transverse plane x0y, as shown in Figure 3. A design frequency of 3 GHz was chosen to compare the computational results with the reliable experimental data for a SBF antenna that, as part of separate research, was built and measured at AFCRL.³ The present numerical treatment considers octagonal reflectors designed according to Equations 2 and 3, and the analysis was made by means of the WIPL-D electromagnetic software. The measured and numerical dimensions and radiation parameters of the circular SBF prototype and its equivalent octagonal model are summarized and compared in Table 1.

The WIPL-D simulated numerical patterns of the 3 GHz octagonal model and the experimental patterns of the corresponding AFCRL circular prototype are shown in Figure 4 for the E-plane and the H-plane cuts. As seen, the octagonal-reflector antenna has numerical radiation parameters very close to those measured for the corresponding circular-reflector prototype. This provides evidence that Equations 1 and 3, introduced by the authors, and the numerical simulation procedure, are well suited for the design of equivalent octagonal reflector SBF antennas and assemblies. The resonant input resistance of the free-space located single-wire feed dipole, with a 0.005 to 0.01 radius to lambda ratio, ranges from approximately 60 to 70 Ω and is therefore roughly matched to a 50 Ω cable. But, placed between the two reflectors, its input resistance decreases to approximately 17 to 20 Ω, which corresponds to a VSWR of 3.0 to 2.5. A better input match can be achieved by using an appropriate matching device, which may cause additional antenna loss and bandwidth reduction. The present work has shown that, in the case of a short backfire antenna, a very good input match to a 50 Ω cable is possible by using one of the following two techniques: a feed antenna with much greater free-space input resistance, 300 Ω folded dipole, for instance,¹⁴ or a small deviation from the standard half-wavelength SBF antenna length. In both cases, the feed dipole is positioned in the middle between the reflectors.

The input match for three versions of the SBF antenna is illustrated in Figure 5, where the reflection coefficient S₁₁ is drawn versus the frequency. Case 1 is for a standard-size SBF antenna fed by a single-wire half-wave dipole with a diameter of 1.5 mm and a length of 20.7 mm, or equal to 0.207λ. For the design frequency f₀ = 3 GHz, S₁₁ is –7.25 dB. This corresponds to a VSWR (at f₀) of 2.45, or to a mismatch power loss of 0.9 dB. Case 2 is for the same standard-size SBF antenna but fed by a folded two-wire dipole, 5 mm in width and 17.5 mm in length. The first dipole wire, in the center of which the feed terminals are located, is 2 mm in diameter, while the second dipole wire has a diameter of 1.5 mm. In Case 3, the SBF antenna is similar to that of Case 1 with the only difference that the antenna length is slightly increased for better impedance match: from 0.5λ₀(50 mm) to 0.56λ₀ (56 mm). The minimum or design frequency values of S11 in Case 2 and Case 3 are smaller than –40 dB, which is far below the –10 dB level. It is known that the free-space single-wire half-wave dipole has a smaller input bandwidth than the corresponding folded (two-wire) dipole. Placed in the cavity of the increased-length SBF antenna, the single-wire dipole has a bandwidth of 6.2 percent, which is much greater than the bandwidth of 2.8 percent for the SBF antenna fed by the folded dipole. The SBF antenna rim width is not very important for the input match quality, but it plays a key role for the antenna gain, radiation pattern shape and polarization. If ω = 0, the SBF antenna with octagonal reflectors has a gain of 13.2 dBi, which is 1.8 dB below the gain of the SBF antenna with a half-wave rim (see Table 1).

Design of two integrated short backfire antennas with octagonal reflectors

Based on the previous results, a system of two integrated SBF antennas (see Figure 6) is considered, comprising three octagonal rather than circular reflectors, R₁ and R₂ (rimmed) and R₃ (not rimmed), and two half-wave dipoles as feeds, F₁ and F₂. As was found from Equation 2, in the case of octagonal reflectors r'_j = 1.054r_j, and thus Equations 1 are modified here to

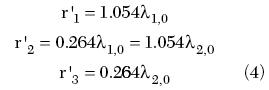
In Table 2, the basic dimensions of a dual-band assembly consisting of two SBF integrated octagonal antennas are summarized for the respective design frequencies (wavelengths): f_1,0 = 1.2 GHz (λ_1,0 = 250 mm) and f_2,0 = 4.8 GHz (λ_2,0 = 62.5 mm). The reflector radii r'₁, r'₂ and r'₃ have been calculated from Equations 2 and 4, and the half-wave rim widths w₁ and w₂ of reflectors R₁ and R₂ were set to 0.25λ_1,0 and 0.5λ_2,0, respectively. For the given dipole-wire radii, a₁ = 0.008λ_1,0 and a₂ = 0.008λ_2,0, the rest of the dimensions, that is the individual antenna lengths h₁ and h₂ and the feed-dipole resonant lengths l₁ and l₂, were found by computer optimization for best possible gain and input match to a 50 Ω cable. In both antennas, a good input match was produced by a small increase of the standard half-wavelength antenna length, 5.2 percent for the LF antenna and 16.2 percent for the HF antenna. As seen from Table 2, the optimum antenna lengths h₁ and h₂ expressed in the corresponding design wavelengths are different, which is due to the dissimilarity in their rim widths w₁ and w₂, joint antenna positioning and electromagnetic influence. The total antenna length includes also the second reflector thickness t₂, or h = h₁ + h₂ + t₂. In order to increase the compactness of the overall design, the rim of the large reflector R₁ was chosen as λ_1,0/4, whereas for the HF antenna, gain improvement results from choosing the rim of the common reflector R₂ as λ_2,0/2. The radiation patterns of the optimized single and integrated octagonal short backfire antennas are subsequently presented. Figure 7 illustrates the co-polar (a) and cross-polar (b) 45°-plane gain radiation patterns of the 1.2 GHz single and integrated SBF antennas. As seen from these figures, the integrated short backfire antennas have radiation patterns that do not differ much from those of the single backfire antennas. The co-polar 45°-plane patterns of the single and integrated antennas are close except in the side lobe regions, where the electromagnetic shadowing by the small antenna causes approximately a 5 dB increase in the side lobe levels. It is found that the antenna integration produces a gain reduction of only 0.2 dB and a maximum cross-polarization increase of 1.4 dB. Similar co-polar and cross-polar radiation patterns of the single and integrated 4.8 GHz antennas are shown in Figure 8. Here the integration does not produce a gain reduction but a gain enhancement of 0.4 dB. This apparent inconsistency in the gain behavior may be attributed to the difference in the rim widths and to the dissimilarity in the electromagnetic shadowing and mutual input coupling. Because the feed dipoles of the two SBF antennas are well isolated by their leaky wave cavities, the mutual coupling between the two feed ports is very small, less than –50 dB at the LF port and less than –35 dB at the HF port.

In both LF and HF SBF antennas, the size adjustment resulting from the optimization process does not significantly deteriorate the original or standard-size antenna radiation patterns. Figure 9 and 10 show the co-polar radiation patterns of the 1.2 GHz and 4.8 GHz integrated SBF antennas in three cut planes: E-plane, 45°-plane and H-plane. It is seen that the main lobe of the 1.2 GHz antenna has an almost rotational symmetry, which does not hold for the 4.8 GHz antenna main lobe and for the side lobes of both antennas. In the HF antenna, a significant side lobe reduction compared to the LF antenna is produced, ranging from 3 to 15 dB in an angular region of 150°. Figure 11 compares the corresponding co-polar and cross-polar 45°-plane radiation patterns of the 1.2 and 4.8 GHz integrated antennas. From the co-polar patterns, it is obvious that the HF antenna has a 1.2 dB larger gain and much lower secondary lobes and back-to-front ratio. In contrast, the LF antenna has a broader and lower level cross-polar pattern in the main lobe area.

Finally, the 3D co-polar and cross-polar gain patterns are plotted in Figure 12 for the 1.2 GHz integrated antenna and in Figure 13 for the 4.8 GHz integrated antenna. The basic antenna parameters of the single (non-integrated) and integrated SBF antennas are summarized in Table 3, which also specifies the match and bandwidth antenna properties. The integrated SBF antennas have a very good resonance input match and frequency bandwidth, which are better than those of the non-integrated SBF antennas matched also by means of antenna length optimization.

Conclusion

An assembly of two axially integrated short backfire antennas, tuned at frequencies in a ratio of 1:4, was described and studied numerically. An approximate design equation for dimensioning the SBF antenna octagonal reflectors is proposed and combined with a MoM-based electromagnetic analysis tool for a numerical design, size optimization and antenna parameter analysis. The thorough numerical examination of the antenna assembly has demonstrated that it is not only compact and simple to build, but also possesses attractive properties for many applications, such as a double-band operation, a reasonable gain of approximately 14 to15 dB, good linear polarization and match characteristics. For both antennas, mismatch losses less than 0.05 dB at the design frequency, and less than 0.45 dB over the frequency band of approximately 6 to 7 percent, have been attained by means of the proposed antenna length-variation technique. The approach may also lend itself to the design of circular polarization antennas by using two orthogonal feed dipoles.

Acknowledgment

H.D. Hristov and R. Feick gratefully acknowledge the financial support received under the Chilean Conicyt/Bicentenario Project ACT-11/2004.

References

1. H.W. Ehrenspeck, “The Short Backfire Antenna,” Proceedings of the IEEE, Vol. 53, No. 4, August 1965, pp. 1138–1140.

2. H.W. Ehrenspeck, “A New Class of Medium-size High Efficiency Reflector Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 22, No. 2, March 1974, pp. 329–332.

3. H.W. Ehrenspeck and J.A. Strom, “The Short Backfire Antennas as Element for High Gain Arrays,” Report AFCRL-71-0234 Air Force Cambridge Research Laboratories, Bedford, MA, April 1971

4. A.C. Large, “Short Backfire Antenna with Waveguide and Linear Fields,” Microwave Journal, Vol. 19, No. 8, August 1976, pp. 49–52.

5. M.S. Leong and P.S. Kooi, “Rectangular-waveguide-excited Short Backfire Antenna with Corrugated Rim,” Electronics Letters, Vol. 15, No. 17, August 1979, pp. 533–535.

6. A.A. Kishk and L. Shafai, “Gain Optimization of Short Backfire Antenna with Different Excitation Types,” 1986 IEEE Antennas and Propagation Society Symposium Digest, pp. 923–926.

7. C.D. Kaloi, D. Hatfield and P. Simon, “Microstrip Backfire Antenna,” 1981 IEEE Antennas and Propagation Society Symposium Digest, pp. 343–346.

8. A. Kumar and H.D. Hristov, Microwave Cavity Antennas, Artech House Inc., Norwood, MA, 1989.

9. H.W. Ehrenspeck and J.A. Strom, “Short-backfire Antenna-A Highly Efficient Assembly Element,” Microwave Journal, Vol. 20, No. 5, May 1977, pp. 47–49.

10. A. Andersson, P. Bengtsson and A. Molker, “Short Backfire Antenna Arrays for Space Communications,” 1977 IEEE Antennas and Propagation Society Symposium Digest, pp. 194–197.

11. L.R. Dod, “Backfire Antennas for Telemetry and Tracking Applications,” Proceedings of the 1969 NTC, Washington, DC, 1969, pp. 77–84.

12. O.M. Woodward, “Short Backfire Antenna with Sum and Error Patterns,” US Patent 4240080, December 1980.

13. WIPL-D Pro v5.1, 3D Electromagnetic Solver, WIPL-D d o. o., 2004.

14. H.D. Hristov, J.R. Urumov, R. Feick and G.S. Kirov, “Dual-band Array of Integrated Short Backfire Antennas,” accepted for presentation, 2006 ANTEM/URSI International Symposium, Montreal, Canada.

Hristo D. Hristov received his PhD and DSc degrees in radio engineering from Technical University, Sofia, Bulgaria. Since 1965, he has been with the Technical University of Varna, Bulgaria. He is currently a research professor with Universidad Técnica Federico Santa María, Valparaíso, Chile. He was a researcher at the Strathclyde University of Technology, Queen Mary College and the Eindhoven University of Technology. His research interests include high frequency electromagnetism, antennas, propagation, microwave devices and wireless communications.

Rodolfo Feick received his degree in ingeniero civil electronico from Universidad Técnica Federico Santa María, Chile, in 1970, and his MSc and PhD degrees in electrical engineering from the University of Pittsburgh in 1972 and 1975, respectively. He has been with the department of electronics engineering at Universidad Técnica Federico Santa María since 1975, where he is now the head of the telecommunication group. His research interests include wireless systems and data communications.

Jordan R. Urumov graduated from the St. Petersburg Electro-technical University, Russia, in 1972. He received his PhD degree from the Technical University of Sofia. In 1990, he became associate professor in the department of radio engineering, Technical University of Varna, Bulgaria. His research interests include high frequency electromagnetism, antennas, propagation, microwave circuits and devices, optoelectronics and optical communications.

Georgi S. Kirov received his MSc and PhD degrees in radio engineering from the University of Varna, Bulgaria. In 1969, he joined the department of radio engineering and, in 1999, became the head of the department. From 1981 to 1986, he was with the University of Setif, Algeria, as a lecturer in the field of telecommunications. He specialized in microwave antennas at Moscow Technical University and the Moscow Technical University of Communications and Informatics. He also was a researcher at the University of Magdeburg, Germany. His research interests include high frequency electromagnetism, antennas and wave propagation, microwave/optical devices and wireless communications.