In addition, the array moves and scans along the horizontal (x) direction (see Figure 1 and Figure 5), resulting in a two-dimensional planar array formed by electrical scanning in elevation and mechanical scanning in azimuth. The d_x and d_y dimensions are essentially the same. Electrical scanning in the vertical (y) direction and motion scanning in the x direction form a two-dimensional array. The ideal two-dimensional detection array has a uniform arrangement of detection elements in both the x and y directions as shown in Figure 4. The imaging algorithm is based on the uniform arrangement of x and y elements, and the calculation methods for x and y directions are essentially the same. Figure 6 is a photograph of the linear array.

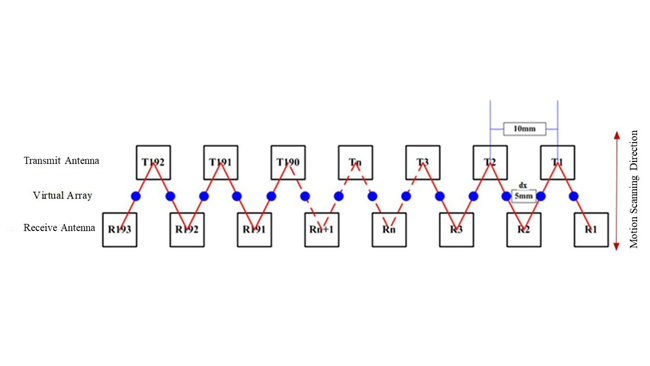
Figure 4 Linear array antenna layout.

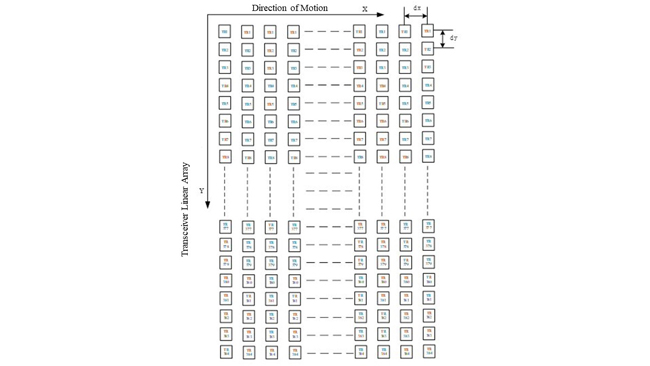
Figure 5 Mechanical scanning of the linear array antenna.

Figure 6 Photograph of the linear array antenna face.

Simulation is used to determine the effects of array distribution errors on PSLR and ISLR. In this model, d_x represents the sampling point interval in the x direction and d_y represents the sampling point interval in the y direction. Electrical scanning in the y direction and mechanical (motion) scanning in the x direction form a two-dimensional surface scan. The distribution error of sampled points in the surface scan is composed of distribution errors in both directions.

Processing accuracy mainly determines the uniform distribution error of sampling points in the y direction. High machining accuracy leads to small uniform distribution errors, while low machining accuracy leads to large uniform distribution errors.

In the x direction, the array shakes with the movement of the scanning frame, which causes uncertainty in the sampling point position. The motion accuracy of the scanning frame determines the degree of motion jitter and determines the uniform distribution error of sampling points in the x direction.

Whether it is the uniform distribution error of sampling point positions caused by machining accuracy or the motion jitter of the scanning frame, the uniform distribution error of sampling point positions impact image quality. Image quality is measured by three factors: image resolution, PSLR and ISLR.

Figures 7 and 8 illustrate the effects of errors in the horizontal direction on imaging. The model uses a uniform distribution error σdx (see Figure 7). A simulation is also conducted to show the effects of a Gaussian error distribution N(μ, σ) dx on the quality of the image (see Figure 8). For the Gaussian distribution N(0,0.25), 95.6 percent of the data is distributed between −1 and 1, which supports the practicality of using an error of N (0,0.25) dx for array simulation. In Figures 7 and 8, the scattering points are located at the center of the coordinate system and the simulation results show a dynamic range of 30 dB.

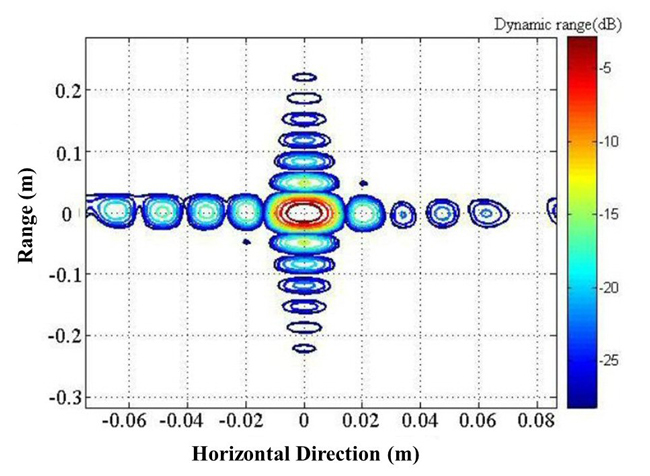
Figure 8 The effects of N(0,0.25) Gaussian distribution errors in the horizontal direction on imaging.

The influences of uniform and Gaussian error distributions on PSLR orientation (horizontal and vertical axes), PSLR range and ISLR are shown in Table I. The mmWave image starts to demonstrate distortion with a uniform distribution error (−0.3dx, 0.3dx). While PSLRs are not significantly impacted, the increase in ISLR with a uniform error distribution indicates increased energy leakage from the main lobe to the sidelobes. To ensure imaging accuracy, the array error should be less than 10 percent.

EFFECT OF SPECTRAL ERROR AND LINEARITY ERRORS ON IMAGE RESOLUTION

Spectral error and linearity are both caused by the imperfect performance of mmWave sources. However, spectral error and linearity measure the deviation of the transmission frequency from different perspectives. The collected LFM waves are discrete frequency points, and the spectral error is the deviation ^df between adjacent frequency points. The spectral error emphasizes the uniform distribution of transmission frequency point intervals. Linearity emphasizes the nonlinear error of linear frequency modulation waves. These two errors indicate that the linear frequency modulation wave not only grows linearly but also needs to be evenly distributed.