Solid-state (i.e., semiconductor based) generated radio frequency (RF) used to power processes and applications has taken hold in the last couple of years in a number of markets and has given rise to the notion of RF Energy applications.1-4 Most noteworthy, are all kinds of industrial heating, drying, curing, sintering or similar processes that are currently being developed with solid-state RF rather than the legacy magnetron as the driving source.
One of the major drivers for the adoption of this technology is the possibility to run consumer microwave ovens from solid-state power amplifiers. The large number of ovens being built with the magnetron every year (in excess of 70 million devices), makes it a very attractive business proposition—provided the system cost, which would seem to rise with current power amplifier cost levels, can be kept in check. Also, customer satisfaction or a great user experience should go without saying with a precision cooking device versus a legacy, reheating unit, which is based on a magnetron.
The system cost is being dealt with within the RF Energy Alliance (RFEA), while how to create a great user experience with microwaves as the energy source is the topic of research within white goods companies— probably more than ever before. With the legacy ‘frequency hopping’ magnetron the systems tried to do their best to deliver energy ‘on average’ to heat things up. Employing a turn table or mode stirrer attempted to improve the performance and increase homogeneity with varying success.
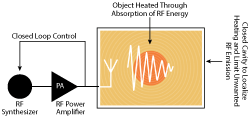
Figure 1 Solid-state powered RF energy application.
Through solid-state technology, the systems are suddenly ‘controlled’. This means that rather than relying on a ‘randomly’ operating source (the magnetron) in conjunction with an averaging device (the turntable), the system controller needs to ‘know’ and ‘predict’ what kind of frequencies, power levels and phase differences the RF signals from various channels need to be in order to achieve the optimal results. To do nothing here (not changing the RF vectors) is not an option! It will make the cooking results worse. Hence, the new technology comes with great promise, but also a lot of work to actually understand how to ‘instill’ into the solid-state cookers the appropriate algorithms (i.e., smartness) to achieve excellent results.
I have discussed the technical challenges associated with the RF generation for solid-state RF heating systems in Microwave Journal before.5 This article discusses basic concepts of applying microwaves to food processing for both industrial and consumer use. The ‘new kid on the block’, solid-state generated and amplified RF is not a new concept but it needs to be rethought in order to make the best of the new possibilities—predominantly control—that comes with solid-state RF generation. In the following paragraphs, a number of the characteristics of the new technology are presented.
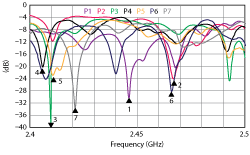
Figure 2 S11 response vs. physical position of the load on a ground plane inside a cavity.
RF energy applications typically make use of an RF-tight cavity, which contains the load to be processed and into which the RF is irradiated by means of antennae (see Figure 1). The application controller is able to determine the exact cavity/load conditions during the process via feedback (VSWR) provided, and can react accordingly.
Solid-state systems are flexible with respect to the number of channels and/or solid-state power amplifiers ‘around’ a processing cavity. This allows power scaling with the number of channels, and the independent (different frequencies per channel) or coherent (same frequency with particular phase offset) RF drive of the process. Together with the multimode cavity (high Q structure), this offers system designers a choice to actively control the electromagnetic field distribution inside, which is the core ingredient to a great cooking result provided the controller knows ‘what to do’.
We clearly need to separate the industrial and consumer oriented system designs: the industrial user can typically rely on a constant or slowly varying load, mostly in continuous flow processes (e.g., along a belt) with high to very high power levels (10 to > 100 kW) in a single system. Controlling the RF power under such circumstances is relatively simple and can safely rely on a very limited number of strategies to achieve adequate energy delivery. Machines typically run a single process such as pasteurization, sintering, ceramic and pharmaceutical drying, etc.
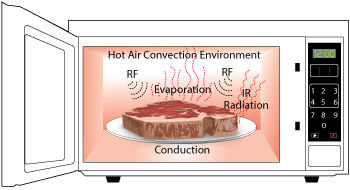
Figure 3 Heat transport mechanisms cooking food.
The consumer oriented cooking ‘processes’ need more sophisticated strategies: defrosting, baking, broiling, simmering, sous-vide, reheating, simultaneous multi-food items, etc. plus the fact that those processes are run in batches rather than as a flow and the drive towards minimized user input (who still knows how to cook?), make it much more difficult to cater for all circumstances. Indeed, the shear fact that the position inside the cavity is ‘free’ already makes a big difference. The electromagnetic conditions can be totally different by just varying the position of load items inside a cavity (see Figure 2 for an example).
COOKING GOAL
Cutting a lot of corners, cooking is about dosing the right amount of energy over time at intended locations outside, and possibly, inside of foodstuff. In the end, this energy delivery gives rise to temperature increase and/or chemical and physical changes of the foodstuff such that we can later enjoy tasty and healthy meals. There are multiple physical processes involved including energy absorption in or at the surface, thermal conduction and convection to transport heat inside foodstuff, heat loss at the surface via radiation and evaporation of liquids, and changes of parameters governing those processes in the course of the cooking (illustrated in Figure 3). Regardless of how the energy for the cooking process is provided, the expectation is that all cooked foodstuff has received the intended energy dose everywhere.
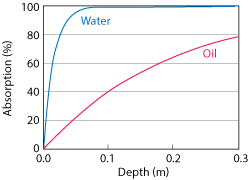
Figure 4 Absorption depth of micro-wave radiation in water and oil.
PHYSICS
Conventional ways to cook usually provide the cooking energy through immersion of the foodstuff into a heated medium (water, oil and hot air) or radiation (infrared). Heating via microwaves belongs to the latter group, but in contrast to the generally limited penetration depths of infrared (IR) radiation (< 5 mm for near IR frequencies > 780 nm in tissue),6 microwaves can penetrate deep (up to cms) into the foodstuff. In the following paragraphs, the relationships governing the energy delivery via microwaves into dielectric loads will be briefly presented.
The equation (which ‘powers’ all microwave heating processes):
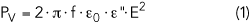
describes the power delivered into a volume element inside matter with a dielectric loss factor ε’’, caused by microwave radiation with an average E-field magnitude E, the frequency f and the vacuum dielectric constant ε0.

Figure 5 Dielectric constant and dielectric loss factor of a dilute salt solution vs. temperature.
A wave traveling inside foodstuff will hence deliver energy according to this equation and gets attenuated along the way. Depending on ε”, this happens more or less quickly and it is helpful to define a ‘penetration depth’ ld, which denotes the distance into the solid when the incoming field strength has diminished by 1/e times the value at the surface. For ε”/ε’ << 1, this ld can be approximated by:7

This allows the calculation of the absorption of the field and hence the energy delivered after some distance x into the medium:7

Figure 48 depicts the absorption depth of 2.45 GHz radiation in water and oil. Clearly, the microwaves penetrate oil much deeper than water.
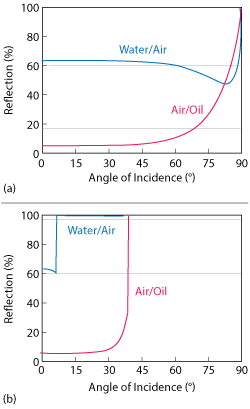
Figure 6 Reflection vs. angle of incidence for unpolarized, 2.45 GHz radiation entering (a) and exiting (b) air/oil and air/water interfaces.
Knowing the specific heat capacity of the material, the expected temperature rise of the specimen for the regions absorbing the electromagnetic energy can be calculated. Interestingly, in this example, the temperature for both water and oil will rise by roughly the same amount due to the lower specific heat of oil, but the oil will heat up more homogeneously throughout the sample, whereas the water will heat up in a relatively smaller absorption region (neglecting conductive and convective heat transfer inside the material).
So far in the discussion, we have assumed that the dielectric constant ε’ and loss factor ε’’ are constants with respect to frequency and temperature, which is not the case. For a rigorous treatment of the subject, this dependence needs to be taken into account. For example, ε’’ of clean water becomes smaller with temperature. The water will absorb microwaves less well at higher temperatures. Salty water exhibits opposite behavior: the loss increases with temperature (qualitatively depicted in Figure 5).9 In real food, this gives rise to ‘thermal runaway’—relatively hot spots inside food will keep increasing in temperature faster than their environment, which leads to pronounced inhomogeneity.
Electromagnetic waves experience reflection and diffraction at interfaces from air to matter and vice versa—exactly similar to these effects in optics, following the same equations. For water and oil interfaces with air, the result can be seen in Figure 6.8 The dielectric constant ε’ of water gives rise to high reflectivity at the air to water interface of about 60 percent for basically all angles of incidence. Interestingly, at the water to air interface (leaving the specimen) the wave will experience total reflection for all angles of incidence but the smallest: microwaves are practically trapped inside water.
MODES
For domestic as well as industrial heating, resonating multi-modal cavities are typically used to apply the electromagnetic field to the load. These resonators together with the permittivity of the load applied ‘allow’ only certain frequencies inside to propagate, which create particular electromagnetic energy distributions, the ‘modes.’ The localized energy distribution associated with a particular mode will only deliver energy to dissipative loads at those spots.
It is clear that in order to have the load absorb the offered energy evenly, a number of complementary modes need to be created inside the cavity, e.g., via frequency variation of the incoming wave. Refer to Figure 7 for an impression on the electrical field distributions of several modes excited by different feeds in an empty rectangular cavity.10,11
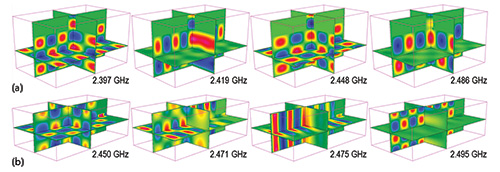
Figure 7 Instantaneous electric fields in the coordinate planes excited by horizontal (a) and vertical (b) feeds in a two-feed empty rectangular cavity.
The clear discernibility of modes or resonances is a typical feature of a more or less empty cavity (Q still ‘high’). With increasing dissipative load, it becomes part of the electrical length of the cavity and the resonance conditions change. In the extreme case of a fully loaded cavity, no mode spectrum exists and the homogeneity becomes a function of penetration depth into the load.
In addition to the modes of the cavity, the shape and dielectric permittivity of loads also play an important role with respect to homogeneous energy deposition in the load. The load geometry, together with internal and external reflection, will create a dielectric resonator with a particular field distribution inside the load, which in turn depends on the outside field distribution. Simulated distributions of dissipated power for various resonant frequencies (at which the loads have much better energy coupling) excited by two different feeds in a particular rectangular cavity are shown in Figure 8.11 The patterns are highly non-uniform, and some of them dominate over others; this is explained by the depths of corresponding resonance: the deeper the resonance, the higher the energy coupling and the values of dissipated power in the pattern.
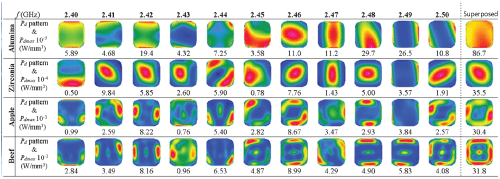
Figure 8 Energy deposition vs. frequency within various 50 mm × 50 mm × 10 mm loads within the same cavity.
To summarize, microwave heating overcomes the thermal diffusion limited energy delivery through the surface to any kind of load through the possibility to penetrate the load and hence directly heat up the volume elements away from the surface. Unfortunately, it is not as straightforward as that, but a number of effects counteract homogeneous energy distribution inside the load:
- Inhomogeneous load/inhomogeneous dielectric (absorption) properties
- Low thermal conductivity of load
- Heat capacity of load
- Loss factor depending on temperature of the load that may change grossly during the process (thawing/defrosting)
- Pronounced edge heating and corner heating
- Energy hotspots due to modes in applicator
- Resonances inside the load
- Evaporation (heat loss) from the surface.
STRATEGIES
As a reminder, the goal of the cooking process was to supply the right amount of energy to any volume element of the load in order to achieve the intended temperature change and temperature setpoint over time.
Going further, three different load scenarios will be identified:12
- Load is basically transparent to microwave radiation; weak absorption
- Absorption depth ≈ load geometry/2
- Absorption depth < load geometry/2
Case 1 is great for homogeneity, but may take high field strengths for effective heating (see Equation 1). 915 MHz radiation is very likely a good choice here above 2.45 GHz. Of course, the frequency can be chosen (if regulatory possible) such that the absorption depth fits better with the sample geometry (see Case 2). Given the low absorption, special care needs to be taken for the RF power measurements (forward power, reflected power). Usually the difference (reflected—forward) would be associated with the ‘delivered’ or ‘absorbed’ power. However, the walls of the apparatus or other elements of the machine may actually absorb power as well and hence the measurement needs to be carefully calibrated to identify other ‘consumers’. Also, under these conditions, some RF power will be reflected back into the generators; special care needs to be taken to stay within the VSWR budget for the amplifiers.
Case 2 appears ideal for microwave based heating processes: the irradiated microwave energy is used efficiently (all the irradiated energy is being absorbed on the first ‘pass’ through the load; access to the load from all sides for the microwave radiation is assumed. Also, for homogeneity, this case does not need to rely on thermal diffusion (see Case 3). To promote homogeneity, several modes with different field distributions should be used. Depending on the exact parameters, edge heating may become an issue. If so, appropriate modes should be used to minimize the artifacts.
Case 3 is probably the most difficult one to get right in terms of homogeneity and process result: All microwave power is absorbed in a relatively (to the total extent of the load) small sub-surface depth. Edge heating is very likely and proper countermeasures need to be taken —the same goes for homogeneity along the surfaces at large. Also, the bulk of the load needs to be heated via the heat flux along the temperature gradient from the surface towards the bulk. If the thermal conductivity is low, the overall process will be slow and the use of microwaves may not actually be the optimal choice to heat the load. It could well be that the surface becomes too hot (thermal diffusion is slow), and/or dries out when water present is evaporated.
INDUSTRIAL VS. RESIDENTIAL APPLICATIONS
It appears that the realization of a perfect cooking/processing apparatus is less tricky from a process perspective in the industrial field. Typically, the loads presented to the systems are well known with respect to geometry, physical and chemical properties, are reproducible, uniform (at least on average) and do not change rapidly with time. Also, additional sensors for temperature, humidity, weight and such are likely to be present and their data used by the process controller. Under such circumstances, a system can be fully optimized for any of the three load scenarios discussed earlier.
The frequency to use (915 MHz or 2.45 GHz) can be chosen based on absorption properties in connection with thermal diffusion speeds, regional spectrum, the power needed, efficiency requirements, etc. The RF control would seek to create as many complementary modes as possible, keep track of the delivered energy to realize intended temperature increases and monitor safety critical parameters. With solid-state generators, the system designer now also has a choice to move away from a limited number of high power microwave sources and to implement a more distributed RF power delivery (e.g., along a conveyor belt), which provides additional redundancy and fine-tuning capabilities to achieve a better process result (higher yield) than with less granular magnetron based systems.
On the other hand, it appears that the realization of a perfectly processing residential cooking system is a much more daunting task. Although the operating frequency is more or less fixed within the 2.45 GHz band (the 915 MHz ISM band is not available throughout the world), there are still plenty of RF system-level choices that can be made: The degrees of freedom here relates to the power level, number of RF channels and the electromagnetic design of the cavity with antenna port locations and overall geometry. One basic problem for residential systems is that the possible loads are basically endless: from hardly any load (or accidental misuse) to large absorptive ‘meals’ with all kinds of compositions (varying permittivity), geometries and weights.
Additional complexity arises with the introduction of additional heat sources like hot air convection, steam or broiling elements, whose respective contribution needs to be taken into account.
CONCLUSION
With all control and reproducibility, the designer has over the parameters of the RF signal, which is used to heat up a food load, comes the responsibility to ‘know what to do’—in former times the magnetron with its stochastic and ageing behavior has taken those decisions. However, ‘knowing what to do best’ is not an easy task and depends strongly on the nature of the heating process, the volumes, shapes, temperature gradients, physical phases, etc. of the foodstuff. One could even argue that things have become more difficult than ever before to get the process right and produce the intended user experience. The industrial world seems to present a comparatively simpler task with well-known, generally homogeneous and uniform loads.
The realization of the perfect cooker for residential applications appears much more complicated in view of the multitude of conceivable loads and load conditions and hence the co-existence of load cases discussed in this article. However, it is clear that with the high degree of control, which is available through solid state RF, this kind of appliance has come within closer reach than ever before.
References
- M. DeVincentis, G. Hollingsworth and R. Gilliard, “Long Life Solid-State RF Powered Light Sources for Projection Display and General Lighting Applications,” Microwave Symposium Digest, IEEE MTT-S IMS, June 2008.
- K. Werner and S. Theeuwen, “RF Driven Plasma Lighting: The Next Revolution in Light Sources,” Microwave Journal, December 2010.
- K. Werner, H. Heuermann and A. Sadeghfam, “The Potential of RF Energy for the Ignition of Microplasmas,” High Frequency Electronics, November 2012.
- J.F. Bakker, M.M. Paulides, A.H. Westra, H. Schippers and G.C. van Rhoon, “Design and Test of 434 MHz Multi-Channel Amplifier System for Targeted Hyperthermia Applicators,” Int. J. Hyperthermia, March 2010.
- K. Werner, “RF Energy Systems: Realizing New Applications,” Microwave Journal, December 2015.
- K. Krishnamurthy, H.K. Khurana, J. Soojin, J. Irudayaraj and A. Demirci, “Infrared Heating in Food Processing: An Overview,” Comprehensive Reviews in Food Science and Food Safety, January 2008.
- M. Mehdizadeh, “Microwave/RF Applicators and Probes for Material Heating, Sensing, and Plasma Generation,” Norwich, N.Y.: William Andrew, 2009.
- Matthias Rother, Über das Konkurrenzverhalten von Dielektrika bei der Mikrowellenerwärmung, Dissertation, Karlsruher Institut für Technologie, Fakultät für Chemieingenieurwesen und Verfahrenstechnik, 2010.
- www1.lsbu.ac.uk/water/microwave_water.html; with permission.
- V.V. Yakovlev, “Frequency Control Over the Heating Patterns in a Solid-State Dual-Source Microwave Oven,” IEEE MTT-S IMS Digest, Phoenix, AZ, May 2015, 978-1-4799-8275-2/15.
- V.V. Yakovlev, Computer Modeling in the Development of Mechanisms of Control Over Microwave Heating in Solid-State Energy Systems, AMPERE Newsletter, Issue 89, pp. 18–21, 2016.
- M. Grüneberg et al., “Mikrowellenerwärmung von Speisefetten und –ölen” Zeitschrift für Lebensmittelwirtschaft 1992.
