
Filters are fundamental building blocks of nearly every modern RF/microwave system, used to eliminate unwanted signals in receiver and transmitter architectures. Until recently, study and research in practical filter design has been largely devoted to topologies in which rejection of stopband frequencies is accomplished by reflecting undesired signals back to the source. Meanwhile, there are many applications in which these reflections produce intermodulation products, gain ripple and other problems in system performance. For example, nonlinear devices such as mixers, multipliers and high-gain amplifiers which respond to out-of-band frequencies are highly sensitive to the reflections caused by conventional filter designs. This becomes especially challenging as filters are often needed near or adjacent to active devices in the signal path to better define bandwidth or suppress unwanted harmonics.
While RF system designers have used several brute-force approaches to manage these adverse effects, such as inserting attenuators or isolation amplifiers around sensitive components, these techniques are known to degrade overall system signal-to-noise ratio (SNR) and dynamic range. Absorption of stopband signals has been achieved by terminating one port of a diplexer (or all but one port of a multiplexer), but this approach is demanding on space requirements and still results in reflections due to mismatch in the transition. Balanced filters with quadrature hybrids at the input and output can also be used to buffer the circuit from reflective elements, but the bandwidth of the filter is then limited by that of the hybrids, which makes this technique unsuitable for broadband applications.
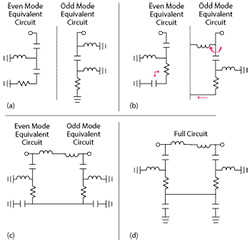
Figure 1 Derivation of a lowpass reflectionless filter topology: even and odd mode equivalent circuits that satisfy Equation 3 (a) re-arranged elements (b) added inactive elements to achieve symmetry (c) and final circuit topology (d).
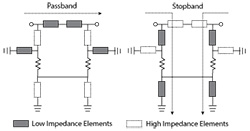
Figure 2 Passband and stopband signal paths through the reflectionless lowpass filter.
Thus, there is a clear need for new filter topologies in RF and microwave systems in which stopband energy is absorbed into the circuit rather than reflected back to the source. This need has led to advanced research and development of a novel, patented topology1 of reflectionless filters, which Mini-Circuits will release to the market for commercial use this year.
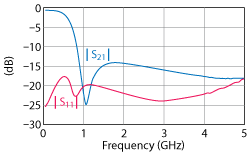
Figure 3 Typical performance of a single pole lowpass reflectionless filter.
Filter Theory and Extensions
The reflectionless filter topology assumes a two-port symmetric network and is derived based on even/odd mode analysis. This approach allows the two-port network to be divided (in theory) into two single-port networks, each of which contains half the elements of the two-port network. In the even mode equivalent circuit, the nodes that lie on the symmetry plane are assigned to an open circuit, while in the odd mode equivalent circuit, nodes that lie on the symmetry plane are assigned to ground (or virtual short). The S-parameters of the two-port symmetrical network are therefore defined as the superposition of the even and odd mode reflection coefficients, such that:
S11 = S22 = 1/2(Γeven+Γodd) and (1)
S21 = S12 = 1/2(Γeven–Γodd) (2)
Given the requirement that the circuit be reflectionless, S11 must be equal to zero (normalized to the characteristic impedance of the network). It follows that:
Γeven=–Γodd (3)
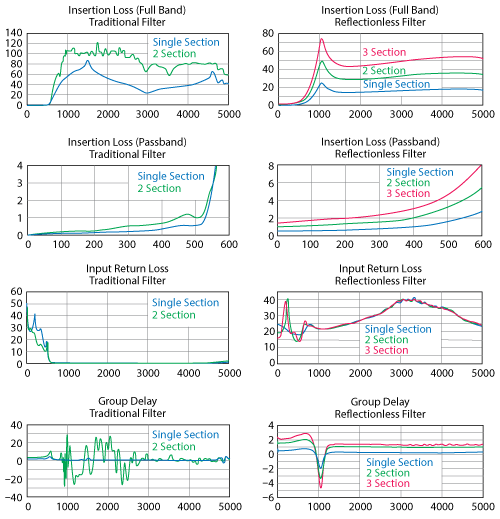
Figure 4 Performance comparison of traditional and reflectionless filters.
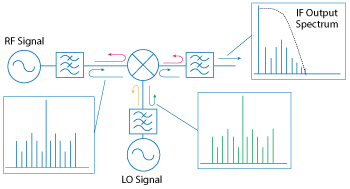
Figure 5 Typical intermodulation expansion due to reflections from multiple filters.
This condition is satisfied when the corresponding elements of the even and odd mode equivalent circuits are duals of one another. The derivation of a reflectionless lowpass filter following this methodology is illustrated in Figure 1.
In the resulting circuit, signals in the filter’s passband travel directly through, from input to output. Signals in the filter’s stopband are routed directly to the resistors, which terminate the signal internally (see Figure 2).2
Figure 3 shows the typical performance of a single pole lowpass reflectionless filter of this class. The filter exhibits a third order inverse Chebychev-type response but is distinct from traditional filters in that the reflection coefficient is zero for all frequencies.3 While this example shows a reflectionless lowpass filter, the same technique has been used to derive a wide variety of highpass, bandpass and bandstop filters.
Extensions of this design approach include higher order filters in which the terminating resistors are replaced with matched sub-networks to achieve improvements in stopband rejection and steepness in the transition. For example, a series of third order lowpass filters (the NRLP3 series) has been developed in which three reflectionless filters are nested, each into the last. These designs exhibit steeper transitions and higher rejection in the first octave of the stopband relative to that of first order lowpass reflectionless filters.
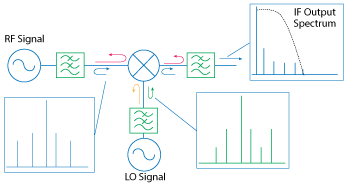
Figure 6 Minimizing the effect of intermodulation expansion by using reflectionless filters on mixer ports.
As another extension, cascading filters are used in many applications to enhance stopband rejection or to combine highpass and lowpass filters to create a bandpass response. While cascading traditional filters can introduce in-band ripple and phase instability, reflectionless filters can be cascaded without adding these effects to the filter’s performance. Figure 4 compares the typical insertion loss, return loss and group delay of a traditional filter to that of a reflectionless filter when cascaded. These curves show that cascading traditional filters creates in-band ripple, degrades return loss and generates phase instability. By contrast, the reflectionless filters exhibit none of these detrimental effects, even when cascaded in three sections.
Practical Applications
Reflectionless filters are particularly useful for pairing with sensitive nonlinear devices, where traditional filters are notoriously problematic. One such case is a filter cascaded with a mixer in the signal chain. Mixers generate spurious mixing products, higher LO harmonics and other unwanted signals that must be filtered out. However, with a conventional filter, these spurious tones are reflected back into the mixer where they can convert again or re-mix with the intended signals to create a multitude of unintended signals that may fall within the desired passband (see Figure 5).
Reducing intermodulation products generated by the nonlinear mixer has always been a design goal, and the industry has had various levels of success with high dynamic range FET based mixers. However, even the best mixers produce intermodulation products at some level from each port which then react with the neighboring elements in the RF chain. When these adjacent elements are filters, the out-of-band intermodulation products are fully reflected back into the mixer to recombine with the fundamental signal and produce additional “family members” of unwanted spurious products. These spurious products make their way to the output IF, and several end up in-band, limiting the overall dynamic range of the system. When out-of-band reflections from filters are minimized, those “family member” spurious products are reduced, resulting in a net reduction of in-band unwanted intermodulation products and improvement in overall system dynamic range (see Figure 6).
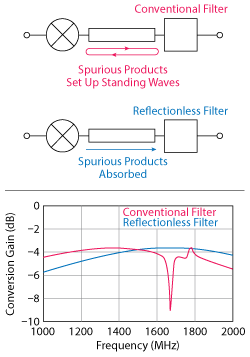
Figure 7 Simulation of a mixer and filter separated by a transmission line, comparing traditional and reflectionless designs.
Additionally, these unwanted spurious products can be substantial in magnitude and of an undetermined phase. Therefore, in certain phase relationships, they can interfere destructively with the down-conversion signal, resulting in a “suck-out” at some point in the frequency band (see the red curve in the response in Figure 7). This occurs commonly in broadband systems, in part because of the greater likelihood of a destructive phase relationship between the reflection and the desired signal over a wide bandwidth. Even in cases where this effect does not occur, the overall shape of the conversion loss curve will change and develop ripples as the electrical length of the line between the mixer and filter changes. In effect, this makes mixer-filter combinations sensitive to environmental conditions as well.
The reflectionless filter, however, causes no such effects to the mixer performance because the spurious mixing products are absorbed, rather than reflected back into the mixer where they can interfere. The conversion loss curve for the mixer in this setup not only lacks the suck-out effect shown by the traditional filter, but is also entirely insensitive to the line length between the filter and the mixer.
These same properties make reflectionless filters suitable for use with other types of sensitive components, such as multiplier chains, where reflections can contribute to unwanted harmonic multiplication and conversion gain ripple. They have also been used to extend the spurious-free dynamic range (SFDR) in analog-to-digital converters (ADC) by absorbing clocked spurs before they can re-enter the ADC. Similarly, they can eliminate unintended feedback in high gain amplifiers and avoid stability problems, without the need for additional attenuators to buffer stopband reflections.
Conclusion
The development of the reflectionless filter topology represents a revolutionary advance that will enable significant improvements in RF system performance in many applications. This technology solves a number of longstanding problems related to embedding filters in transmit and receive chains. Some of the applications which will benefit – or have already – from replacing traditional filters with reflectionless filters have been discussed in this article, but the full scope of their usefulness in practical applications has yet to be realized. Mini-Circuits will release an initial offering of 23 models to the market, featuring first and third order lowpass, highpass and bandpass designs covering passbands from DC to 21 GHz (see Table 1). The filters are fabricated on GaAs using integrated passive device (IPD) process technology and packaged in tiny 3 × 3 mm QFN cases (see Figure 8).
References
Figure 8 NR-series reflectionless filter pinout.
- Protected by U.S. Patent No. 8,392,495 and Chinese Patent No. ZL201080014266.1. Patent applications 14/724976 (U.S.) and PCT/US15/33118 (PCT) pending.
- M. Morgan and T. Boyd, “Theoretical and Experimental Study of a New Class of Reflectionless Filter,” IEEE Transactions on Microwave Theory and Techniques, Vol. 59, No. 5, pp. 1214–1221, May 2011.M. Morgan and T. Boyd, “Reflectionless Filter Structures,” IEEE Transactions on Microwave Theory and Techniques, Vol. 63, No. 4, pp. 1263–1271, April 2015.
Mini-Circuits
Brooklyn, N.Y.
www.minicircuits.com
apps@minicircuits.com

