Starting from a small number of fabricated integrated inductors, and by means of accurate electromagnetic simulations and a physical-based inductor model, a new method to generate an integrated inductor library is reported in this article. The parametric model permits to find the geometric parameters of the inductor that provide the highest quality factor for a particular inductance and frequency of operation. A powerful scalable inductor selection tool (IMODEL) has been developed. This tool has been employed to generate a complete library of inductors integrated on a 0.35 μm SiGe process foundry.
Radio frequency integrated circuits (RFIC), operating in gigahertz bands, require high quality factor integrated inductors at a low cost. The behavior of voltage-controlled oscillators (VCO), low noise amplifiers (LNA), matching networks and distributed amplifiers depends strongly on them. However, low cost silicon technologies use low resistivity substrates that result in important losses and quality factor degradation.
Many foundries offer a set of inductors that the RF designer may employ in their circuits. However, they are not designed for a specific application, so the quality factor may not be as high as the designer needs, or not centered at the required frequency. Alternatively, the inductor may be taken from a complete library, provided that it has been previously built-up. This library must be comprised of inductors for any desired inductance, exhibiting high quality factors at different frequencies and with a minimum occupied area.

Figure 1 Performance comparison between two different 2 nH inductors.
Figure 1 shows an example of the difference between the quality factor of an inductor offered by a SiGe 0.35 μm foundry and a custom designed element. In this case, the designer required a 2 nH inductor to work in the 5 GHz range. Among the inductors available from the foundry, all of them square, the most suitable for the requirements was chosen. It can be seen that the newly designed inductor doubles the quality factor and shifts the maximum peak to the required frequency range.
In this article, a new approach to generate an integrated inductor library is proposed. To accomplish it, a new coil selection tool called IMODEL was developed. By this means, a high-quality inductor library for the 0.35 μm foundry process has been generated.
Methods to Build-up an Integrated Inductor Library
Classical Procedure

Figure 2 Design flow of a traditional procedure to generate an inductor library.
Figure 2 shows the design flow of the typical method to generate an integrated inductor library. The first step in the process is the simulation of a large number of inductors by means of a fast simulator such as ASITIC.1 The time consumed by ASITIC simulations is negligible compared to the time required by an electromagnetic tool. However, numerical simulators provide the inductor performance only for a given frequency, and not the whole behaviour when frequency varies as with an EM simulator.2 In spite of this, ASITIC is employed to select the group of coils that will make up the library.
The next step of the approach is laying out the whole library. Afterwards, it is necessary to measure and characterize the fabricated inductors in order to obtain the S-parameters. Finally, the inductor measurement information may be organized as a database and a tool to assist the designer to select the appropriate device for the required inductance and frequency values can be developed.3
This is a reliable and robust method to generate an inductor library because it is based on actual measurements. Therefore, the designer knows exactly the performance of the inductor chosen for their circuit. However, this approach is very time consuming and increases the overall cost since a huge number of coils should be fabricated and measured to generate a wide and diverse library.
On the other hand, the method does not assure the best inductor for a specific application, since it provides only the most suitable among the library coils. Therefore, it is necessary to develop a fast and cheap approach to assure the optimum inductor for the required inductance and frequency.
New Procedure

Figure 3 Design flow of the new method to generate an inductor library.
Figure 3 shows the design flow of the proposed method. It is based on the fabrication and measurement of a few integrated inductors. Hence, the final cost in time and silicon area is reduced.
On one side, the parametric model proposed previously4 is employed to develop an algorithm to define the geometry of the best inductors for the different inductance and frequency values. If this based-on-physics model is considered accurate enough, an inductor selection tool could be developed.
However, EM simulations are considered more reliable. Hence, the parametric model can be used to generate a list of inductors that will be simulated with the EM simulator to corroborate the model estimations. An inductor selection tool based on the simulations will then be developed.
In this case, the measured results are used to set up correctly an electromagnetic simulator. Momentum©,5 a 2.5D-EM simulator based on the method of moments,6 was employed. Although it does not consider the entire phenomena that occur in an inductor as a 3D tool does,7 Momentum is faster and a very good solution in this case.

Table 1 Test Inductor Geometric Parameters
Nevertheless, getting precise results from a general purpose EM simulator is not a simple task. The substrate and metallization layers provided by the technology should be carefully defined, and the simulator has to be adequately configured, so as to fit measured and simulated results. For this purpose the measurements of 10 octagonal inductors fabricated in the 0.35 μm SiGe foundry process have been employed. The test inductor geometries are summarized in Table 1, where rext is the inductor external radius, w the metal width and n the number of turns. The spacing between metal tracks of different turns, s, is fixed to the minimum allowed by the technology in order to minimize the occupied area and maximize the inductance value.
The measurement system used for the inductor characterization consists of the HP8720ES vector network analyzer and the Summit 9000 probe station. To calibrate the measurement system, the short-open-load-through (SOLT) method was applied. Finally, a four-step de-embedding method8 was followed to remove the parasitic effects introduced by the measurement structures.
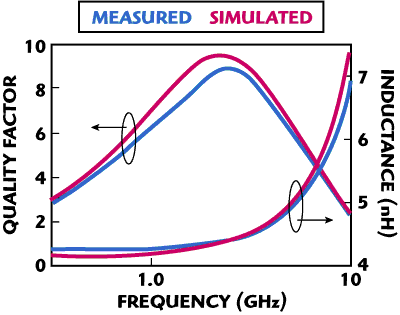
Figure 4 Measured and simulated results for one of the fabricated inductors.
By using the inductor measurements, Momentum was set up correctly, achieving relative errors less than 5 and 10 percent for the inductance value and the maximum quality factor, respectively. As an example, Figure 4 shows the measured and simulated data for one of the fabricated inductors with rext= 90 μm, w= 6 μm and n= 4.5. It is worth noting, however, that the relative errors increase for inductors where skin effect or eddy currents are particularly significant.9
IMODEL
The analytical model4 was validated to be applicable over a wide range of octagonal inductor geometries fabricated on the SiGe 0.35 μm process. The model shows excellent agreement with measurements, and the generated relative errors are similar to those given by the EM simulator. Since building up an inductor database based on EM simulations is a more time-consuming task, the inductor selection tool proposed in this study is based on the parametric model.
The set of equations the model consists of have been implemented by an optimization algorithm that provides the geometry of the inductor with the best quality factor for a given inductance value and frequency of operation. For this purpose, a sweep for the different inductor geometrical parameters is run. The algorithm can be summarized in the following steps:
- The user determines the required inductance value and the frequency of operation. In addition, the allowed tolerance in the inductance calculation must be set up.
- Once the input data has been established, the algorithm searches the coils with the required inductance by sweeping the values of w, rext and n. As mentioned before, s is fixed to the minimum allowed by the foundry process in order to maximize the inductance value per area.
- Each set of w, rext and n that provides the required inductance is saved in a database together with the inductance and quality factor values at the required frequency.
- Finally, the algorithm chooses among the inductors of the database the one with the highest quality factor, which will be the output of the procedure.

Figure 5 Main menu window of the inductor selection tool IMODEL.
This algorithm, together with other functions, has been implemented in MATLAB to compose an inductor selection tool called IMODEL. Figure 5 shows the tool main menu window. Apart from the selection of the best inductor for a required inductance and frequency, the software offers other useful features:
- Provides the two-port π-equivalent model of an inductor from the geometrical parameters rext, w, s and n.
- Generates a text file with the characteristics of all the inductors that provide the inductance and frequency requirements.
- The option “Number of metal levels” allows running a search among two-metal level inductors, which are a better choice in some cases.
- Visualizes the quality factor and inductance plots for a given inductor.
- Visualizes, through 2D and 3D plots, the dependence of the quality factor and inductance on the geometrical parameters for all the inductors that satisfy the input requirements. As an example, Figure 6 shows a three-dimensional plot of the quality factor dependency on w and n of 3 nH inductors at 3 GHz. It is observed that the best inductor performance is obtained for track widths from 6 to 15 μm and number of turns from 3 to 7.

Figure 6 Example of a three-dimensional plot generated by IMODEL.
The tool is scalable and applicable to any foundry process, provided that the parametric model predicts the performance of the inductor correctly. By choosing the option “PARAMETERS” in the main menu, the user can modify the process parameters that are required for the search (see Figure 7). Finally, the tool provides on-line help and a user’s manual to explain the different software features and the error messages that the designer could find when employing the software.

Figure 7 Modification of the process parameters.
Integrated Inductor Library
By using the coil selection tool IMODEL, a library of inductors integrated on the 0.35 μm process has been generated. The coils have been generated for the frequencies 0.85, 1.5, 1.8, 2.4 and 5.6 GHz, corresponding to different known standards. Each set offers inductance values from 0.5 to 6.5 nH, in 0.5 nH steps. The maximum error on the inductance value for the parametric model has been set to 0.2 nH.
As explained before, the algorithm searches the coils with the required inductance by sweeping the geometrical parameters. In this case, the limits for this sweep have been set according to empirical criteria in order to avoid too large inductors and model applicability.7,10,11
The covered range in the search is given by:
- External radius (rext): between 25 and 200 μm
- Number of turns (n): between 1.5 and 10.5
- Track width (w): between 5 and 30 μm
- External to internal radius ratio (rext /rint): lower than 3

Table 2 Main Parameters of the Library Inductors
Table 2 summarizes the main parameters obtained for each set of inductors (from 0.5 to 6.5 nH) of each frequency. As it can be seen, the higher the operation frequency is, the lower the rext values (rmin and rmax) and w values (wmin and wmax) become. This is associated to the decrease of the parasitic capacitance when the external radius or the metal width decreases. Therefore, the resonant frequency becomes higher, and the quality factor peak is given at a higher frequency.

Table 3 Main Parameters of the Two-Metal Level Inductors at 0.85 GHz
At the lowest frequency of the library (0.85 GHz), the average quality factor is lower and the occupied areas are larger than the rest. It is well-known that the quality factor increases when other layers are added to the metallization structure due to the decrease of the final conductor resistance.12 However, the inductance value is hardly changed by shunting another metal level. According to this consideration, an additional set of inductors has been developed by using the two metal layers option offered by IMODEL at 0.85 GHz. The new parameters obtained by designing two-metal level inductors at 0.85 GHz are summarized in Table 3. The average quality factor is now higher, and the maximum external radius is slightly lower, which saves silicon area.
Conclusion
In this article, a new method to generate a full inductor library has been introduced. From a few fabricated inductors in a given technology, the EM simulator Momentum is configured accurately to provide consistent results. On the other hand, a parametric model is developed. If this model is not accurate enough, it will be used to generate a list of optimal inductors. These coils will be simulated to obtain more reliable data, and the results will be organized to develop an optimal inductor selection tool based on simulations. Alternatively, if the physical-based model predicts the coil behaviour correctly, the inductor selector will be based on it.
In this work, a high quality factor searching tool named IMODEL has been developed based on a parametric model. By means of this useful software, the RF designer can obtain in a fast and reliable way the best inductor for a required inductance value and working frequency. Based on this powerful tool, a wide inductor library has been developed consisting of high performance coils integrated on a 0.35 μm SiGe foundry process.
Readers interested in the program can obtain a free executable file by writing to Dr. Amaya Goñi, Instituto Universario de Microelectronica Aplicada, Universidad de Las Palmas de Gran Canaria, 35017 Las Palmas de Gran Canaria, Spain.
Acknowledgments
This work has been partially supported by the Spanish MEC and MITyC under projects TEC-2005-08091-C03-02, TEC-2005-06784-C02-02 and FIT-330100-2006-43.
References
1. A. Niknejad and R.G. Meyer, “Analysis, Design and Optimization of Spiral Inductors and Transformers for Si RF ICs,” IEEE Journal of Solid-State Circuits, Vol. 33, No. 10, October 1998, pp. 1470-1480.
2. I.D. Robertson and S. Lucyszyn, “RFIC and MMIC Design and Technology,” IEEE Proceedings on Circuits, Devices and Systems, Vol. 13, 2001, pp. 154-171.
3. J. Pino, J.R. Sendra, A Hernández, S.L. Khemchandani, J. Aguilera, B. González, J. García and A. Nunez, “Models and Tools for CMOS Integrated Inductors,” Analog Integrated Circuits and Signal Processing, Vol. 33, 2002, pp. 171-178.
4. A. Goñi, J. del Pino, B. González and A. Hernández, “An Analytical Model of Electric Substrate Losses for Planar Spiral Inductors on Silicon,” IEEE Transactions on Electron Devices, Vol. 54, No. 3, March 2007, pp. 546-553.
5. http://eesof.tm.agilent.com.
6. R.F. Harrington, Field Computation by Moment Methods, IEEE Press, New York, NY, 1993.
7. J. Craninckx and M.S.J. Steyaert, “A 1.8 GHz Low Phase Noise CMOS VCO Using Optimized Hollow Spiral Inductors,” IEEE Journal of Solid-State Circuits, Vol. 32, No. 5, May 1997, pp. 736-744.
8. T.E. Kolding, “A Four-step Method for De-embedding Gigahertz On-wafer CMOS Measurements,” IEEE Transactions on Electron Devices, Vol. 47, No. 4, April 2000, pp. 734-740.
9. A. Goñi, J. del Pino, B. González, S. Khemchandani and A. Hernández, “Accurate Planar Spiral Inductor Simulations with a 2.5-D Electromagnetic Simulator,” International Journal of RF and Microwave CAE (under review).
10. N.A. Talwalkar, C.P. Yue and S.S. Wong, “Analysis and Synthesis of On-chip Spiral Inductors,” IEEE Transactions on Electron Devices, Vol. 52, No. 2, February 2005, pp. 176-182.
11. I. Cendoya, N. Sainz, J. Mendizabal, R. Berenguer, U. Alvarado and A. García-Alonso, “Study of the Proximity Effect in High Q Inductors with CMOS 0.18 µm Technology,” XIX Conference on Design of Circuits and Integrated Systems Digest, 2004, pp. 524-527.
12. J.N. Burghartz, “Spiral Inductors on Silicon—Status and Trends,” International Journal of RF and Microwave CAE, Vol. 8, 1998, pp. 422-432.
Amaya Goñi received her MS degree in telecommunication engineering from the Public University of Navarra, Spain, in 2002, and her PhD degree in 2002 from the University of Las Palmas de Gran Canaria (ULPGC). Since 2002, she has been with the Institute for Applied Microelectronics (IUMA), involved in the Microlectronic Technology Division (TME) of the University of Las Palmas de Gran Canaria. Her current research interests include high-frequency integrated circuits for telecommunications, with particular attention to the design, characterization and modeling of silicon integrated inductors.
Javier del Pino received his BS and MS degrees in telecommunication engineering and his PhD degree from the University of Las Palmas de Gran Canaria, Spain, in 1996, 1997 and 2003, respectively. Since 1994, he has been with the Microelectronic Technologic Division of the Institute for Applied Microelectronics (IUMA) at the University of Las Palmas de Gran Canaria. In 1998 he joined the University of Las Palmas de Gran Canaria, where he has been an associate professor from 1998 to 2005 and a professor since 2005. Between 2000 and 2002, he was an invited researcher in the Centro de Estudios e Investigaciones Técnicas de Guipúzcoa, Spain, and in the Fraunhofer Institute for Integrated Circuits, Germany, respectively. His research interests include high-frequency integrated circuits for telecommunications, with particular attention to the design, characterization and modeling of silicon integrated inductors.
Octavio Medina Day received his MS degree in telecommunication engineering from the University of Las Palmas de Gran Canaria in 2005. From 2003 to 2005 he was in the Research Institute for Applied Microelectronics at the University of Las Palmas de Gran Canaria. His research work involved integrated inductor modeling using electromagnetic simulators. He is currently working in the UK for a software company.
Sunil Lalchand Khemchandani received his MS degree in telecommunication engineering in 2000 and his PhD degree in 2007, both from the University of Las Palmas de Gran Canaria. In 1998 he joined the Research Institute for Applied Microelectronics of the University of Las Palmas de Gran Canaria. His research work involved GaAs ICs for video and image processing. From 2001 to 2003, he worked for INCIDE, where he was involved in the modeling of inductors in CMOS technology, designing LNAs for GPS applications, transimpedance amplifiers for SONET/SDH and PLLs for MMDS application. His research interests include high-frequency integrated circuits for telecommunications, with particular attention to the design of VCOs, LNAs and mixers in CMOS technology.
Antonio Hernández received his PhD in telecommunication engineering in 1992 from the University of Las Palmas de Gran Canaria, Spain. He is the founder member of the Institute for Applied Microelectronics (IUMA) of the University of Las Palmas de Gran Canaria, where he is a professor. His current research interests include modeling of active and passive devices for microwave and very high-speed applications and RF integrated circuits.
