Automated testing of MMICs often uses wide electrical specifications that, unfortunately, allow outliers into the pass population. Although removal of these outliers has been extensively studied in recent years, most of this work is intended for post processing and not for the test floor. This article describes an adaptive, real-time algorithm for identifying MMIC outliers during automated testing and demonstrates its use on the test floor. Principal component analysis transforms the multivariate data into a score matrix, then a new n-dimensional ellipsoid criterion is applied to capture the outliers. The quality of outlier removal across multiple product families is demonstrated.
Large scale testing of integrated circuits often uses wide, univariate electrical specifications to eliminate defective parts. Although this approach is designed to maintain a high yield, it fails to identify the outliers, either the components that pass the electrical specifications but differ from the normal population, or components that have an abnormal combination of univariate measurements. The process of identifying and removing these outliers is essential to ensuring the consistency and quality of the product.
As a result, various methods have been developed that use a multivariate approach to outlier removal. For example, O’Neill1 and Sharma et al.2 use principal component analysis (PCA) to reduce multi-dimensional data to a single univariate result, then apply a test statistic as the outlier detection. Similarly, Nahar et al.3 perform PCA, calculate a Euclidean distance for the transformed variables and use statistics based on the cumulative distribution function to determine outliers. Banthia et al.4 also perform PCA, then identify outliers using a clustering algorithm. Jauhri et al.5 and Stratigopoulos6 use machine learning to detect outliers, though both describe initial outlier screens that are not sufficient for final testing. Finally, Yilmaz et al.7 describe a multivariate kernel-based method that is intended to be placed in the test flow but appears never to have been applied on the test floor. These methods are not easily applied to real-time measurement systems. A summary of these works is listed in Table 1.
Table 1: Comparison of Outlier Removal Methods
|
Reference |
Multivariate? |
Final Test? |
Real Time? |
On Test Floor? |
|
1 |
YES |
YES |
No |
No |
|
2 |
YES |
YES |
No |
No |
|
3 |
YES |
YES |
No |
No |
|
4 |
YES |
YES |
No |
No |
|
5 |
YES |
No |
No |
No |
|
6 |
YES |
No |
No |
No |
|
7 |
YES |
YES |
YES? |
No |
|
This Work |
YES |
YES |
YES |
YES |
An automated, real-time measurement system (see Figure 1) is typical for large scale testing of packaged MMIC components. The system uses a computer-controlled handler to pick and plunge the device under test (DUT) into a test fixture, perform a series of electrical tests and then place passing DUTs into a tape-and-reel system before selecting the next unit and repeating the test. DUTs that fail are placed in a separate bin. Since the test flow involves the direct transfer of passing units from the test fixture into tape-and-reel packaging, post processing cannot be used to remove outliers, for such an effort would ruin the integrity of the reel. A different approach is required.

Fig. 1 Automated, real-time measurement system. DUTs are plunged into a test fixture, measurements are taken and passing parts are transferred directly onto tape-and-reel.
This article describes a real-time outlier removal method using PCA, which has been implemented on the test floor. The algorithm is deployed over multiple product types operating in the GHz frequency range including driver amplifiers, low noise amplifiers (LNAs), switches and mixers and can adapt to measurement drift over time.
Principal Component Analysis
PCA is a mathematical technique that transforms multivariate, correlated data into uncorrelated, orthogonal variables through projection. The resulting orthogonal variables, called principal components (PCs), quantify the natural variation present in the original data and are ordered such that the first PC describes the most variation, the second PC describes the second most variation, etc. Thus, by defining normal variation, a PCA transformation allows abnormal, outlying data to be identified and removed.1,8
Generally, this transformation begins with an m x n data matrix S, consisting of m observations of n measured parameters. For our purposes, the n parameters are the significant measurements taken during testing (such as DC supply current, gain and noise figure for a low noise amplifier) and each observation, m, is DUT. Since the measured parameters carry different units and magnitudes, the first step in PCA is to normalize the data S into a new matrix X as shown in Equation (1):
where i and j are the row and column matrix indices (i = 1, 2, …, m, and j = 1, 2, …, n), SJ is the column wise mean, and σJ is the column wise standard deviation.
The resulting matrix X has columns each with a zero mean and a standard deviation of one. Next, the covariance of X is calculated via Equation (2):
The eigenvectors (n x n) and the eigenvalues (1 x n) of X* are found, and the column eigenvectors sorted in order of decreasing eigenvalue to form Y, which is referred to as the coefficient matrix. Finally, Z scores (also referred to as PC scores) are produced through the simple matrix multiplication shown in Equation (3):
Here, Z is identical in size to the original data matrix S, but instead of n measured parameters, it contains n PC scores for m observations. The elements of Z are the values that quantify a DUT’s variation from the normal population. Specifically, the further a DUT’s scores are from zero (where “further” is a relative term that varies for each of the n scores), the more likely the DUT is an outlier. For reference, Table 2 summarizes the variables defined throughout this transformation.9
Table 2: Variable Summary
|
Symbol |
Description |
Matrix Size |
|
m |
Number of DUTs |
- |
|
n |
Number of measured parameters per device |
- |
|
S |
Original set of measured data |
m x n |
|
SJ |
Mean of column j |
- |
|
σJ |
Standard deviation of column j |
- |
|
X |
Normalized set of measured data |
m x n |
|
X* |
Covariance matrix of X |
m x n |
|
Y |
Coefficient matrix (ranked eigenvectors) |
n x n |
|
Z |
PC score matrix |
m x n |
Real-Time Outlier Removal Algorithm
Conventional PCA, as described in the previous section, requires the entire set of measurements to be completed before the mathematical transformation can generate the Z scores. However, our test process requires a real-time elimination of outliers since units cannot be removed from tape-and-reel once placed in a socket. Therefore, we developed the real-time PCA algorithm (see Figure 2) that uses predetermined coefficient matrices and outlier criteria.
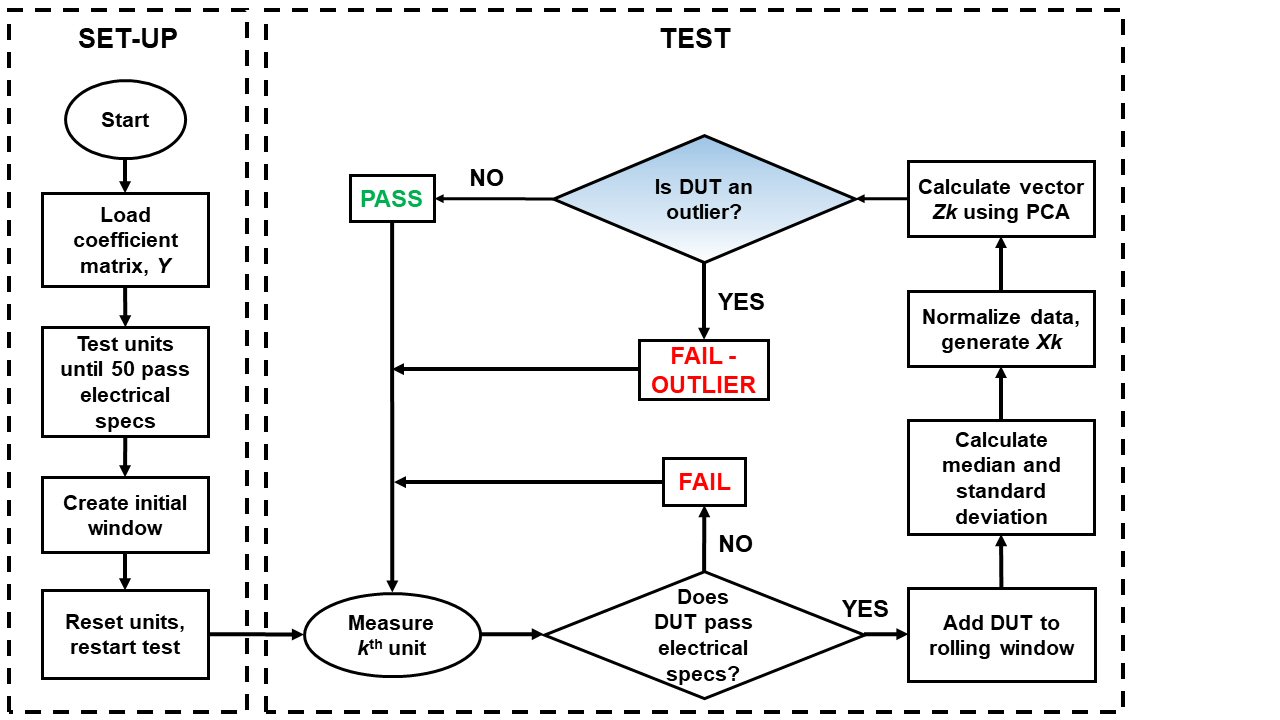
Fig. 2 Real-time PCA algorithm flow chart.
SET-UP Phase
The algorithm begins with the SET-UP phase, shown in the left-hand column. This phase is performed once, before testing a new lot, and begins with the loading of the coefficient matrix, Y. According to conventional PCA theory, the entire lot of data, S, must be processed before the coefficient matrix, Y, can be determined. As an alternative, a predetermined coefficient matrix is loaded that corresponds to the specific product being tested and is generated beforehand using previously measured data from tens of thousands of devices across multiple lots.
Figure 3 demonstrates the approach for one specific LNA with n = 3 measured parameters. Each line in the figure represents the absolute value of element Yi,j in the coefficient matrix Y as more data is added to the calculation. Note that the values of Yi,j generally level off as more data is included, suggesting a common matrix Y for all lots of that specific product. Using this predetermined coefficient matrix eliminates the need to test the entire lot before outliers can be identified and therefore is the basis for the transition to real-time outlier removal.
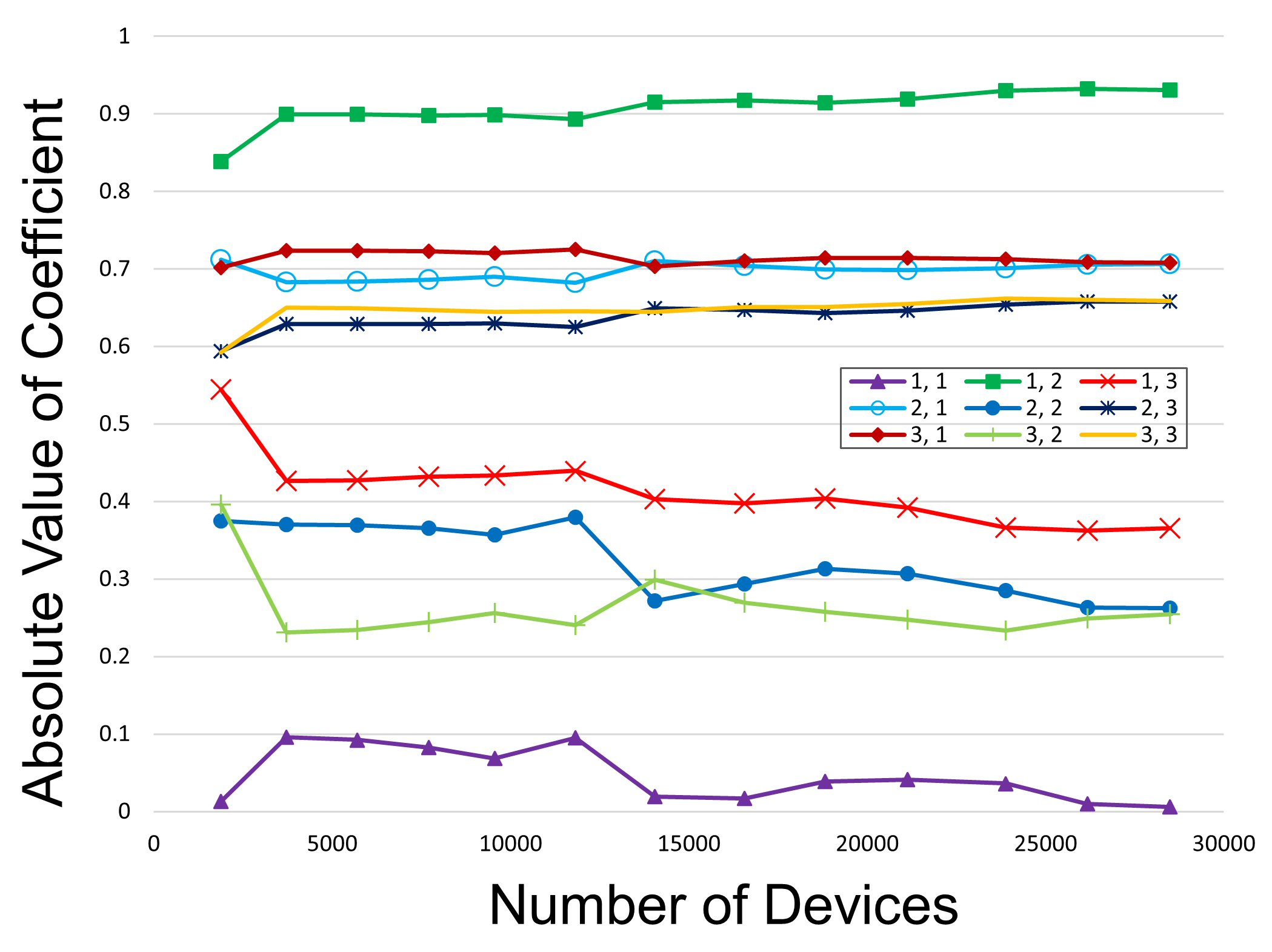
Fig. 3 Absolute value of element Yi,j in the coefficient matrix Y for an LNA as more data is added to the calculation. The legend indicates the specific location (row, column) in the 3x3 matrix.
The next step in the SET-UP phase is to run the test until 50 DUTs pass initial electrical specifications, a number chosen to provide reasonable statistics while not delaying the start of the TEST phase.9,10 Once complete, this set of measurements is used to calculate an initial median and standard deviation for use in the TEST phase. The 50 devices are then returned to untested lot. At this point the SET-UP phase is complete.
TEST Phase
The TEST phase, which is repeated, begins with the measurement of the kth device to generate the data vector Sk. This vector is compared to the electrical specifications of the product. If the DUT fails, it is immediately removed from the population, and we move on to the next device. If the DUT passes, however, its vector Sk is added to the rolling window such that its measurements, along with the 49 previous measurements, are used to recalculate the median and standard deviation. This rolling window allows the algorithm to adapt to measurement drift and other mechanical factors that can skew data throughout the testing of a lot. As mentioned, previously, the size of the rolling window has been previously studied.9,10
Next, the data vector Sk is normalized using the updated statistics. The resulting vector, Xk, is then multiplied by the coefficient matrix Y to generate Zk. The contents of the vector Zk are the n PC scores that quantify the variation of the kth device. Note that despite being generated from data that may be skewed or affected by drift, the values of Zk are normally distributed.8
To demonstrate, consider a lot of approximately 2000 LNAs is tested via the algorithm in Figure 2. This LNA has n = 3 measured parameters: bias current (IDD), gain and noise figure. Figure 4 is a histogram for each measured parameter and Figure 5 shows histograms of the Z scores generated in real-time during testing. For each histogram a curve is displayed that represents a theoretical normal distribution based on the mean and standard deviation of the data.
Note that while the raw measured data in Figure 4 is noticeably skewed with respect to a normal distribution, the transformed distribution in Figure 5 is nearly ideal. This is a desired property of the PCA transformation because it allows predetermination of an outlier criterion that will hold from lot to lot, regardless of drift or skew.
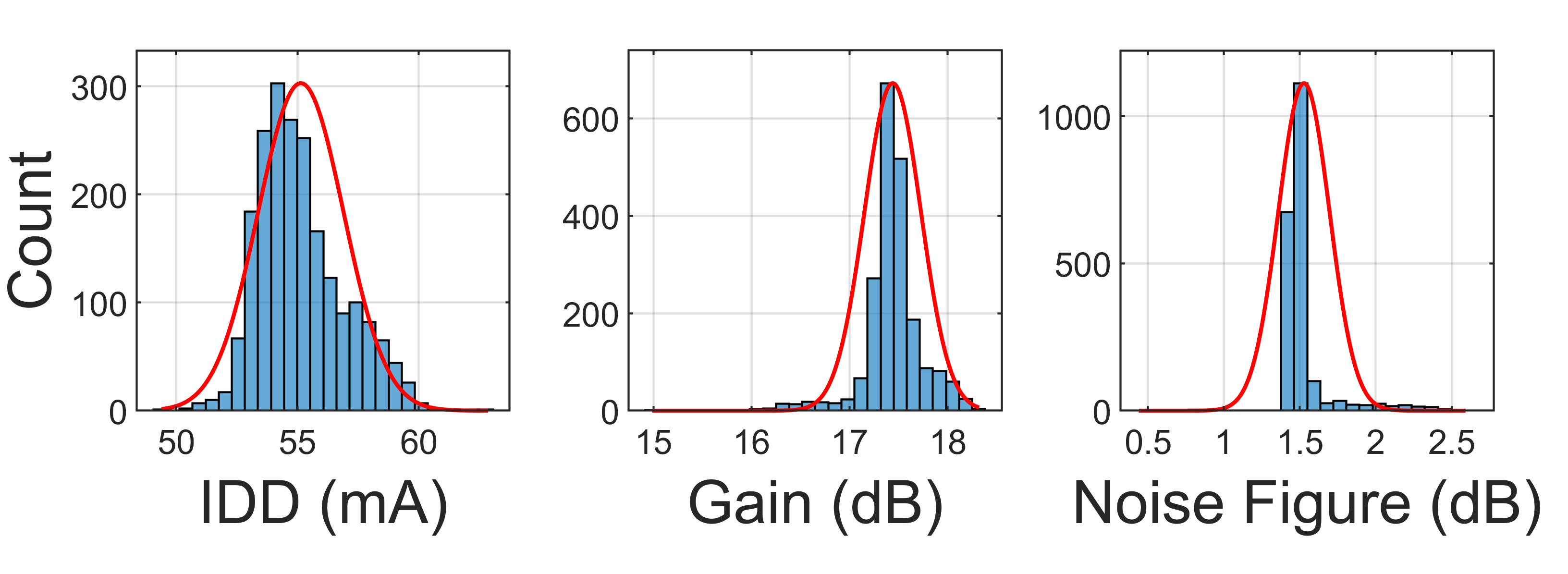
Fig. 4 Histograms (blue) of measured parameters and curves (red) representing a theoretical normal distribution for n=3 measured parameters of one lot of LNAs.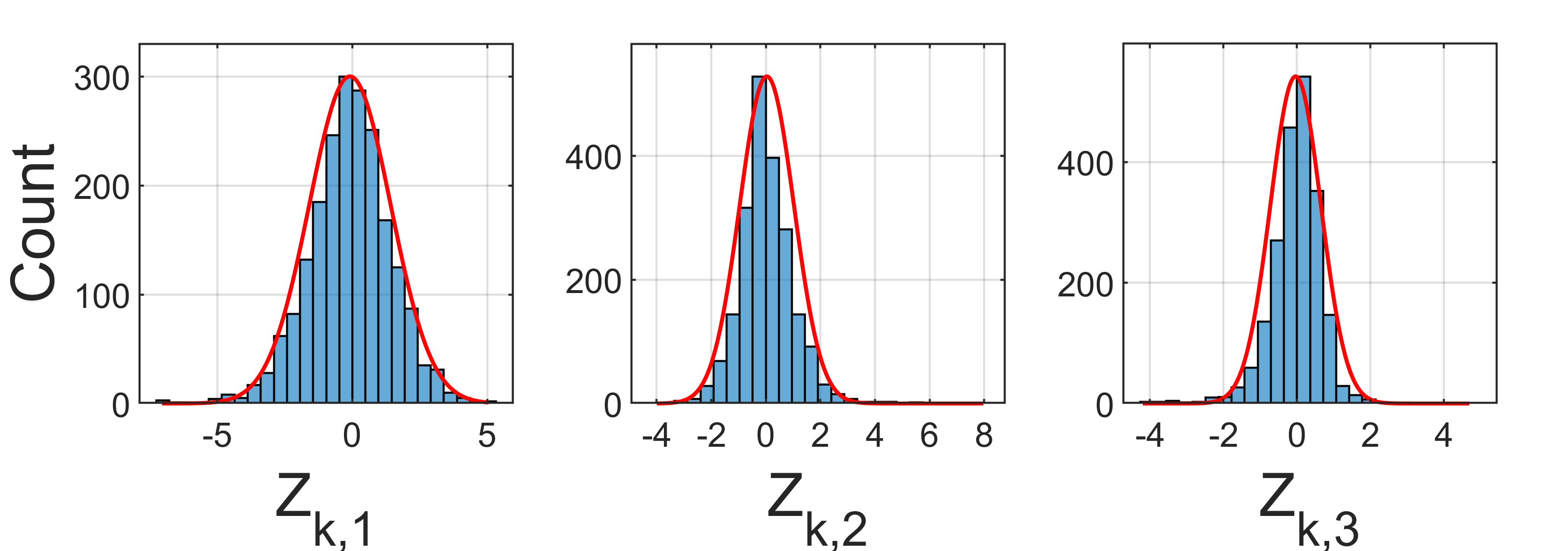
Fig. 5 Histograms (blue) of measured Z scores for the lot of LNAs shown in Figure 3. A theoretical normal distribution is added in red.
The last step in the TEST phase of the algorithm, discussed next, is to process the Zk scores and determine if the kth device is an outlier.
Defining the Outlier Criteria
The criteria for determining an outlier based on the measured Zk scores is a major component of the algorithm described in Figure 2. Initial work9,10 used a single-score decision method, meaning if any of the Zk, scores in absolute value was above a certain threshold, the device was considered an outlier and removed from the PASS population. Threshold values were determined experimentally for each part type (LNA, mixer, driver amplifier, and switch) by considering numerous lots of previous measurements totaling tens of thousands of units. Threshold values ranged from 4.0 to 5.0.
After deploying this single threshold decision method on the test floor for over a year and examining the results, we discovered two shortcomings: 1) too many obvious outliers remained in the PASS population, and 2) too many false outliers were removed from the PASS population.
As an example, consider the results in Figure 6. Real-time test measurements are shown versus unit number for an LNA with n = 3 tested parameters: supply current (IDD, in mA), gain (dB) and noise figure (dB). Every circle represents a unit that passed electrical specifications, with blue circles signifying a PASS unit and red circles signifying an outlier as identified by the single threshold method with a cutoff threshold of 4.0.
In this figure, note that there are four outliers with current greater than 70 mA that were missed by the decision threshold. More importantly, there were too many false outliers identified, especially around unit number 2000, where the measured parameters all appear to be quite consistent. Most of these units should have remained in the PASS population.
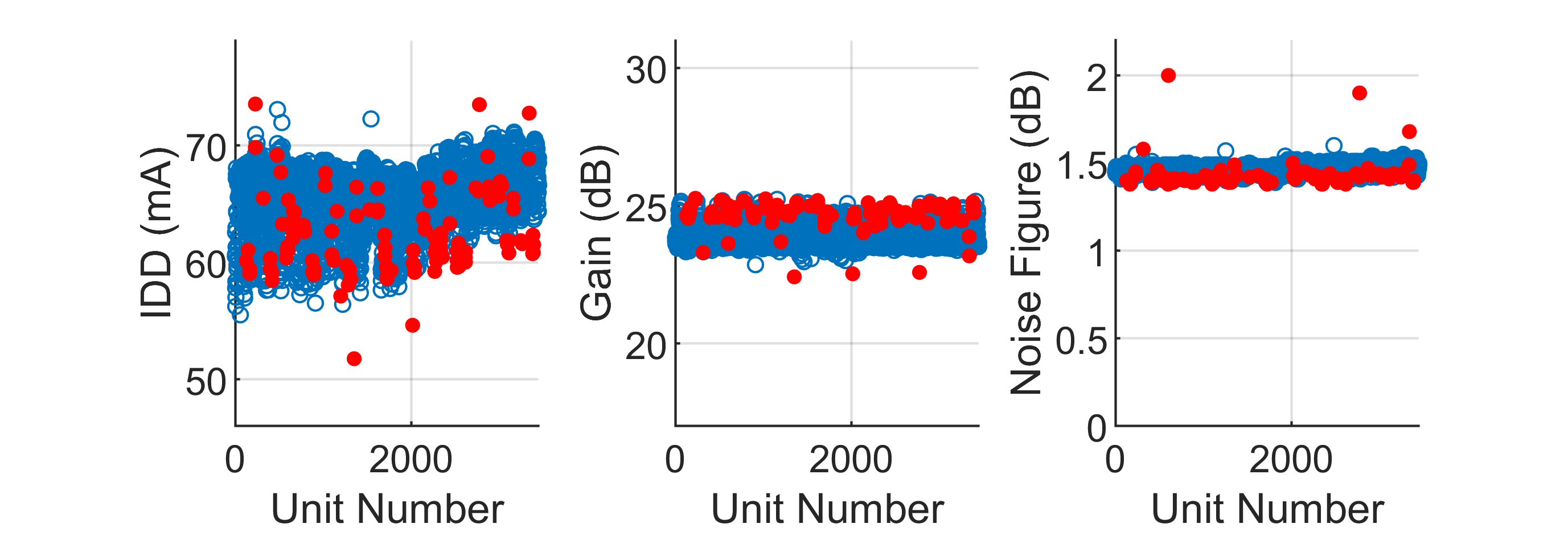
Fig. 6 Real-time measurements for one lot of amplifiers (approximately 2,500 units) showing outliers in the PASS population and false outliers removed from the PASS population. Outliers with a Z score above 4.0 are identified with closed red circles.
Similar results were found over numerous product types, and while the overall outlier removal was low (typically 0.5 to 2 percent of the PASS unites per lot), the single-score decision method was clearly suboptimal. Indeed, this method treats all n of the Zk scores as equally significant, which from PCA theory we know not to be true; the lower order Z scores quantify the variance stronger than higher order ones. As a result, a new outlier decision criterion is proposed that weights the Z scores in an n-dimensional ellipsoid, as shown in Equation (4):
Zk,1, Zk,2,..., Zk,n are real-time PC scores for the kth unit (n total scores per unit), and A1, A2,... An are the axes lengths of the ellipse that defines our cutoff threshold. If a unit generates a set of Zk scores that falls outside of this ellipse, that unit is considered an outlier and removed from the PASS population.
To determine the values of A1, A2,... An for each specific product, the mean is computed plus three standard deviations of real-time Z scores from tens of thousands of previously tested units. The values (which are rounded) are then verified through simulation. Table 3 lists a few examples of the axis lengths derived by this method for several different packaged MMIC components. Note that the axes decrease in length for the higher order Z scores, which corresponds to the relative importance of the various PCs.
Table 3: Summary of Axes Lengths, A
|
Product Type |
Number of measured parameters, n |
A1 |
A2 |
A3 |
A4 |
|
LNA1 |
3 |
5 |
4.5 |
4 |
|
|
LNA2 |
3 |
5 |
4 |
3 |
|
|
DRIVER1 |
3 |
5 |
4.5 |
4 |
|
|
DRIVER2 |
4 |
6 |
5.5 |
5 |
4.5 |
|
SWITCH1 |
4 |
6.5 |
6 |
5.5 |
5 |
|
MIXER1 |
3 |
6 |
5.5 |
5 |
|
The basis for Equation (4) is the statistical tool known as a confidence ellipse.11 Used to evaluate a dataset with normally distributed variables, a confidence ellipse gives a probability that a measurement falls within an expected range. As shown in Figures 3 and 4, while the measured data is generally not normally distributed, the real-time scores show a strong normal distribution. Therefore, Equation (4) can be thought of as a pseudo-confidence ellipse around the Z scores.
As an example, consider Figure 7. Zk,1 and Zk,2 scores are plotted for a lot of LNA1 (approximately 3500 units), with each circle representing a device. Using cutoff axes lengths of A1 = 5 and A2 = 4.5, a cutoff ellipse is generated, which is shown in the dashed line. Also shown is a 99.9 percent confidence ellipse (solid line) based on the set of Zk scores.
The confidence ellipse is very similar in shape and form to the cutoff ellipse, although the cutoff ellipse is slightly larger to account for the inherent tilt of the confidence ellipse. Similar results are observed across several different lots and products, where the cutoff ellipse and confidence ellipse are very similar, thereby confirming the dimensions of our ellipsoidal criterion.
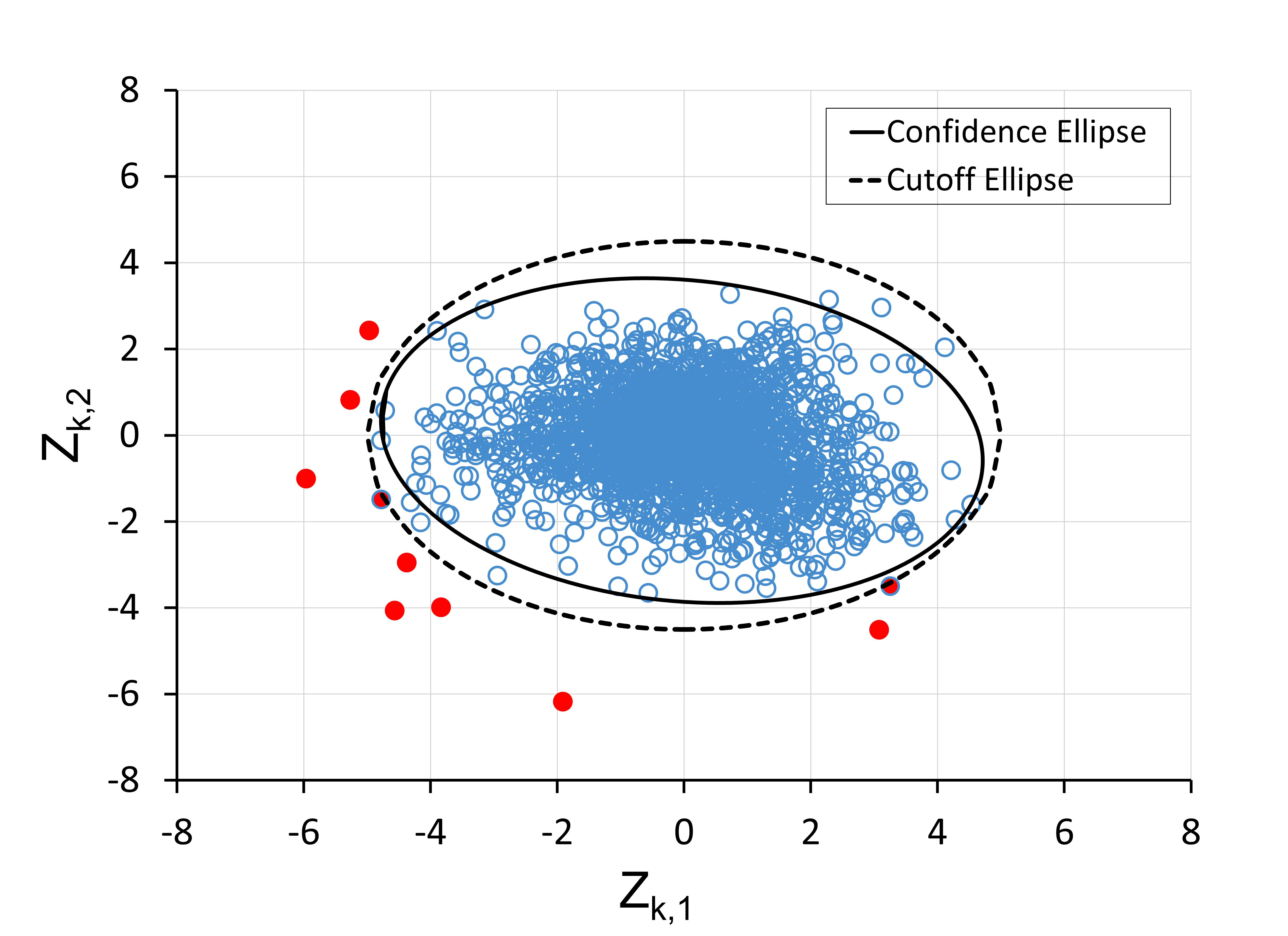
Fig. 7 Cutoff ellipse of axes 5.0 to 4.5 compared to a 99.9 percent confidence ellipse calculated for an LNA’s PC scores. The red circles outside the cutoff ellipse represent units that would be identified as outliers in Equation (4) and removed.
Results
The application of the ellipsoid decision method is compared to the previously used single-score cutoff method. In all cases, the Z scores are obtained in real-time using the process described in Figure 2. The two different outlier criteria are applied to the Z scores and their effectiveness compared. As in Figure 6, the graphs present each measure parameter separately as a function of the unit number, k, throughout the testing of a lot. Passing units are signified by a hollow blue circle, where outliers are shown in red.
Example 1 – Driver Amplifier
Figure 8 shows the results of applying the single-score cutoff method to a lot of driver amplifiers, DRIVER1, with n = 3 measured parameters: supply current (IDD), gain and output power are all shown separately. Note that there is an extreme outlier with an IDD of 116 mA (k = 3424), as well as some weaker outliers with low gain (k = 3889) and high output power (k = 4607), that were not identified by single-score cutoff.
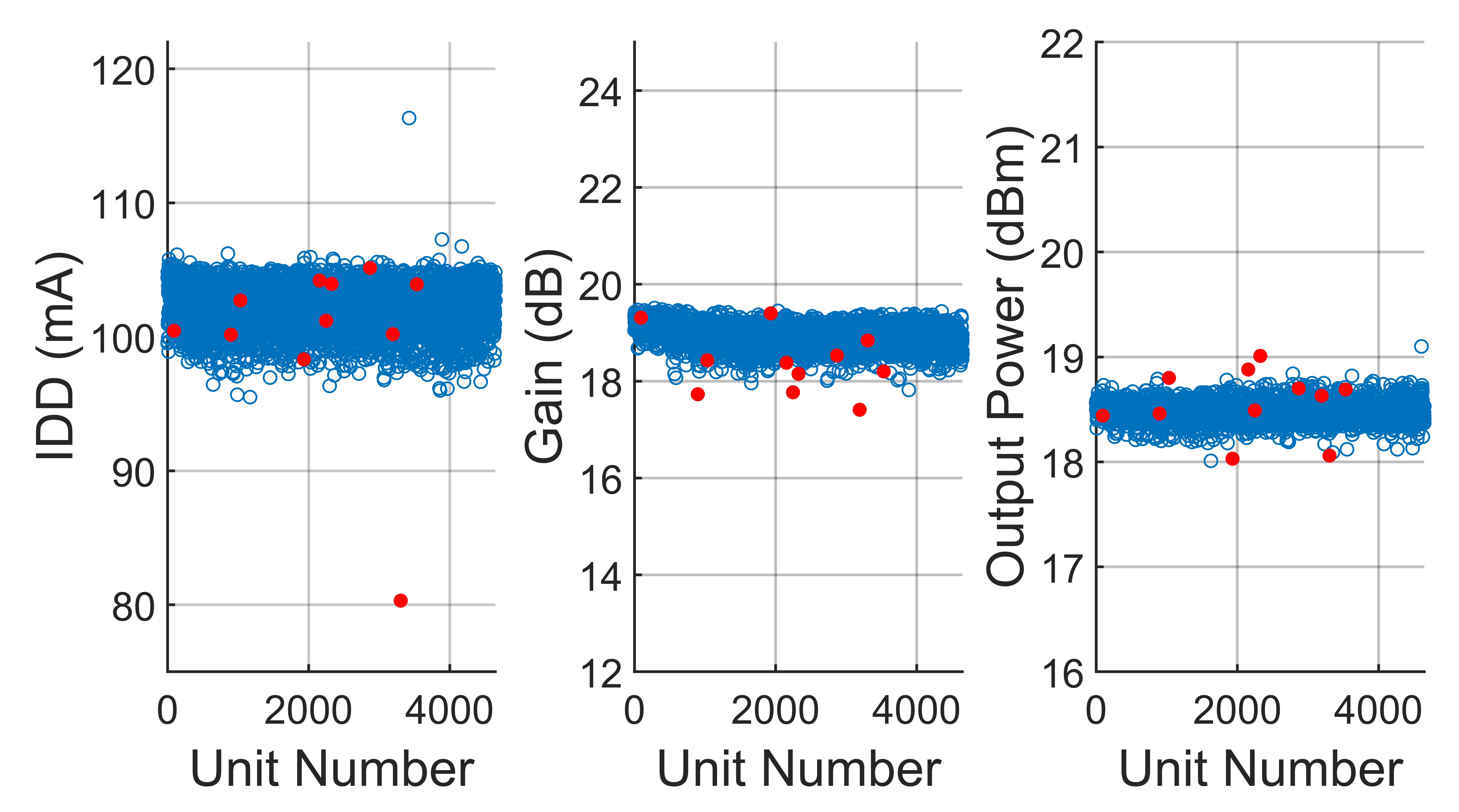
Fig. 8 Results from applying the single-score cutoff method to a lot of DRIVER 1 amplifiers. Passing units are in blue and outliers removed by the single-score method are in red. The cutoff threshold is 4.0.
An improved result is obtained when DRIVER1 is processed with the new ellipsoid method, as shown in Figure 9. The results are shown using axes lengths of 5.0, 4.5, and 4.0. Note that the previously missed outliers in IDD and output power are now identified. While the percentage of outliers removed by the ellipse cutoff method rises from 0.21 to 0.42 percent, the quality of removal is much better when compared to the single-score cutoff method.
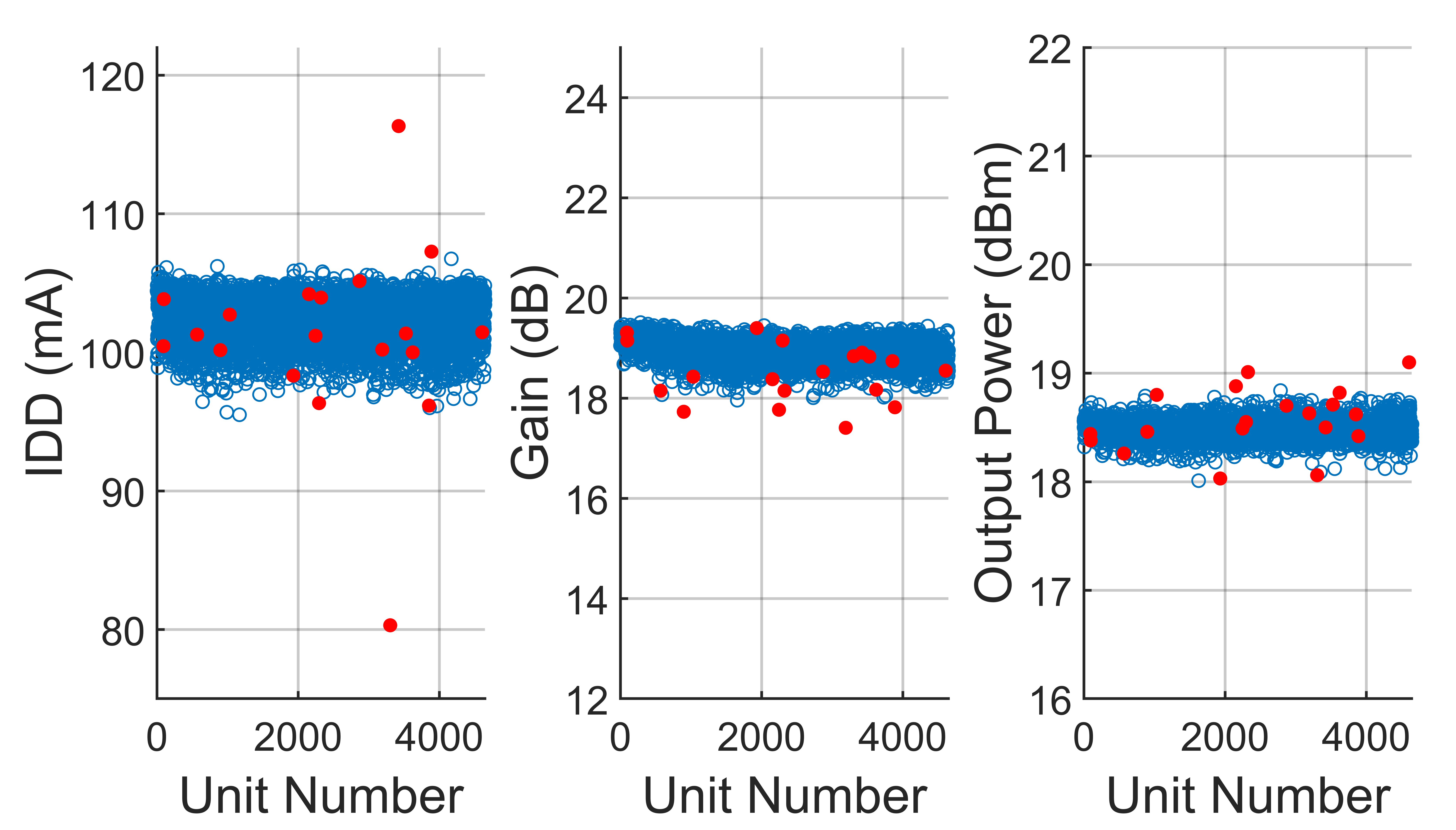
Fig. 9 Results from applying the ellipsoid method to a lot of DRIVER 1 amplifiers. Passing units are in blue and outliers removed by the ellipsoid method are in red. Cutoff axis lengths are 5.0, 4.5 and 4.0.
Example 2 – LNA
Figure 10 shows the results of applying the single-score cutoff method to a lot of low noise amplifiers, LNA1. Here there are n = 3 parameters: supply current (IDD), gain and noise figure. For LNAs, a wide variation in IDD can be quite common; however, as seen in Figure 10, the single-score cutoff processes this variation as abnormal and falsely identifies too many units as outliers.
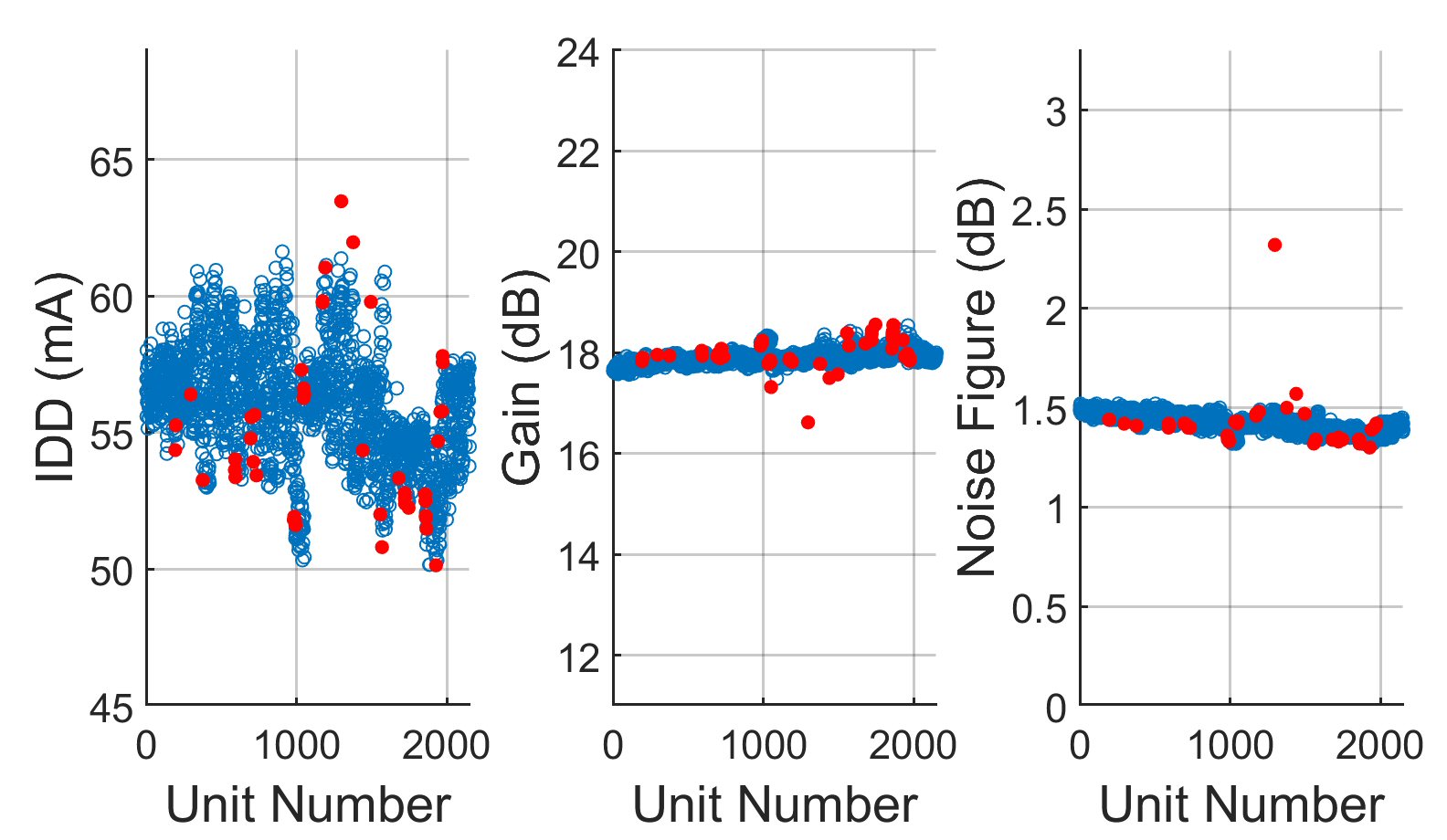
Fig. 10 Results from applying the single-score cutoff method to a lot of LNA1. Passing units are in blue and outliers removed by the single-score method are in red. The cutoff threshold is 4.0.
Figure 11 shows the results for LNA1 using the ellipsoid method with axes lengths of 5.0, 4.5, and 4.0. Note that the gross outliers are identified, but the number of total outliers has decreased 62 percent, from 45 to 18, with the reduction coming from false outliers which are now retained.
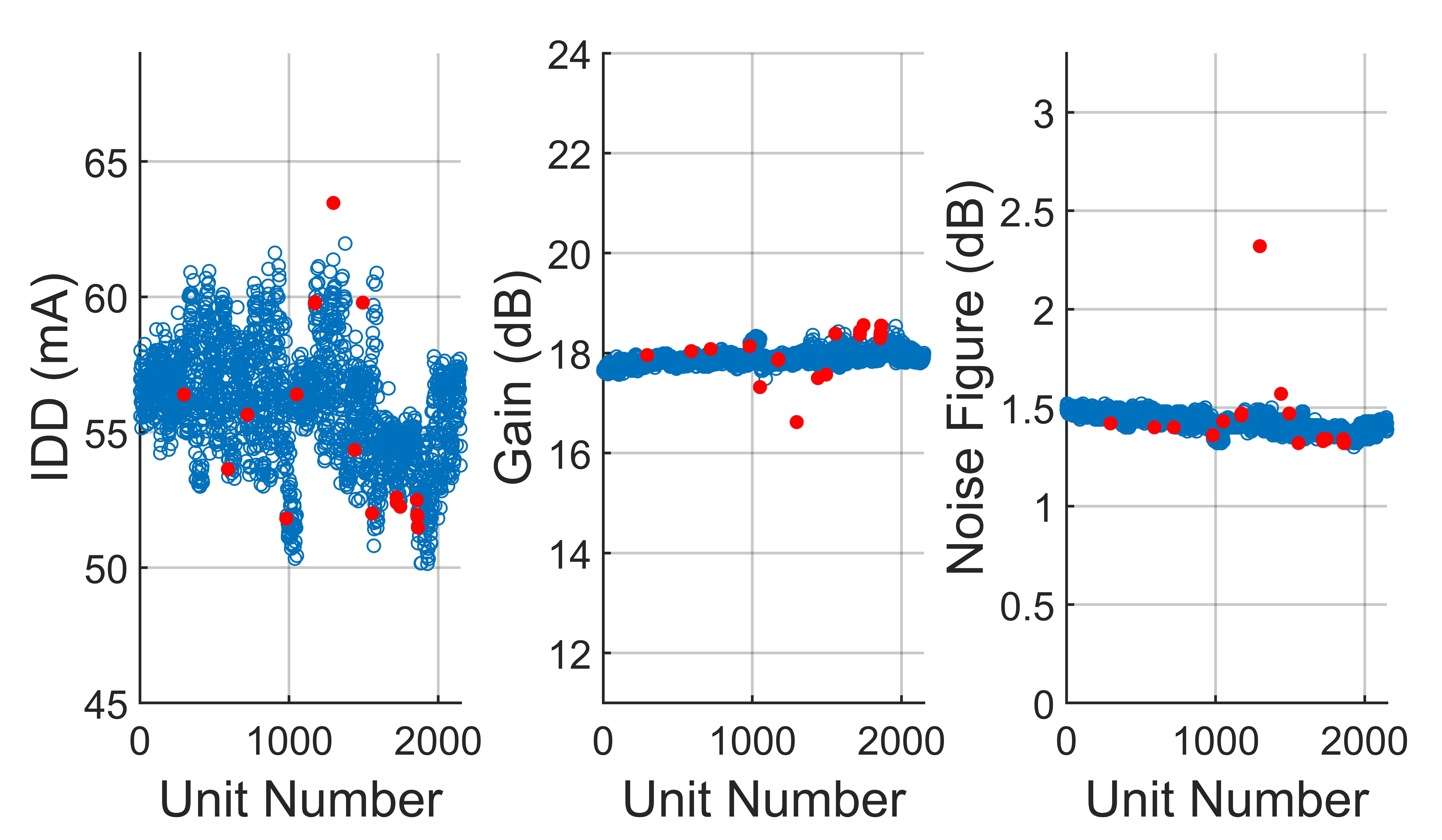
Fig. 11 Results from applying the ellipsoid method to a lot of LNA1. Passing units are in blue and outliers removed by the ellipsoid method are in red. Cutoff axis lengths are 5.0, 4.5 and 4.0.
Example 3 – DPST Switch
The next example shows where mechanical drift presents a challenge for outlier removal. The component in question is a double-pole single-throw (DPST) switch, SWITCH1, with n = 4 measured parameters: two insertion losses (ILA and ILB) and two isolations (ISO A and ISO B). In this figure, note that after the 2000th unit, ILA and ILB measurements begin to drift upwards, most likely due to a degradation in the contact set of the plunge test fixture; over time the material loses its elasticity and causes additional loss at high RF frequencies (this test was conducted at 10 GHz).
Figure 12 shows the results of the single-score cutoff method, which misses several outliers with high insertion loss, especially when the average begins drifting upward (above k = 2500). As shown in Figure 13, however, by applying the ellipsoid method with axes 6.5, 6.0, 5.5 and 5.0, those missed outliers are captured. The failed percent increases from 1.41 to 1.71 percent with 3341 units tested.
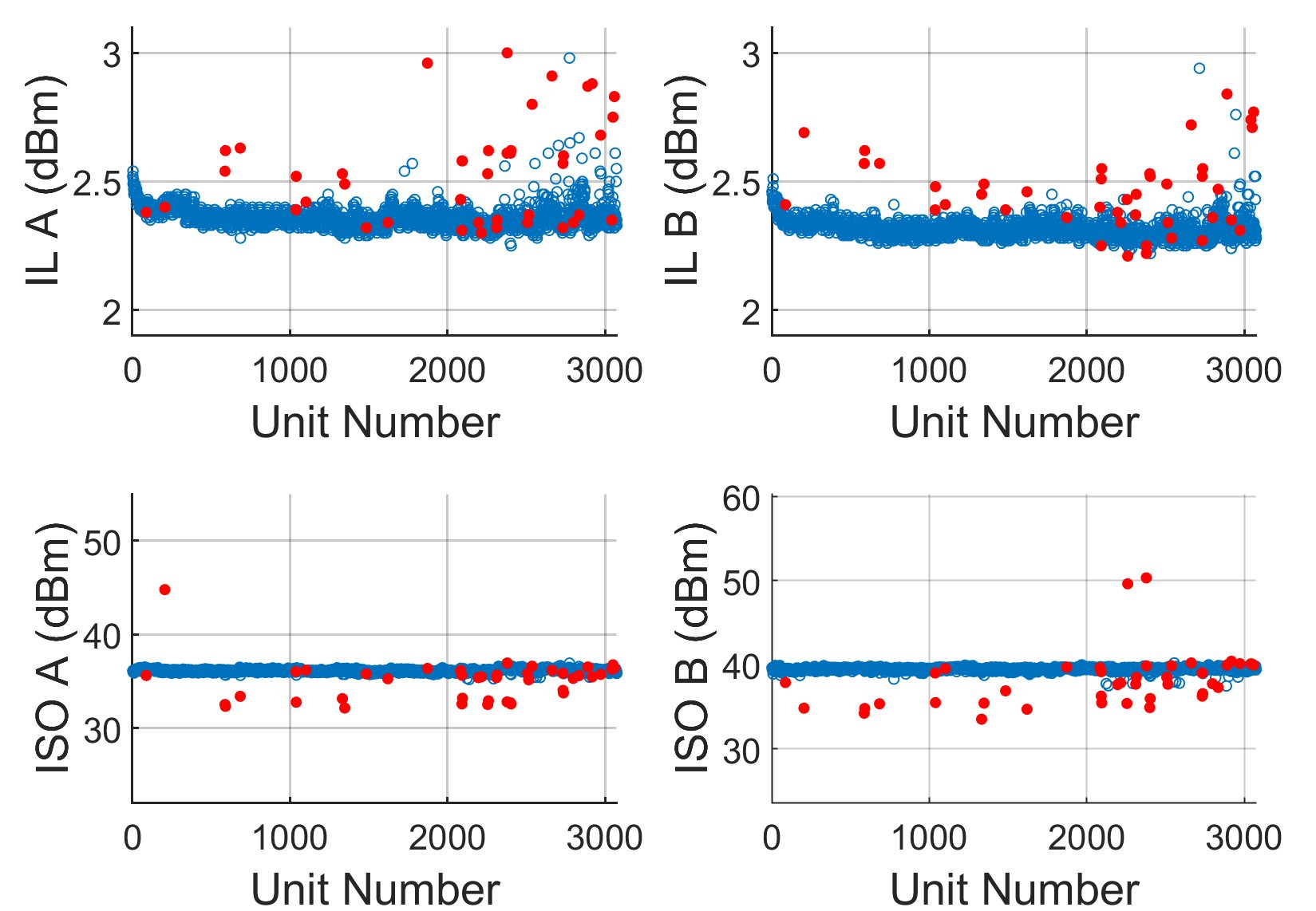
Fig. 12 Results from applying the single-score cutoff method to a lot of SWITCH1 DPST switches. Passing units are in blue and outliers removed by the single-score method are in red. The cutoff threshold is 5.0.
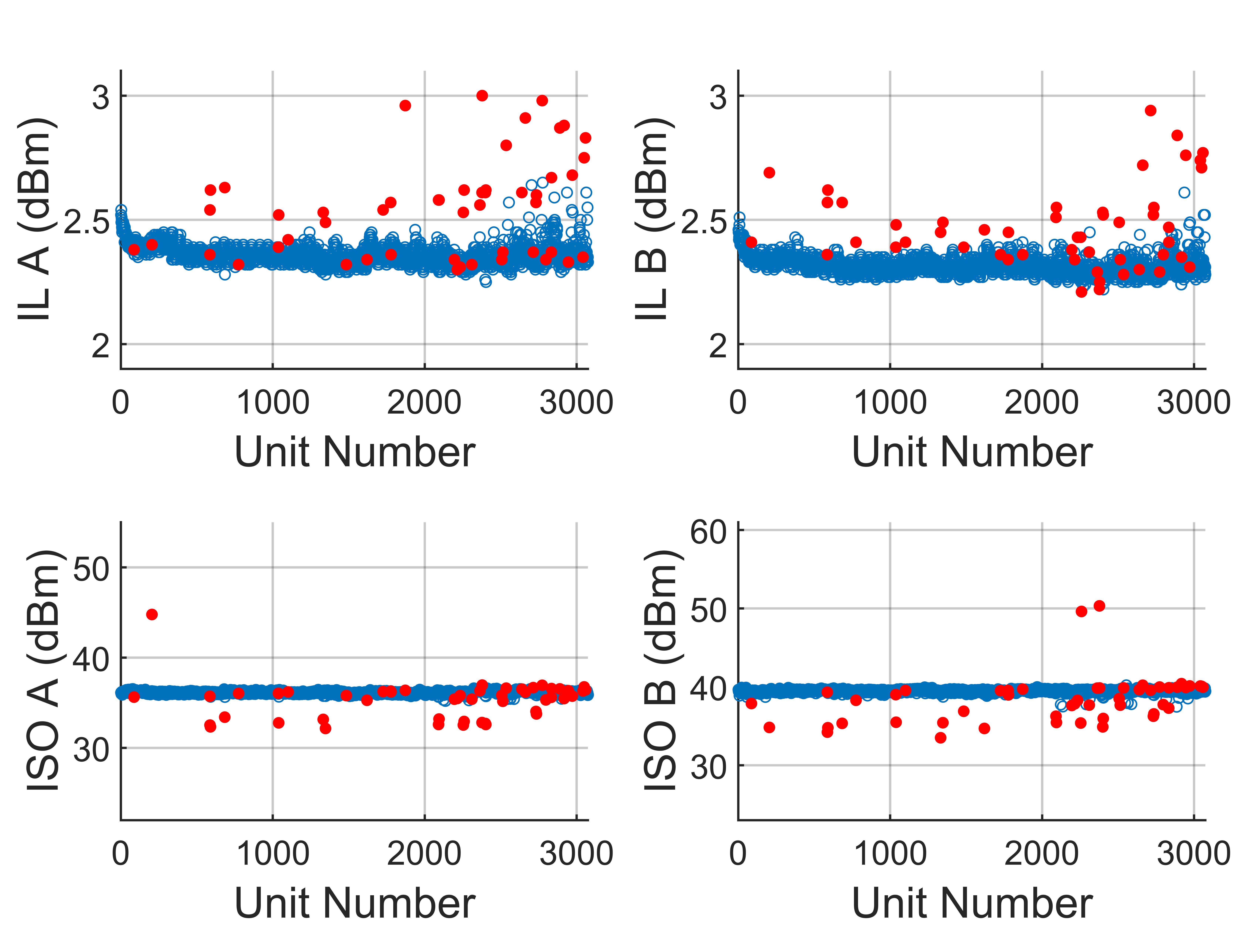
Fig. 13 Results from applying the ellipsoid method to a lot of SWITCH1 DPST switches. Passing units are in blue and outliers removed by the ellipsoid method are in red. Cutoff axis lengths are 6.5, 6.0, 5.5 and 5.0.
Example 4 – Mixer
Lastly, two methods for a lot of mixers, MIXER1 are compared. Here, there are n = 3 measured parameters: conversion gain, local oscillator (LO) isolation and IF/RF isolation. Figure 14 shows the results from applying the single-score cutoff method with a threshold of 5.0. Note two outliers in LO isolation that are not identified by this method (k = 2538, 2875). Figure 15, shows the results from applying the ellipsoid method with axes lengths of 6.0, 5.5, and 5.0. Note that the ellipsoid method identifies the missed outliers in LO isolation and still results in a lower failed percentage, with 31 percent less units failed.
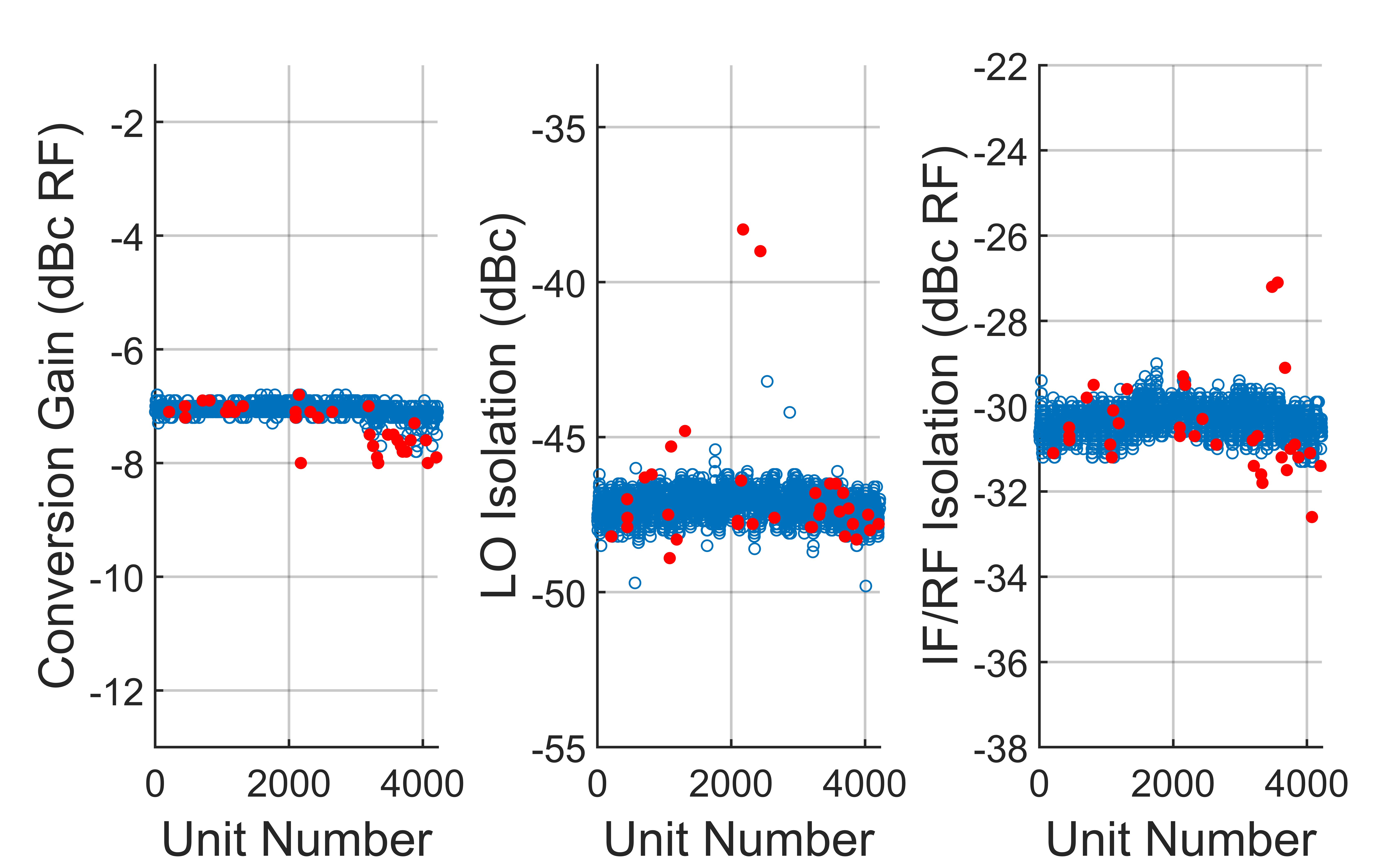
Fig. 14 Results from applying the single-score cutoff method to a lot of MIXER1 mixers. Passing units are in blue and outliers removed by the single-score method are in red. The cutoff threshold is 5.0.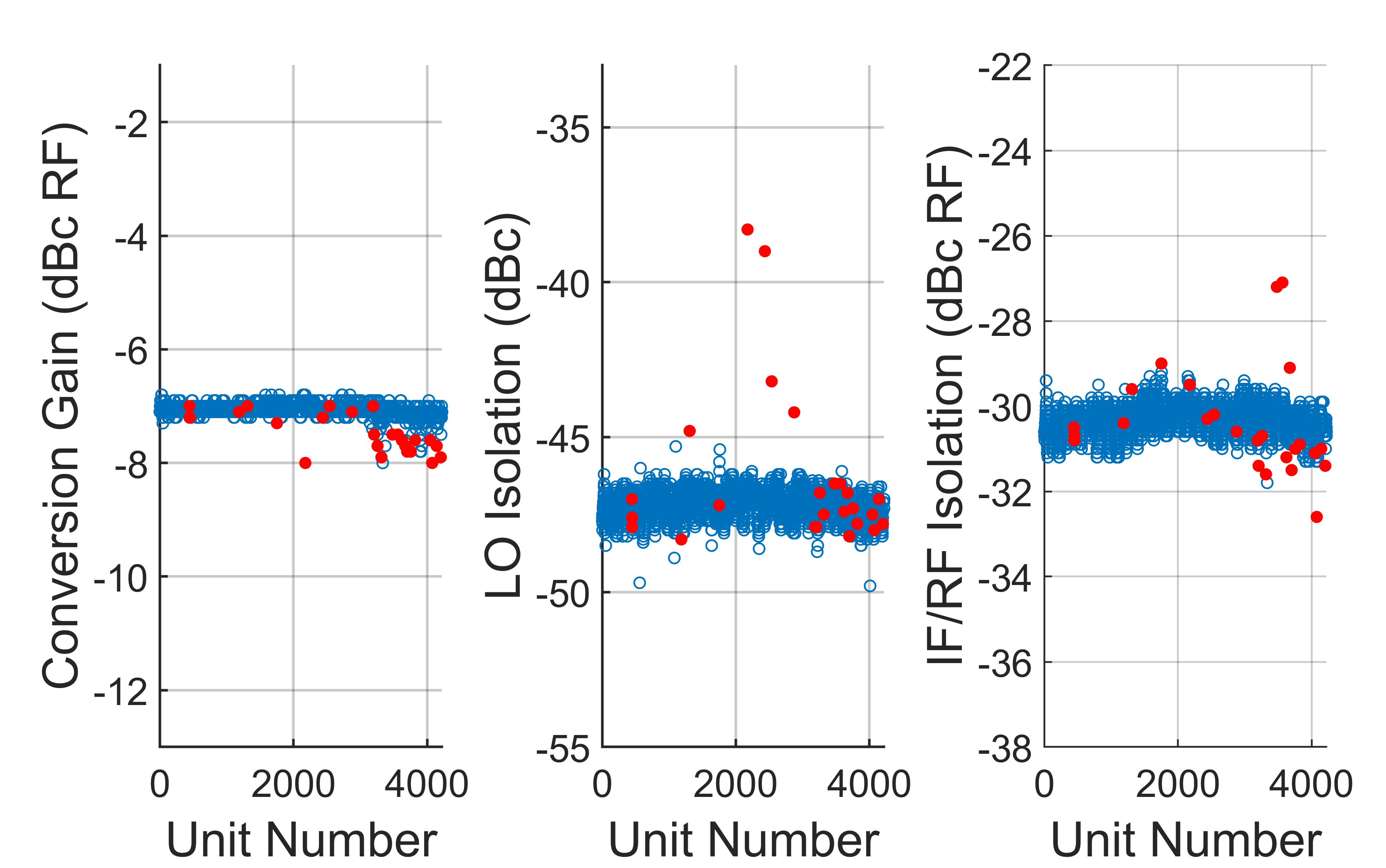
Fig. 15 Results from applying the ellipsoid method to a lot of MIXER1 mixers. Passing units are in blue and outliers removed by the ellipsoid method are in red. Cutoff axis lengths are 6.0, 5.5 and 5.0.
In addition to the units discussed in this section, the single-score cutoff method was compared to the ellipsoid method for over 50 lots of different LNAs, driver amps, switches and mixers, each consisting of 1000 to 10,000 devices. The results in all cases were like the examples presented here.
Conclusions
A real-time, adaptive algorithm for outlier removal using PCA and a new n-dimensional ellipsoidal criterion is described. This method is deployed on 50 lots of driver amplifiers, LNAs, mixers and switches and, in all cases, the ellipsoid method identifies gross outliers missed by the existing single-score decision method. Additionally, the ellipsoid method removes fewer false outliers (25 percent on average) thereby improving the overall yield.
Acknowledgment
The authors wish to acknowledge Helen Leung of Qorvo, Inc., who operated the automated test equipment.
References
- P. M. O'Neill, “Production Multivariate Outlier Detection Using Principal Components,” Proceedings of the IEEE International Test Conference, October 2008.
- A. Sharma, A. P. Jayasumana and Y. K. Malaiya, “X-IDDQ: A Novel Defect Detection Technique Using IDDQ Data,” Proceedings of the IEEE VLSI Test Symposium, April-May 2006.
- A. Nahar, R. Daasch and S. Subramaniam, “Burn-In Reduction Using Principal Component Analysis,” Proceedings of the IEEE International Test Conference, November 2005.
- A. S. Banthia, A. P. Jayasumana and Y. K. Malaiya, “Data Size Reduction for Clustering-Based Binning of ICs Using Principal Component Analysis (PCA),” Proceedings of the IEEE International Workshop on Current and Defect Based Testing, May 2005.
- A. Jauhri, B. McDanel and C. Connor, “Outlier Detection for Large Scale Manufacturing Processes,” Proceedings of the IEEE International Conference on Big Data, October-November 2015.
- H. Stratigopoulos, “Machine Learning Applications in IC Testing,” IEEE 23rd European Test Symposium (ETS), May-June 2018.
- E. Yilmaz, S. Ozev and K. M. Butler, “Adaptive Multidimensional Outlier Analysis for Analog and Mixed Signal Circuits,” Proceedings of the IEEE International Test Conference, September 2011.
- I. T. Jolliffe, Principal Component Analysis, Second ed., 2002.
- G. Remillard, C. Trantanella and M. Megan, “Removing MMIC Outliers in Production Test Using Real-Time Principal Component Analysis,” Microwave Journal, Vol. 62, No. 11, November 2019, pp. 68-80.
- L. Abu-Absi, C. Trantanella, A. Gopalan and M. Megan, “Advances in Real Time Adaptive Outlier Removal During MMIC Production Testing,” Microwave Product Digest, Vol. 32, No. 1, January 2021.
- A. Di Bella, L. Fortuna, S. Graziani, G. Napoli and M. G. Xibilia, “A Comparative Analysis of the Influence of Methods for Outlier Detection on the Performance of Data Driven Models,” Proceedings of the IEEE Instrument and Measurement Technology Conference, May 2007.
Biographies
A. Eisenklam is an undergraduate student in the School of Engineering at Vanderbilt University in Nashville, Tenn., partially supported by the Custom MMIC Women in Engineering scholarship. She is currently an engineering intern at Qorvo, Inc. in Chelmsford, Mass., working on algorithms for adaptive outlier removal in testing processes.
C. Trantanella received his B.S.E.E. degree in electrical engineering from Tufts University, Medford, Mass. in 1989, and his M.S. and Ph.D. degrees in electrical engineering from the University of Arizona, Tucson, Ariz. in 1991 and 1994, respectively. He is currently a Principal Engineer with Qorvo, Inc., in Chelmsford, Mass., engaged in the design of high frequency integrated circuits. Previously, he was a Principal Engineer at Hittite Microwave and Chief Scientist at Custom MMIC Design Devices, Inc.
