HARMONIC TUNING OF POWER TRANSISTORS BY ACTIVE LOAD-PULL MEASUREMENT

TECHNICAL FEATURE

HARMONIC TUNING OF POWER TRANSISTORS BY ACTIVE LOAD-PULL MEASUREMENT

Abstract:

A nonlinear network analyzer combined with an active multiharmonic load-pull system is described. Data acquisition uses an HP 71500 microwave transition analyzer (MTA) and force/sense bias supplies. Complete tuning and monitoring of the incoming and outgoing signals up to the third harmonic provide frequency and time domain characterization of the nonlinear transistor behavior. Signal compression curves, load-pull contours with harmonic tuning, DC and RF IV curves, and dynamic load lines are included. Typical measurements at 2 GHz show the influence of harmonic tuning on the operation of a 1 W power GaAs heterojunction bipolar transistor (HBT).

P. HEYMANN, R. DOERNER AND M. RUDOLPH

Ferdinand-Braun-Institut für Höchstfrequenztechnik

Berlin, Germany

 

Maximum power transfer between source and load requires conjugate matching. However, if the source is a nonlinearly driven transistor, the load reflection coefficient Gl that meets this condition depends on the power level. The systematic collection of output power Pout, power-added efficiency (PAE), gain G and bias as a function of Gl is called load-pull measurement. All microwave device manufacturers engaged in power transistor and power amplifier (PA) development routinely make this measurement, which provides the basic information needed for developing new transistors and makes available the modeling data required in nonlinear circuit design.1

An active, multiharmonic load-pull measurement setup is described that produces the well-known contours in the Gl plane, marking specified Pout or PAE. The measurement of RF current and voltage in the transistor at a strong nonlinear drive level allows optimization of the transistor operation. The measurements are made at maximum Pout, PAE, best linearity and suitable Gout, avoiding high voltage breakthrough and other current-voltage waveform shaping effects. One important question is "How do the load impedances at the higher order harmonics influence these quantities?" Time domain measurements are very useful for this purpose.2 Measurements are presented at a fundamental frequency of 2 GHz and its second- and third-order harmonics on a GaAs power HBT at low 3 V bias voltage because this is of special interest for mobile communication applications.3

 

ACTIVE OR PASSIVE LOAD PULL?

Active load pull is widely accepted as a method for characterizing power transistors in the microwave frequency range.4 The main advantage over passive methods is the theoretically unlimited range of Gl (including |Gl| = 1), which enables conjugate complex loading at the fundamental frequency and proper termination at the higher harmonics. Passive load pull can be used if the losses between the tuner and the device under test (DUT) and inside the tuner itself are sufficiently small. However, power transistors often require Gl near unity for output match. For example, HBT power cells for handsets in mobile communication need operation at Vce £ 3 V but show output resistances of less than 5 W, which must be matched at more than 1 W output power. Strong transformation with a passive tuner always yields high losses that can be corrected by calibration of today's high precision tuner systems. However, the need for at least a probe and a cable between the DUT and the tuner prevents access to the |Gl| range right next to the short.

At 2 GHz, a mechanical tuner including cable, bias-tee and microwave probe has 6 dB loss when transforming from 50 to 5 W. When the reflectometers between tuner and DUT are necessary for the vectorial RF current-voltage measurements, the loss is even higher. The ability to reach |Gl| = 1 (short, open) at the harmonics is important for the described system with harmonic tuning and can be realized only by an active system. While active load pull is the method of choice, it is not without serious limitations. The main problem is to provide the power for the reflected signal a2 from the active load to the highly mismatched transistor output, as shown in Figure 1.

The maximum power delivered to the load in the case of conjugate match (Gl = Gout*) is given by

where the signal ratio is determined by the reflection coefficient

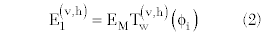
This relationship yields the power a22 from the active load, which generates the required reflection coefficient at a specific level of output power, as shown in Figure 2:

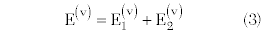
This power strongly increases with decreasing output resistance of the transistor. Thus, handling problems, particularly in on-wafer measurement systems, are to be expected. For example, the realization of Gl = 0.92/180° (Zout = 2 W real) for a 2 W transistor requires 12 W from the amplifier feeding the reflected signal a2. In addition, the unavoidable loss in cables, directional couplers, bias-tee, switches and probes makes the short inaccessible. While this fact is well known in passive load-pull setups, it also exists in active load systems, although at a different impedance level.

Fig. 2 Power of the reflected signal a2 required for load match vs. transistor output resistance for various output power levels.

Fig. 3 The 2 GHz active harmonic load-pull system.

 

MEASUREMENT SYSTEM

Figure 3 shows a block diagram of the measurement setup comprising an on-wafer nonlinear network analyzer and active harmonic load-pull system for frequencies between 0.5 and 18 GHz. (The actual frequency range depends on narrowband components such as PAs and circulators.) The fundamental output (2 GHz) of the synthesizer is split into a source and three load parts. The fundamental wave a1 is fed to port 1 via PA 1 (2 W), a bias-tee and reflectometer RI. The wave incident to port 2 is adjusted in magnitude and phase with respect to a1 by an attenuator (79 dB, 1 dB step) and variable phase shifter. It is amplified by PA 2 (8 W) and forms the fundamental signal a2. The output bias-tee must meet the requirements of testing high gain, broadband power devices in addition to withstanding more than 10 W RF power and 2 A DC current and providing very low reflection down to a few megahertz in order to prevent oscillations of the DUT.

The second- (4 GHz) and third- harmonic (6 GHz) signals are generated by a frequency doubler and tripler, respectively. These waves are adjusted in magnitude and phase, amplified to 1 W and combined by two directional couplers. The fundamental signal propagates in the main line to avoid any unnecessary loss. The other signals are coupled through the side arms. These three harmonics are superimposed at port 2 on the reflected signal a2. The transmitted signal b2 (including the harmonics) is absorbed by the circulator after passing the output reflectometer RII.

The signals at the input (a1, b1) and output (a2, b2) of the DUT are resolved by the reflectometers and measured by the HP 71500 MTA, an instrument similar to a vector network analyzer (VNA). The MTA measures complex wave ratios and scalar power values in the frequency domain and allows waveform measurements in the time domain at a very high dynamic range. The calibration of an MTA is the same as for a VNA (for example, short-open-line-thru), with the additional terms of power and phase distortion.5 (The ratio of the power in the main line of the reflectometer to the value indicated by the MTA sampler must be calibrated and used for correction.) For power tuning, three harmonics are included; for waveform measurements, up to six harmonics (12 GHz) are used. The reflectometers RI and RII must be calibrated for measurement of the complete wave situation using the MTA.

Fig. 4 Decrease in input reflection coefficient with increasing input power for various devices.

As shown previously, considerable power is required to realize the small optimum load resistance for a 3 V HBT. It should be mentioned that the power handling in the output part of the setup requires several precautions for DC and RF feed. Therefore, attenuators, phase shifters and most switches are located in the low power area of the system. At the highest power levels above 1 W, it is very important to avoid load states with high voltages instead of high currents inside the transistor. Practically, this condition means the device most likely will be destroyed when Gl is located off the real axis. Hence, an automatic search algorithm that moves around the optimum point unconstrained is not recommended. An interactive measurement procedure is the most appropriate. Harmonic signal stability problems do not appear since 2f and 3f are generated independently for the DUT by frequency multipliers. Nevertheless, harmonic tuning at the power limit of the device can be painstaking work. The mutual interdependence of fundamental power, active harmonic feed to port 2 and harmonic generation by the DUT itself requires prudent operation to measure Gl.

 

INPUT TUNER OR 50 W SOURCE?

While predistortion of the input signal can improve linearity or efficiency of a PA, it is not within the scope of this article. The sinusoidal source is of interest with respect to its available power and reflection coefficient. There are two solutions for the input feed: a 50 W source realized by a PA and an isolator, or insertion of a tuner for conjugate input match in order to boost the power gain. Both arrangements were tested in the described system. The test setup includes a mechanical input tuner. The HBTs dealt with are highly mismatched devices at both the input and the output. Typical values for |Gin| are shown in Figure 4. The change of S11 with increasing power is different for HBTs and FETs. Whereas the S11 of HBTs is nearly constant up to high power levels, FETs show a strong decrease due to the growing gate current.

Two other problems arise: A significant interdependence of Gin and Gl (particularly for bipolars) must be considered by changing the tuner transformation. In addition, the high input reflection coefficient Gin ª 0.95/180° of the HBT can hardly be matched by a passive tuner. Thus, even the strongest transformation cannot provide a conjugate source. This shortcoming is the same as discussed previously for the output match in passive load-pull systems for on-wafer measurements. The losses prevent the required transformation. The improved power transfer to the device is at the expense of increased losses in the tuner itself.

Another problem is to determine the value of Gs for the actual transformation state. If premeasured values are used, it is difficult to account for the changing Gin with power and Gl. Thus, the actual setting must be measured. Either way, the reflectometer RI is required in front of the DUT. The Gs measurement cannot be made without the switch between reflectometer RI and the DUT. The switch enables a stimulus signal to be fed in the opposite direction in order to measure the Gs coefficient in the network analyzer mode when the PA is switched off. Further error due to the tuner is introduced by the strong re-reflection of incident and reflected waves in the input line where the waves a1 and b1 are measured with the reflectometer RI. These disadvantages reduce the effectiveness of the tuner between the source and the DUT and, thus, the tuner is not used in this investigation and the measurements are made with the 50 W source only. The absence of re-reflections from the source means that the absorbed power of the DUT can be obtained from the difference of the power waves.

 

HARMONIC TUNING

Fig. 5 IV characteristics of a 10 (3 ¥ 30) GaAs HBT with load lines for harmonic tuning.

The limitation in output power of a transistor can be understood from its DC current-voltage characteristics, as shown in Figure 5. Using the device in low voltage amplifier operation (£ 3 V), not much clearance exists to extend the voltage swing downward. The device knee voltage VK marks the lower boundary (v(t) ? VK) and is determined by the ohmic region of a FET or by the saturation region of a bipolar junction transistor or HBT. Technological efforts to lower this value by reducing the parasitic resistances of the device are necessary but of limited use for this purpose. On the other hand, the maximum voltage can cause breakthrough (v(t) £ VBR). Possibilities exist for improvement of the device by optimum design. The current swing is restricted by the maximum current Imax of the device. Therefore, it is important to increase this value by technological measures.

Improvement of the power performance by means of harmonic tuning can be achieved by shaping the voltage waveform in such a way that the fundamental frequency amplitude becomes maximal. Superposition of harmonic sine waves with tunable phase and amplitude provides insight into the performance of power transistors and the shape of current and voltage in the output circuit of the device.6 It is generally accepted that only three harmonics can be effectively controlled in a practical circuit, particularly in MMICs.7 The number of circuit elements, the required expensive chip area for spacious passive components and the increasing loss of transformation elements prevent tuning of harmonics higher than the third one.

 

Simple analytic expressions for the superposition of voltage and current waveforms include

The DC bias (V0, I0) and voltage and current amplitudes of the fundamental and second- and third-harmonic waves (V1, V2, V3) and (I1, I2, I3) depend on the current-voltage characteristic of the transistor used.

The harmonic tuning effects are demonstrated on a GaAs HBT that has been developed as a low voltage power cell for applications in the lower gigahertz frequency range.3 Table 1 lists the HBT's key features. The boundary conditions are such that the actual currents and voltages do not penetrate into the prohibited areas of the IV characteristic. Thus, it must be assured that

Therefore, the amplitudes and phases of the harmonics must be arranged in such a way that the bottom of the voltage wave, for example, becomes flat and fits smoothly into the low voltage part of the DC IV characteristic.

These considerations lead to the Fourier coefficients of RF current and voltage as a function of the device properties, as listed in Table 2. The load reflection coefficient at the harmonic frequencies determines the class of operation, while the load at the fundamental frequency is conjugately matched. The first case (2f short, 3f open) is an approximation of class F operation with its attempt to square the sinewaves. The second case (2f open, 3f short) raises the peak voltage with the effect of higher Pout and PAE and has recently been referred to as tuned B operation.7

The Fourier coefficients are derived from the key features of power HBTs for tuned B operation. The knee voltage VK = 0.9 V at high collector current is obtained from the IV characteristic. The collector bias voltage V0 = 3 V is predetermined by the requirements of low voltage operation. The maximum current is assumed to be Imax = 1 A since it corresponds to a current density of 1.1 ¥ 105 A/cm2 and is not a hard saturation. This value is within the range of 1…2 ¥ 105 A/cm2, which determines the typical limit of these devices. The breakdown voltage VBR > 12 V is not reached and, therefore, is not a limiting parameter.

The superposition of the harmonics is such that

From the condition of maximally flat curves it follows that 9

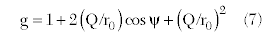
This relationship leads to

The results are shown in the previously displayed IV characteristics as well as the IC and VCE vs. time plots shown in Figure 6 and confirm that tuned B operation with a second-harmonic open and third-harmonic short is a promising concept for low voltage PAs when only these two harmonics are included. The time dependences of tuned B and class F harmonic control lead to the IV contours in accordance with Equation 4.

Fig. 6 The GaAs HBT device's (a) current and (b) voltage waveforms.

Fig. 7 Effects of harmonic tuning on Pout and PAE at the fundamental frequency.

Fig. 8 Pout and PAE at 2 GHz vs. the phase angle Gl at the 4 GHz second harmonic.

 

CURRENT-VOLTAGE HBT MEASUREMENTS AT 1 W POWER LEVEL

The distinctive feature of the presented system is its ability to measure RF performance at realistic power levels of 1 W and above and tune harmonic loads to any value on the Smith chart. The superposition of harmonic voltages and currents is a very simplified approach to the real situation in the output circuit of a PA. Nevertheless, it is clear that the waveforms become asymmetrical due to the harmonic content, and this asymmetry can be used to increase the amplitude of the fundamental wave (that is, the peak voltage can be greater than 2 ¥ (V0 – VK)).

Figure 7 shows typical Pout vs. Pin measurements for an HBT with an optimized load at 2 GHz. The saturated value is higher if the second harmonic is open instead of a short. Maximum Pout and PAE are shown in Figure 8 where the available source power is 22.5 dB and the load at 2 GHz (0.78 W/177°) is optimized for maximum Pout. When the phase of the load reflection coefficient at the second harmonic (4 GHz) is varied, a distinct minimum of both quantities is observed near the second-harmonic short (180°). This result is confirmed by harmonic balance calculations of the nonlinear transistor model.8

Fig. 10 Measured current-voltage contours using tuned B operation with three harmonics for an HBT with voltage peaking and optimum contour in the device's saturation range where Pout = 29.6 dBm and PAE = 51%.

The IV contours in the microwave range are strongly influenced by the reactive components of the transistor. Thus, the measured waveforms of a power HBT near the 1 dB compression point, as shown in Figures 9 and 10, indicate the wave shaping that actually can be achieved. The basic effect of harmonic tuning can be seen clearly. The reduction of Vl with a 2f short corresponds to squaring the sinewave (class F).9 The increase of Vl with a 2f open is the reason for increasing Pout and PAE (tuned B). In addition, the flattening of the bottom part, enabling the smooth fit to the left part of the IV characteristic, becomes obvious. These very peculiar waveforms can be verified only by a comprehensive nonlinear transistor model. On the other hand, verification of these measured waveforms and the other load-pull results from the model calculations represents the most stringent test of such a model.

The question of linearity arises because the high voltage amplitude at 2f is expected to deteriorate the intermodulation performance of the device. This possible disadvantage can be addressed by predistortion of the input signal. However, the realization of hybrid PAs reported by Heima et al.7 demonstrates that the adjacent-channel power rejection of tuned B is not worse than that of class F, while Pout and PAE are much better.

 

CONCLUSION

A powerful and affordable tool is described for nonlinear on-wafer measurements in the 0.5 to 18 GHz frequency range that is useful for designing high efficiency PAs for mobile communications. The device meets foundry requirements for tuning process parameters for new power transistors and tests nonlinear CAD models of those devices. One special feature is the access to vectorial RF current and voltage waveforms, which are the most important intrinsic parameters of transistor operation. These measurements can be performed at power levels of more than 1 W with |Gl| £ 0.9 for the fundamental wave and for |Gl| = 1 at the second and third harmonics.

References

1. M. van den Bossche, "Accurate and Traceable High Frequency Large Signal Measurements of Two Ports," Proceedings of HP Workshop, European Microwave Week, München, 1999, pp. 1/1–1/15.

2. J. Verspecht, P. Debie, A. Barel and L. Martens, "Accurate On-wafer Measurements of the Spectral Components of Incident and Scattered Voltage Waves at the Signal Ports of a Nonlinear Microwave Device," IEEE MTT-S International Microwave Symposium Digest, Orlando, 1995, pp. 1029–1032.

3. M. Achouche et al., "GaAs Power HBTs for Mobile Communications," GaAs 99 Digest, München, 1999, pp. 448–451.

4. P. Berini, M. Desgagne, F. Ghannouchi and G. Bosisio, "An Experimental Study of the Effects of Harmonic Loading on Microwave MESFET Oscillators and Amplifiers," IEEE Transactions on Microwave Theory and Techniques, Vol. 42, 1994, pp. 943–950.

5. G. Kompa and F. van Raay, "Error-corrected Large Signal Waveform Measurement System Combining Network Analyzer and Sampling Oscilloscope Capabilities," IEEE Transactions on Microwave Theory and Techniques, Vol. 38, 1990.

6. P. Colantonio, F. Giannini, G. Leuzzi and E. Limiti, "A Unified Approach to High Efficiency Microwave Power Amplifier Design," GaAs 99 Digest, München, 1999, pp. 272–275.

7. T. Heima, A. Inoue, A. Ohta, N. Tanino and K. Sato, "A New Practical Harmonics Tune for High Efficiency Power Amplifier," 29th European Microwave Conference Digest, München, 1999, pp. 271–274.

8. M. Rudolph, F. Lenk, R. Doerner and P. Heymann, "Influence of 2 GHz Harmonic Load-pull on HBT and MESFET Output Power and Efficiency," IEEE MTT-S International Microwave Symposium Digest, Anaheim, CA, 1999, pp. 741–744.

9. F.H. Raab, "Class F Power Amplifiers with Maximally Flat Waveforms," IEEE Transactions on Microwave Theory and Techniques, Vol. 45, Nov. 1997, pp. 2007–2011.

Peter Heymann received his Dipl. Phys. and Dr. rer. nat. degrees in physics from the University of Greifswald, Germany in 1963 and 1968, respectively. From 1963 to 1982, he worked on different projects in the field of wave plasma interaction, including wave propagation, RF plasma sources and heating, and microwave and far infrared plasma diagnostics. Since 1982, Heymann has been working on GaAs microwave electronics. In 1992, he joined the Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin. He currently is responsible for measurement, characterization and modeling of active and passive components of microwave MMICs.

Ralf Doerner received his Dipl. Ing. degree in communications engineering from the Technical University Ilmenau, Germany in 1990. Since 1989, he has been working on microwave measuring techniques. In 1992, Doerner joined the Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin. His current research is focused on calibration problems in on-wafer millimeter-wave measurements of active and passive devices and circuits and on nonlinear characterization of microwave power transistors.

Matthias Rudolph received his Dipl. Ing. degree in electrical engineering from Technical University Berlin, Germany in 1996. Since then, he has been working toward his Dr. Ing. degree at Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin. Rudolph's research focuses on characterization and modeling of FETs and HBTs.