In the fast moving, competitive world of nonlinear design, the ability to turn a new device technology into a final product in the minimum possible time is critical to a company’s success. A recent approach, which is gaining momentum, is the use of behavioral models. This combined with advances in the related test and measurement solutions is already showing dramatic reductions in product design cycles. This article looks at tailored measurement/modeling solutions from simple 50 ohm system level testing to full harmonic characterization with arbitrary impedance control required for Waveform Engineering.
Recent years have seen a surge in the interest in behavioral modeling of nonlinear devices, stemming from the release of a number of commercial, off-the-shelf solutions such as the Cardiff Model family. The expectations for such models are high; however, to get the most from them and to accurately simulate device performance, it is essential to fully understand how the model works along with the permitted application space.
Third-Order PHD Models
The Cardiff Model Lite (CML) is a third-order formulation that allows the extension of S-parameters under large signal operation. It is a poly-harmonic distortion (PHD) behavioral model formulation1 shown in Figure 1. It is based upon the harmonic superposition principle, which describes the large signal ‘B’ wave (Bpm) response, linearized around a large signal operating point (LSOP), in terms of a linear mapping with the other stimulus ‘A’ waves (Aqn).
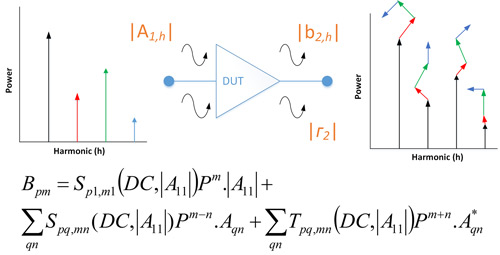
Figure 1 PHD model formulation.
The DUT is first driven with a fundamental tone, in this case A11. At each fundamental input power (A11), the device is simultaneously perturbated with a small signal tone at each harmonic frequency, Aqn – where q denotes the port index and n is the harmonic index. This is accomplished using the second source within a network analyzer.
The phase of this generator is swept with a minimum of six different phases, to allow the model to predict performance correctly. This perturbation process can be completed on both sides of the device, using the circuitry provided within the CML unit. Thus for each harmonic component, the corresponding model parameters, S and T, can be obtained by applying a least-squares fit algorithm to the measured data.
All third order behavioral models are local models; and as such, only valid for the applied operating conditions such as impedance, bias and temperature. If the measurement is performed correctly, the model will predict device performance to a high degree of accuracy within the measurement space, and will extrapolate gracefully.
Note that care must be taken with extrapolation, indeed such models can return completely ambiguous results if the user strays too far from the operating conditions of the measurement. A good way to think of this extrapolation process (in a non-mathematical way) is in the I-V space. The model extraction process for a PHD model uses a small-injected signal with rotating phase at the input and output of the device at the fundamental and harmonic frequencies.
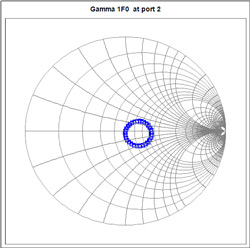
Figure 2 Typical impedance sweep using a F0 perturbation tone at the load-side.
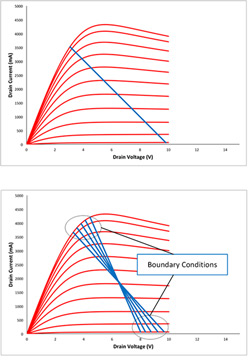
Figure 3 Load-lines at 50 ohm and as impedance is swept.
For simplicity, think about the fundamental frequency, the result of this injected signal is a variation in impedance. An example of this load variation or ‘load-pull’ performed for such a measurement is shown in Figure 2. Think about the I-V curves for a transistor as shown in Figure 3 and the RF load line you would expect when driven in to compression into the system impedance (nominally 50 ohm) as shown on the top of Figure 3. Now spin the load and, of course, the load line will move up and down effectively ‘mapping’ the device boundaries as shown on the bottom.
If we focus in on the knee region and impose a curve fit using the measured data, the measured data can be accurately modeled. A small extrapolation also does a good job; however, further extrapolation quickly leads to a breakdown of the model.
If used correctly, this model is an excellent way to get nonlinear data into a simulator, and should be thought of in a similar way to an S-parameter model – if a dense grid is used for frequency and bias, interpolation within the simulator will work well. Typical applications are in system level simulation where a number of 50 ohm components can be cascaded and analyzed in terms of fundamental and harmonic performance. A similar technique can also be used over load impedance, for example to model a power transistor for amplifier design; this is discussed in more detail later in this article.
Experimental Setup and measurement

Figure 4 Mesuro CML hardware.
The first stage here is to turn the VNA, capable of making only linear measurements, into a nonlinear VNA, capable of measuring the harmonic phase relationships. This can then be used to reconstruct time-domain waveforms. Here a phase reference is required to track the phase relationship as the frequency of the VNA is swept. The Mesuro/Rohde & Schwarz approach employs a conditioned, nonlinear device driven into compression at the fundamental frequency of the measurement. This offers improved harmonic content since the vast majority of the energy is focused at the measured frequencies, improving dynamic range for the initial characterization of the reference device as well as when the reference is used during nonlinear measurements.
For harmonic model extraction, additional hardware is required to route and combine signals to allow the required perturbation measurements at the input and output of the device. The CML unit (shown in Figure 4) integrates the phase reference with this signal conditioning hardware. The unit can be used with four-port R&S models, and solutions are available covering a range of frequencies up to 67 GHz.
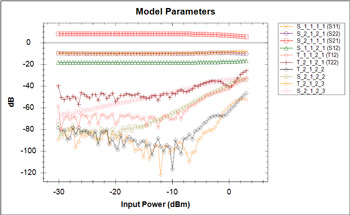
Figure 5 Extracted model parameters.
The CML generator software (see Figure 5) offers a suite which provides ease of setup and measurement flexibility to produce the best possible model. Features include:
- Device pre-characterization measurement allowing the user to understand the key parameters for the extraction.
- Flexibility in the number of phase points.
- Independent control of magnitude of the perturbation tones – with a source-power calibration for each harmonic.
- Post analysis tools showing the actual load perturbations conducted and the ability to verify the model fit against the measured dataset.
Load-pull, Waveform Engineering
Nonlinear devices cannot always be referenced to a 50 ohm impedance environment, and unlike linear S-parameters, it is not possible to transform data measured at one impedance to another. The measurement space required to capture the required design information, therefore, increases dramatically as the impedance space around the device must now be controlled.
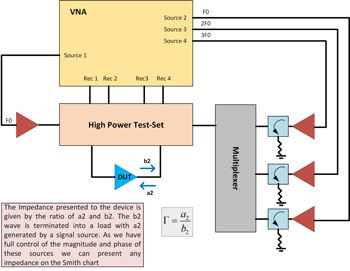
Figure 6 Schematic of open loop harmonic load-pull.
Importantly the same ‘building blocks‘ from the Cardiff Model Lite system can be re-used to realize a more capable system. Through the implementation of additional signal sources and a multiplexer, it is possible to create a system allowing the required impedance control at fundamental and harmonic frequencies. Then through variation of bias and impedance the waveform can be engineered to provide detailed insight into the DUT or optimize performance (Waveform Engineering). A schematic of an open loop active harmonic load-pull system is shown in Figure 6.
Open-loop active load-pull2 is an alternative to passive load-pull techniques,3 whereby the means of synthesizing the magnitude and phase of the reflected signal, ‘a2’ has been replaced by a phase-synchronized signal source(s). Note that for each controllable harmonic, an independent source is required.
Recent advances in VNA architectures fit perfectly with this approach. New four source VNA’s have direct digital synthesis (DDS) based sources, which is useful in a number of ways. Firstly, there are enough sources to drive the device while performing fundamental, second and third harmonic load-pull simultaneously. In addition, DDS sources do not drift in relative phase over time between multiple sources.
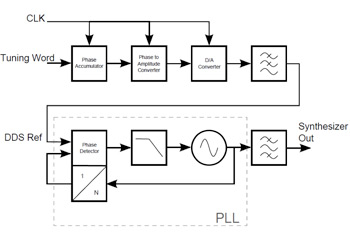
Figure 7 Schematic of a DDS based signal source.
In a DDS synthesizer, shown in schematic form in Figure 7, the tuning word defines the gradient of the phase change and by this the DDS frequency. The phase values are reconverted into digital amplitude values by the sine wave lookup table, e.g., from 0 to 65536 for 16 bit. A sine wave is created via a D/A converter; an anti-aliasing low pass filter is then used. This sine wave is used as a reference signal for a phase detector. The Phase Locked Loop (PLL) then locks the VCO's phase to the reference signal. This allows the setting of the VCO frequency by the DDS reference signal.
Such sources have many advantages over analog designs employing PLL, including improved phase noise, better frequency agility and precise control of the output phase and frequency. As the down-conversion local oscillator and all internal sources are driven from the same digital clock in this setup, there is no drift evident in the measured signals.
This was demonstrated in4 over a 24-hour period. There are two main benefits. Firstly, it allows for active load-pull at much higher frequencies where the drift between sources locked using analog PLL makes an active load-pull approach unpractical. In this solution, active load-pull at frequencies up to 60 GHz have been demonstrated. Secondly, as the LO is also locked to the signal generators, constant phase relationships from sweep to sweep are achieved resulting in time invariant waveform re-construction. This means that a phase reference is only required during calibration, thus allowing all sources in the VNA to be used during active harmonic load-pull.
Active Load-Pull and Waveform Engineering
There are numerous benefits to the active load-pull approach described here, including the ability to control impedance anywhere, inside and outside of the Smith chart; reduced system footprint and perhaps most importantly speed. A recent paper5 showed that using the same measurement instrument and setup; the speed of a 100-point load grid could be reduced by a factor of 7, from 4.5 minutes to only 41 seconds.
A patented quasi-closed loop architecture was also presented, showing where measurement speed is of the essence, such as in production environments. This architecture maintains the system stability of the open loop approach while offering further speed improvements; the same load-pull test is reduced to just 18.5 seconds.
The system can also be used to measure and engineer the terminal time-domain voltage and current waveforms. This approach can provide valuable insight to the designer. There are two main application spaces for Waveform Engineering.6 The first is on the process development side, where Waveform Engineering can be used to identify the root cause of process issues.7 The second application is optimization of device performance, allowing for the best possible design without the need for an iterative design approach.8,9
Case Study – Device Degradation
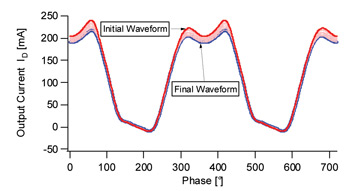
Figure 8 Output current waveforms showing degradation.
This case study7 looks at the use of Waveform Engineering to analyze a GaN HFET device that was suffering degradation in the field. Here a combination of RF and DC measurements were used to analyze the underlying cause of the problem. Figure 8 illustrates the degradation observed in the output current waveforms (100 waveforms overlaid) with the original waveform shown in red and the final waveform shown in blue.
There is a clear reduction in peak current, causing a drop in output power and efficiency. Next, a stress test was applied. To do this DC and RF measurements were conducted first at turn on and then after 90 minutes. DC I-V’s with overlaid RF load-lines (created by plotting the output voltage against output current) are shown in Figure 9; again red is the starting condition. The degradation can be seen both in the RF load-lines and the DC I-V’s after stress testing.
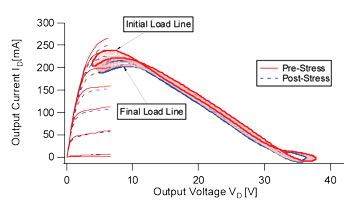
Figure 9 RF load-line and DCIV analysis pre and post stress.
Using Waveform Engineering it is possible to excite only part of the I-V space of the device. For example, by biasing the device at a low drain voltage with high quiescent current, then limiting the drive power, it is possible to excite only the high current region of the I-V space. Conversely, by biasing at a higher drain voltage and low quiescent current it is possible to excite only the high voltage region of the I-V space.
Although the RF remains unchanged pre/post stress in both cases if we look at the DC I-V’s it is clear that the device degradation is caused by high electric field in the high voltage region rather than thermal effect caused by high current. Armed with this additional information the process team could target their efforts and solve the issue in a timely manner.
Cardiff Model+
Having shown how useful the Waveform Engineering can be, this section looks at how to move the design process back to the simulator by means of a more advanced behavioral model. While behavioral modeling techniques such as X-Parametersä can be created to cover impedance, this requires the creation of a number of nonlinear models -- one for each impedance point. Interpolation is then conducted within the simulator.
In contrast, the Cardiff Model+ formulation, which is also a descendent of the PHD model formulation, extends the order of the formulation such that a single model can be used to fit an entire impedance space.10 This reduces the file size of the model.
Case Study – Cardiff Model+
This case study shows the process and results of modeling a 0.5 W PHEMT device at 9 GHz. In this case the model is for a fixed set of harmonic impedances, but these can also be included in the formulation if required. Once the load-pull has been completed the process of creating a model is simple: load the data into the model generator software, select the appropriate model type (in this case fundamental only) and export the model. The model can be exported in a format suitable for use in either ADS or Microwave Office®.
Once the process is completed it is possible to verify the results directly in the model generator. The exported model can be used within the CAD environment, see Figure 10, and can be used to look at traditional power and efficiency analysis as well as performing Waveform Engineering.
Figure 10 Model generator software.
Conclusion
This article has shown how advances in VNA technology can be combined with advances in nonlinear measurement solutions to ease the design process for new device technologies and modules integrating nonlinear devices. A simple behavioral model has been introduced and discussed along with its limitations as a local model. More advanced measurement systems building upon recent advances in VNA technology were also introduced showing how active load-pull can be used to improve the capability of load-pull benches.
Waveform Engineering was introduced with case studies in process development and high power amplifier design. A more advanced behavioral modeling formulation was also introduced, allowing a user to move the Waveform Engineering approach fully into a simulation environment.
References
- J. Verspecht and D. E. Root, “Poly-harmonic Distortion Modeling," IEEE Microwave Magazine 1527-3342/06, June 2006.
- Y. Takayama, “A New Load-Pull Characterization Method for Microwave Power Transistors,” MTT-S International Microwave Symposium Digest 1976, Volume 76, Issue 1, pp. 218–220.
- Technical Data Sheet 4T-070 Maury Microwave. “High-Gamma Automated Tuners (HGTTM).”
- A. Aldoumani, P.J. Tasker. R.S. Saini, J.W. Bell, T. Williams and J. Lees, “Operation and Calibration of a VNA-based Large Signal RF I-V Waveform Measurement System without using a Harmonic Phase Reference Standard,” 81st ARFTG Microwave Measurement Conference, June 7, 2013.
- T. Williams, B. Wee, R. Saini, S. Mathias and M. VandenBossche, “A Digital, PXI-Based Active Load-Pull Tuner to Maximise Throughput of a Load-Pull Test Bench,” 83rd ARFTG Microwave Measurement Conference, June 6, 2014.
- P. Tasker “Practical Waveform Engineering,” IEEE Microwave Magazine, December 2009.
- C. J. Roff. “Application of Waveform Engineering to GaN HFET Characterization and Class F Design,” PhD Thesis, University of Wales Cardiff, January 2009.
- M. Iwata et al., "First Pass Design of a High Power 145 W, High Efficiency Class J Amplifier using Waveform Engineering," IEEE Radio and Wireless Week 2013.
- P. Wright, J. Lees, J. Benedikt, P.J. Tasker, S.C. Cripps, "A Methodology for Realizing High Efficiency Class-J in a Linear and Broad-band PA," IEEE Transactions on Microwave Theory and Techniques, Vol. 57, No 12, December 2009.
- S.P. Woodington. R.S. Saini, D. Williams, J. Lees, J. Benedikt and P.J. Tasker, "Behavioral Model Analysis of Active Harmonic Load-pull Measurements," Microwave Symposium Digest, 2010.
