A compact, highly selective, bandstop filter (BSF) is presented with numerical and experimental results. It is additionally modelled with lumped circuit elements in an equivalent circuit model (ECM) to describe resonator coupling and corresponding phase shift. The filter is composed of two electrically small metamaterial cells in the form of fractal resonators. The physical size of the main filtering section is as small as λo/30 × λo/14.64, while the total size of the filter with the feed line sections is λo/10.53 × λo/6.6. Measurements demonstrate frequency selectivity of 63.80 and 92.10 dB/GHz at the lower and upper frequency band edges, respectively. The passband insertion loss is better than 0.5 dB below 0.6 GHz and above 2 GHz, with a minimum insertion loss of 0.1 dB. The signal suppression level is greater than 20 dB in the frequency band of 1.50 to 1.56 GHz.
Metamaterials are artificially structured materials composed of periodically arranged unit cells in a host medium in order to produce specific electromagnetic behaviours not observed in nature. The controllable engineering of electromagnetic material parameters in microwave component design enables new microwave applications.1-7 With the aim of miniaturization, alternative structures have been proposed,8-12 one of which is exploited in the design of this microwave BSF.
A magnetic metamaterial-inspired BSF is introduced to illustrate filter performance enhancement in a compact size. Microwave BSFs are widely used in transceivers to reduce distortion by suppressing spurious signals. They are attractive because they have better rejection than bandpass filters as the resonators in BSFs resonate not in the passband, but in the rejection band. In addition, the use of artificial metamaterials with self-resonating electrically small cells results in compact filters with high selectivity.13,14 Fractal resonators are used because they are self similar structures that fill any restricted area in a conformal manner while decreasing the resonant frequency.15 Thus, the spiralling form of fractal curves is the next miniaturization step for compact microwave component design.16
Fractal Resonator and BSF Design
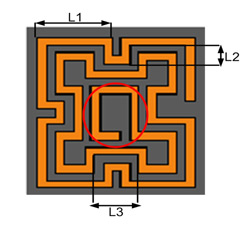
Figure 1 Fractal spiral resonator geometry.
The geometry of the fractal spiral resonator is shown in Figure 1. Each of the outer and inner fractal rings is the mirror image of the first order Hilbert fractal curve. These two concentric Hilbert fractal curves are then connected at one end to obtain a fractal spiral resonator. The circled section is an extension of the inner Hilbert curve, increasing its resonant length to compensate for the increased inductive and capacitive coupling between different sections. Substrate material is standard 0.5 mm thick Arlon DiClad 880 with dielectric constant 2.2. The metallization is copper. The copper line width and minimum distance between any two lines are 0.3 mm. The other geometrical parameters are L1 = 2.5 mm, L2 = 0.7 mm and L3 = 1.5 mm. The electromagnetic properties of fractal resonators are investigated extensively by Palandoken and Henke.16
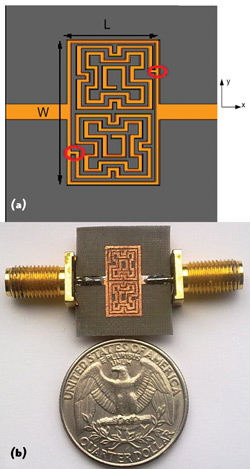
Figure 2 Numerical model results (a) and BSF fabricated prototype (b).
Results from the numerical model of the BSF along with the fabricated prototype are shown in Figure 2. Two fractal resonators are connected asymmetrically along the y-axis through the feed line in order to have symmetrical return loss. The resonators are separated from each other with a gap of 0.4 mm. Each is connected directly with the feed line to increase the field coupling (see the red circles in Figure 2a). To obtain low insertion loss in the passband, the two feed ports are connected through surrounding transmission line sections on the outer side of each resonator. The separation distance between the resonators and feed line sections is 0.3 mm. The filter width (W) and length (L) are 13.3 and 6.5 mm, respectively. The width of each metallic line is 0.3 mm except the width of the feed line, which is 1.5 mm to feed both resonators with 50 V line impedances at each port. The length of feed line sections at each port is 6 mm. The total size of the BSF is 18.5 mm.
The fractal resonators are fed directly through the feed line. The high impedance at the open end of each fractal resonator is then transformed into a low line impedance at the resonant frequency, as is the case for λ/4 resonators, in order to have high rejection in the stop band. In the passband, the incoming signal is transmitted with low insertion loss to the output port through the surrounding transmission line sections. The ECM of the BSF can therefore be derived as shown in Figure 3.
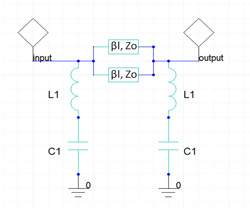
Figure 3 BSF equivalent circuit model with distributed and lumped circuit elements.
The fractal spiral resonator (res1) can be modeled as a series resonant circuit with corresponding inductor (L1) and capacitor (C1) due to the λ/4 resonance at the stopband frequency. The magnetic or electrical coupling between two fractal spiral resonators is negligibly small, as verified by numerical calculations with only one resonator and then with two resonators without any connecting transmission line sections. The surrounding transmission line sections are modeled as two parallel microstrip lines with electrical lengths of ßl and line impedance Z0. The input impedance of equivalent circuit is calculated as
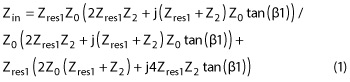
Where Z2 is the port impedance of second port, which is 50 Ω and

The input impedance is used to calculate the reflection and transmission parameters of the ECM. Ohmic losses are neglected for simplicity; however, these losses can be included in the formulation by substituting L and C with L* and C*, assuming that the R and Q values are known at a specific frequency.
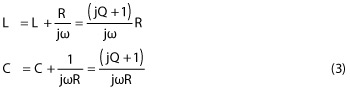
The S-parameters are easily calculated from the Z parameters of the symmetric equivalent RF circuit with only two unknown matrix elements, Z11=Z22 and Z21=Z12 for the lossy case. Z-parameters are calculated as
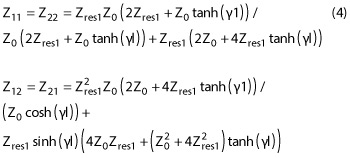
y =α + jb, where β and α are propagation and attenuation constants, respectively.
Return and insertion losses of the BSF are numerically calculated to determine element values of the ECM as a first order approximation. The fabricated prototype is also measured to illustrate the filter performance experimentally and validate the design principle.
Numerical and Experimental Results
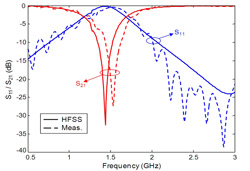
Figure 4 Measured and numerically simulated reflection/transmission parameters.
Numerical analysis of the BSF is done using Ansoft HFSS, which is an FEM-based 3D EM full-wave simulation program. The results are experimentally verified with measurements from a Rohde & Schwarz ZVB8 Vector Network Analyzer. As shown in Figure 4, the measured return loss is greater than 10 dB for frequencies lower than 0.8 GHz and higher than 2 GHz in the frequency band of 0.5 to 3 GHz, while the measured insertion loss is less than 0.5 dB in the passband. The measured rejection is greater than 20 dB in the frequency band of 1.5 to 1.56 GHz and 27.5 dB at 1.54 GHz. Numerical and experimental results agree well even though there are some ripples in the measured data as well as a small frequency shift between the numerical and experimental results due to fabrication, calibration and cabling-related errors.
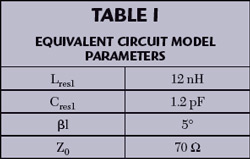

Figure 5 |S21| and |S11| of the ECM calculated by ADS.
The circuit element values of the ECM in Figure 3 are extracted by equations (1 through 4) and additional RF numerical simulations. They are tabulated in Table 1, neglecting ohmic losses as a first order approximation. RF performance of the ECM with tabulated element values is also verified by the circuit simulator in Ansoft Designer. S-parameters calculated by ADS are shown in Figure 5.
These results confirm the analytical formulation of the ECM. Figures 4 and 5 show that the ECM describes the frequency dependence of scattering parameters and the operation of the BSF quite well even though there are some discrepancies in the Q of the modelled and experimentally verified resonator designs. There are three main reasons for this. First, the capacitive and inductive coupling between fractal resonator and surrounding transmission line are neglected as a first order approximation. Second, the metallic loss, which degrades resonator Q, thereby affecting the resonant frequency and scattering parameters, is neglected for model simplicity. This is seen in higher return loss, lower insertion loss and higher Q calculated from the circuit model in comparison to calculations from the numerical model. Third, the circuit model is based on the calculation of circuit elements for a l/4 resonator. This is not true for frequencies far from resonance, however, where the wave feature of the RF signal must be modelled by distributed circuit elements or additional reactive lumped elements in a more complex circuit model.

Figure 6 BSF Resonant current distribution at the stopband frequency, magnitude (a) and direction (b).
The operating principle of the BSF can be described with the help of the ECM in Figure 3. Transmission of the incoming signal is blocked in the stopband by the λ/4 spiral resonator. The electrical lengths and field coupling emerging from the surrounding transmission line cause the identical fractal resonators to split into two resonances. The resonant field distribution is shown in Figure 6. As a result of the λ/4 resonance, the high impedance at the open end of each fractal resonator is transformed into a low impedance at the feed line with high reflection at the resonant frequency.
The frequency selectivity of the BSF is 63.8 and 92.1 dB/GHz at the lower and upper 3 dB frequency band edges. The measured resonant frequency is shifted from the calculated resonant frequency by 100 MHz. This is due mainly to fabrication-related geometrical differences and calibration imposed measurement deviations, which could be deduced from S11 and S21. This filter has no matching network, which is advantageous in reducing its physical size. The physical size of the main filtering section is λ°/30 × λ°/14.64 at 1.54 GHz, which is quite compact in comparison to the conventional stepped impedance or coupled line filters. The total size of the filter with the transmission line sections at input and output ports is λ°/10.53 × λ°/6.6.
Conclusion
A compact, high selectivity BSF composed of two metamaterial cells of spiral fractal resonator is modelled with lumped and distributed circuit elements in an ECM to explain the functional description of spiral resonators and surrounding transmission line. The total physical dimensions of the BSF are λ°/10.53 × λ°/6.6 with a very compact main filtering section of λ°/30 × lo/14.64. The insertion loss is better than 0.5 dB in the frequency band lower than 0.6 GHz and higher than 2 GHz with the minimum insertion loss of 0.1 dB. No matching network is required, which effectively reduces the total filter size. Insertion and return loss are numerically calculated and experimentally measured, showing good agreement with the ECM. Frequency selectivity of 63.8 and 92.10 dB/GHz at the lower and upper frequency band edges makes the filter quite suitable for use in modern communication and sensor applications.
References
- G.V. Eleftheriades and K.G. Balmain, Negative Refraction Metamaterials: Fundamental Principles and Applications, NJ, Wiley Interscience, 2005.
- T. Kodera, D.L. Sounas and C. Caloz, “Magnetless Nonreciprocal Metamaterial (MNM) Technology: Application to Microwave Components,” IEEE Transactions on Microwave Theory and Techniques, Vol. 61, No. 3, March 2013, pp. 1030-1042.
- Y. Dong and T. Itoh, “Promising Future of Metamaterials,” IEEE Microwave Magazine, Vol. 13, No. 2, March 2012, pp. 39-56.
- W. Zhang, H. Chen and H.O. Moser, “Subwavelength Imaging in a Cylindrical Hyperlens Based on S-String Resonators,” Applied Physics Letters, Vol. 98, No. 7, February 2011, pp. 073501-073501-3.
- S. Yun, F. Namin, D.H. Werner, T.S. Mayer, C. Bungay, C. Rivero-Baleine and L. Zhang, “Demonstration of a Nearly Ideal Wavelength-Selective Optical Mirror Using a Metamaterial-Enabled Dielectric Coating,” Applied Physics Letters, Vol. 102, No. 17, April 2013, pp. 171114–171114-5.
- Z. Zhu, X. Zhang, J. Gu, R. Singh, Z. Tian, J. Han and W. Zhang, “A Metamaterial-Based Terahertz Low-Pass Filter With Low Insertion Loss and Sharp Rejection,” IEEE Transactions on Terahertz Science and Technology, Vol. 3 , No. 6 , November 2013, pp. 832–837.
- C.H. Liu and N. Behdad, “Tunneling and Filtering Characteristics of Cascaded-Negative Metamaterial Layers Sandwiched by Double Positive Layers,” Journal of Applied Physics, Vol. 111, No. 1, January 2012, pp. 014906-014906-9.
- Z. Wu, Y. Shim and M. Rais-Zadeh, “Miniaturized UWB Filters Integrated With Tunable Notch Filters Using a Silicon-Based Integrated Passive Device Technology,” IEEE Transactions on Microwave Theory and Techniques, Vol. 60, No. 3, March 2012, pp. 518-527.
- K. Mo, Q. Wang, D. Song and Y. Tan, “A Novel Compact Ridge Waveguide Band-Stop Filter for Harmonic Suppression,” International Workshop on Microwave and Millimeter Wave Circuits and System Technology, April 2012, pp. 1–3.
- J. De Dios Ruiz and J. Hinojosa, “Shunt Series LC Circuit for Compact Coplanar Waveguide Notch Filter Design,” Microwaves, Antennas & Propagation, IET, Vol. 8, No. 2, January 2014, pp. 125-129.
- M. Hayati and A. Abdipour, “Compact Microstrip Lowpass Filter With Sharp Roll-Off and Ultra-Wide Stop-Band,” Electronics Letters, Vol. 49, No. 18, August 2013, pp. 1156-1160.
- R. Habibi, C. Ghobadi, J. Nourinia, M. Ojaroudi and N. Ojaroudi, “Very Compact Broad Band-Stop Filter Using Periodic L-Shaped Stubs Based on Self-Complementary Structure for X-band Application,” Electronics Letters, Vol. 48, No. 23, November 2012, pp. 1483-1484.
- R. Marques, F. Martin and M. Sorolla, Metamaterials with Negative Parameters: Theory, Design and Microwave Applications, NJ, Wiley-Interscience, 2007.
- C. Caloz and T. Itoh, Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications, NJ, Wiley-Interscience, 2007.
- N. Engheta and R.W. Ziolkowski, Electromagnetic Metamaterials: Physics and Engineering Explorations, NJ, Wiley-IEEE Press, 2006.
- M. Palandoken and H. Henke, “Fractal Spiral Resonator as Magnetic Metamaterial,” IEEE Applied Electromagnetics Conference, December 2009, pp. 1-4.
