
Figure 1 Parabolic reflector for a point to point microwave link, compared to small flat array for mm-wave.
Operators of backhaul networks are facing more and more problems when it comes to new installations. In congested areas, the site acquisition is a substantial part of the cost and house owners and planners are often hesitant to allow access to rooftops, etc. Also, for aesthetic reasons, antennas can be disguised to blend in with the environment and take shape as part of the chimney, brick walls and the like. Furthermore, from a practical point of view, a minimized wind load and weight is advantageous, especially during installation. Figure 1 offers a comparison between standard and mmWave antennas.
Size
Antenna size is always something that must be related to the wavelength and thus the frequency. Higher frequencies can utilize smaller antennas but antennas cannot be made arbitrarily small and still perform without detriment to performance. There are two main constraints when it comes to antennas and size. One is the radiation resistance and the antenna feeding impedance and the other is radiation pattern. The first issue, impedance and matching for electrical small antennas has been successfully addressed by antenna and circuit designers, with virtually all antennas used in handsets being small from an electrical point of view, yet they perform well for their application.

Figure 2 Spherical coordinates of the isotropic radiator and pencil beam antenna.
The other constraint, antenna radiation pattern, is not so easy to compensate for as the fundamental laws of physics apply. In order to direct the electromagnetic energy from an antenna, it must have a certain shape and size. To be able to gain some insight into this, let us take a look at the most fundamental antenna, the isotropic radiator. A point source that serves as the basic antenna element for theoretical analysis will radiate equally in all directions. A hypothetical point source in (free) space will thus radiate in all directions in a spherical fashion – an isotropic antenna.
Of course, even the remote presence of a ground surface or conductors to this antenna element will cause a disturbance in its radiation pattern, and it will no longer radiate equally in all directions. However, as an analysis tool the isotropic point source is very useful and most, if not all, antenna structures can be treated as a combination of isotropic radiators.
Directivity
When dealing with antennas, there are a number of parameters to consider. This article will focus on antennas that have an appreciable size compared to wavelength, and where matching and radiation efficiency is generally not a big concern. Most of the energy supplied to the antenna from the transmitter is transformed to radiated energy, in one direction or another.
If we consider the directive gain first, the term implies that we seek a measure of the antenna’s ability to concentrate its energy in a certain direction. This is compared to the isotropic radiator as shown in Figure 2.
The isotropic radiator sends all its energy equally distributed in all directions, but any other physical reliable antenna will concentrate its energy in specific directions. For a point to point link, the preferred pattern is to direct all the energy in a small cone towards the receiving antenna. Other radiation patterns can also be desirable, such as broadcast antennas radiating their energy in a doughnut shaped pattern with the antenna in the center. Another example is a radar antenna that has a narrow horizontal beam and a broad beam in azimuth.
For a given antenna with a spatial dependency of the power density, Poyntings vector Sr has only a radial component in the far field.Sr [W/m2] is a function of θ, Φ and r as shown in Figure 3.
Total radiated power from the source is:
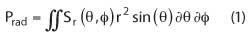
Figure 3 Definition of coordinates, Poyntings vector.
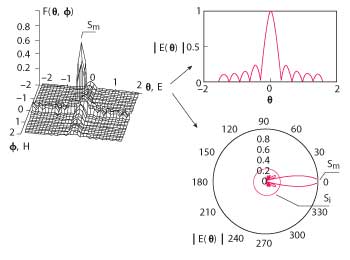
Figure 4 Antenna diagram as two dimensional contour plot showing E and H field components, and projection of the E-field pattern on θ plane in rectangular and polar plot. All scales are normalized to the maximum value of each parameter.
For the isotropic radiator, the power density Si is equally distributed over the area of the sphere, and thus

For the general case when there is a spatial dependence, Sr is given as a product of its maximum value Sm, and a function of the spherical coordinates F(θ, Φ).
The two dimensional function F(θ, Φ) is the antenna pattern and can be illustrated in several ways. Quite often the antenna pattern is presented as a projection in either θ or Φ plane and the E and H vector is aligned with either coordinate, see Figure 4. Note that for the isotropic radiator F(θ, Φ) =1, and the maximum value Sm = Si everywhere on the sphere as shown in the polar plot in Figure 4.
The directivity is defined as the ratio of the maximum value of Sr (=Sm) to the average value of the power density, or
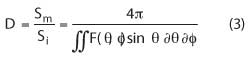
In words, the directive gain (D) is defined as the ratio of maximum power density to the average power density from the antenna. The average power density can be found by carrying out the integration of power at each infinitesimal area element on the imaginary sphere with radius R, or much easier, by calculating the equivalent power from an isotropic antenna,
Si=Prad/4πR2.
So far, the power Prad used in the equations is the power that is actually radiated by the antenna, to signify this the suffix rad is used. The input signal power to the antenna is generally different (higher). At this point, it may be convenient to discuss antenna gain, Ga. Any electrical structure is exposed to losses, even if very small there are some ohmic losses and also losses from reflection (mismatch) in most cases. If Prad is all the power actually emitted from the antenna in all directions, then the antenna efficiency can be written as η=Prad/Pin. Then the antenna gain is defined as Ga= ηD. In most cases, the antenna gain is almost the same as directive gain. From a system point of view the antenna gain is, of course, the interesting quantity since it goes directly into the link budget.
Another useful concept is the beamwidth. For the moment, the discussion is confined to pencil beam shaped patterns, the antenna pattern is basically symmetrical around the main axis of the beam as shown in Figure 2.
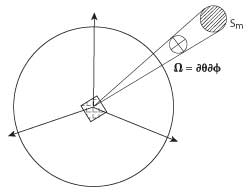
Figure 5 Equivalent cone shaped antenna diagram, useful for pencil antennas.
If the antenna radiation angle ΩA [sR] is defined as the imaginary solid angle through which all power would be concentrated if the power density was constant over that solid angle and equal to the maximum power density at boresight (the axis of the main lobe), we would find that: ΩA = 4π/D, and since ΩA ≡ φ1•θ1 for very small angles (see Figure 5), there is a simple and useful expression to approximately determine the beamwidth in either E or H plane,
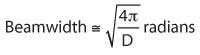
The approximation is good for small angles as found in highly directive antennas for point to point radios. For example, for a 36 dB antenna, the approximation will yield a beamwidth of
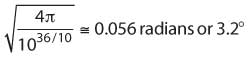
As an analogy, the antenna can be viewed as the spatial equivalent to the time-frequency concept for signals. The radiation pattern is the equivalent to the frequency plane and the physical distribution or separation of antenna elements is the time equivalence. Hence, like a short pulse gives rise to a broad frequency spectrum, a small antenna will have a broad spatial distribution of its energy (a broad beam). The underlying mathematics correspond and main lobe and side lobes can be calculated in a similar fashion.
RECEIVING SIGNALS
So far the discussion has revolved around the antenna as a radiator in the transmitting case. It would be a pity if we could not pick up the hopefully intelligent transmission in a complementary receiving antenna. To do this, two concepts are introduced: the effective antenna area and reciprocity.
The effective area of an antenna is defined as the power delivered on the antenna’s terminals divided by the power density that the receiving antenna is exposed to. In mathematical terms,

where Pr = Received signal power [W] on antenna terminals and Ae = effective antenna area [m2].
As mentioned earlier, we know that the power density from a transmitting antenna is
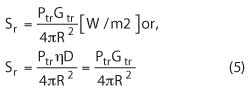
where Ptr = input power to transmitting antenna and Gtr = transmitting antenna gain.
The power delivered from the receiving antenna can now be calculated as:

It is obvious that the amount of received power is directly proportional to the effective area of the receiving antenna and this equation is valid regardless of frequency or wavelength.
We can now also appreciate the meaning of effective antenna area. As usual, whatever is introduced to measure or collects energy from a system will affect that system. This is also true for an antenna. The field in the vicinity of the antenna must deviate from the planar wave condition to fulfil the boundary conditions on the antenna surface. The concept of effective area takes this into consideration and this is why the effective area differs from the physical area.
This constraint can take some odd turns. A wire antenna, like a dipole or a Yagi antenna, will present a much larger effective area than its projected area would suggest. A parabolic reflector on the other hand will show a very obvious physical area but in this case, the effective area is smaller than the projected area.
It is now time to introduce the concept of reciprocity. A transmitting antenna that produces a certain field pattern will have an identical ‘sensitivity’ pattern when used as a receiving antenna. If we have a particular antenna with G = 10 dBi (i in dBi means 10 dB over a comparative isotropic antenna) we will in boresight have 10 dB higher power density when transmitting and a 10 dB higher output signal from the antenna when receiving a signal compared to the isotropic antenna.
So now, how is the antenna gain calculated? We can start to work with Maxwell’s equations and realize why we pay a disproportionate amount of money for a bent wire, a piece of shaped metal plate or a PCB with some seemingly haphazardly placed patches. Of course, computers and software will come to our aid, but to make a better design, a good theoretical understanding is necessary. The subject of antenna design is far beyond the basics covered in this article. However, a very simple equation can help us to understand antennas and particularly the relationship between effective antenna area, Ae, and antenna gain:

If you know either the gain or effective area then the other can be calculated and for some structures, the effective area can be closely approximated by just observing physical dimensions. The equation for Ga and Ae assumes an idealized situation where the antenna is situated in free space and is exposed to a field produced by a distant point dipole. Any perturbation of that field in the environment where the antenna is situated will affect the result.
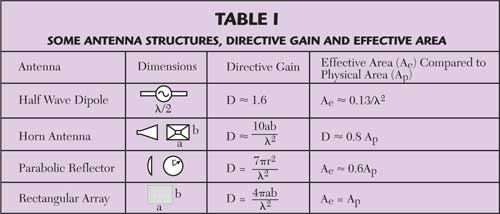
Some directive gain values for common antennas are listed in Table 1 and the effective antenna area can be calculated from those values. Note that losses are not included; hence D instead of Ga. Note also that area, Ap, in Table 1 is the physical area.
Friis equation, truth and consequence
One of the most useful equations for a telecommunication engineer can be found by combining the expression for effective area of a receiving antenna with the power density from a transmitting antenna, and calculating the apparent path loss Pr/Ptr,
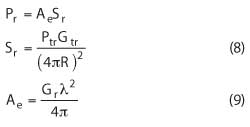
Gr = receiver antenna gain
Combining the three equations above leads to Friis equation,

Friis equation is very useful for link budget calculations; however it has sometimes been interpreted to suggest that the spatial attenuation increases with shorter wavelengths. This is not true and probably is a consequence of the embedded expression for the effective area. Friis equation assumes that the power density produced by the transmitter is constant and since Pr = Ae•Sm, the received power must vary as Ae is proportional to λ2.
The spatial dependence on wavelength is only true if the antenna gain is held constant when comparing different systems but is there any reason to keep the antenna gain constant? A constant antenna gain requires the effective antenna area to vary with the wavelength as

Figure 6 Antenna size for different wavelengths. Antenna area scales in principle with wavelength for circular symmetric antenna diagrams.
Consequently the effective area, Ae, must be decreased for a constant gain as the frequency is increased (see Figure 6). This is actually a benefit with higher frequencies since the aim is to have as small and yet as efficient antennas as possible.
In Friis equations, the antenna gain is kept constant but it is particularly important to keep the ratio between transmitter power and received signal constant and let the antenna size vary. As an example and for convenience let us consider a symmetrical link setup, with the same antenna used for transmitting and receiving. By using the relationship between effective area and gain and modifying Friis equation, we get
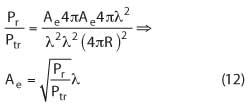
and since we want 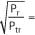 a constant and equal for all frequencies, Ae is kept proportional to the wavelength, λ.
a constant and equal for all frequencies, Ae is kept proportional to the wavelength, λ.
This is actually what we are looking for: The antenna area can be allowed to decrease linearly with the inverse of the used frequency and provide the same system link budget regardless of frequency used (This assertion overlooks the actual path loss that is present from absorption, foliage blockage, etc. All effects must be included and the atmospheric absorption can be quite high at certain frequency bands such as 24 and 60 GHz).
Parabolic reflectors
Parabolic reflectors are popular for radio links and a typical parabolic reflector antenna with a diameter, d, may have an aperture efficiency of 60 percent and thus the effective area can be expressed as

where k is a factor depending on antenna physical constraints in comparison to wavelength, but to a good approximation can be set to 0.4.
Now, if we compare two systems working at different frequencies but let the antenna size (diameter, d) be proportional to the square root of the wavelength, 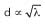 , then the effective area will be proportional to the wavelength and as mentioned above, we will find that the ratio between received power and transmitted power will always be equal regardless of frequency used.
, then the effective area will be proportional to the wavelength and as mentioned above, we will find that the ratio between received power and transmitted power will always be equal regardless of frequency used.
Example: Compare a link at 15 GHz to a link at 80 GHz with equal transmitter power. The space loss will be equal in both cases. To get the total loss between transmitter and receiver, atmospheric attenuation and other contributions must be added or compensated for.
Assume that the antenna gain for the 15 GHz link is 36 dBi, and is the same for transmitter and receiver. The equations above yield

The antenna diameter for the 15 GHz link is thus
d15 = 0.56 m
If the antennas for the 80 GHz system are scaled proportionally to the square root of the wavelengths, the antenna diameter will be

d80 = 0.24 m
Less than half the diameter compared to the 15 GHz antenna, and yet the same link budget is attained. Also note that the antenna gain will be proportional to the inverse of the wavelength, or in this case,

and consequently the antenna gain at 80 GHz will be 43.3 dBi.
However, the atmospheric attenuation must be added at roughly 2 dB/km higher for 80 GHz compared to 15 GHz. If we assume a distance of 3 km between transmitter and receiver, the 80 GHz transmit and receive antennas must each have an additional 3 dB gain to compensate for attenuation, i.e., a total antenna gain of 46.3 dBi.
The antenna diameter will then be
d80 = 0.34 m
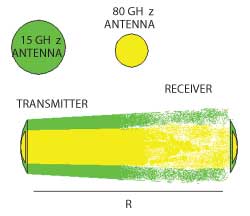
Figure 7 Relative size between 15 and 80 GHz antennas for equal link budget levels.
Comparing the beamwidth for the two cases, 15 GHz and 80 GHz using the approximate formula given earlier (see Figure 7),
bw15GHz = 3.2°
bw80GHz = 1°
Conclusion
This article has very briefly described some concepts that are well known, but are well worth further examination. One example is Friis equation that sometimes leads to the misinterpretation that radiation loss is higher for higher frequencies. This is due to the ‘free space loss’ termλ2/(4πR2) – a strange designation, especially in a lossless medium.
With the aid of a few simple equations, it is shown that millimeter-wave frequencies can offer significantly smaller antennas without any sacrifice in link budget performance. And if the benefits of superior bandwidth and lower cost for licensing are added, millimeter-wave radio is a very attractive alternative for fixed access service.
Christer Stoij received his BSEE in 1975 and MSEE 1981 from Chalmers University of Technology. He has been active in the microwave field throughout his career, since starting with Ericsson AB, and he has cofounded and founded several microwave companies including Microsystemgruppen AB and Gigatec AB. Stoij has been with Sivers IMA AB since 2000 in leading positions, and is currently acting as CTO. He remains active in engineering and is involved in design and research work in many product areas with special interest in electromagnetics, filters and structures.
