The finite element method (FEM) has been widely adopted as an analysis and design tool in many electrical engineering disciplines such as antennas, microwave and signal integrity. An FEM solver offers several important advantages over other numerical methods, including method of moments (MoM) or finite difference time domain (FDTD). These advantages include: 1) the ability to handle complex heterogeneous and anisotropic materials; 2) accurate representation of complicated geometries via tetrahedral elements; 3) accuracy through use of higher order basis functions; and 4) the ability to model with a large variety of port and incident wave excitations. With these capabilities, FEM is able to model waveguide structures with a great degree of accuracy.
However, for unbounded exterior problems, such as an antenna radiating in free space, FEM solvers require truncation of an infinite domain to a finite domain through prescribing radiating boundary conditions (RBC) on artificial truncation surfaces. Two widely used RBCs are the first-order absorbing boundary condition (ABC)1 and the perfectly matched layer (PML),2 which typically offers the best accuracy. Both techniques preserve the sparse nature of the FEM system matrix, but are only applicable on convex radiation surfaces. Both are approximate methods with resulting accuracy issues, namely spurious non-physical reflections from the radiation surfaces. This problem can be minimized with the RBC being placed further away from the radiating structure resulting in negligible reflection.
On the other hand, integral equation (IE) methods, such as MoM, are preferred for modeling geometries residing in a homogenous bounded or unbounded medium. Its analytic kernel, the Green’s function, takes into account Sommerfeld’s radiation condition at infinity. Thus, for multiple disjoint homogenous structures separated in distance, an IE solver provides a much better alternative, both in terms of memory and CPU time, since it does not require explicit modeling of the air regions between targets.
Hybridization of FEM and IE solvers was accomplished as far back as 1990 by Yuan.3 This formulation is now commonly known as the hybrid finite element and boundary integral method (FEBI), where the boundary integral (BI), a MoM solution for Sommerfeld’s radiation condition, is used as a truncation boundary for the FEM solution. By doing so, an exact theoretical treatment of the far field radiation condition is satisfied. From this a number of interesting features arise, such as radiation surfaces of arbitrary, closely spaced conformal shapes.
In this article, a novel FEBI solver, now available in HFSS from ANSYS Inc., will be presented. The solver is inspired by recent advances in domain decomposition methods. In the present FEBI formulation, an infinite unknown domain is partitioned into two non-overlapping domains: one bounded FEM domain and one unbounded homogenous exterior region. The coupling of these two domains is taken into account through an appropriate boundary condition at the interface.

Figure 1 Domain decomposition of problem domain into FEM and IE domains.
Domain Decomposition-Based FEBI Solver
The FEBI solver begins by partitioning the original problem domain Ω into two non-overlapping sub-domains Ω1 and Ω2, as shown in Figure 1.

The common interface between Ω1 and Ω2 is denoted as ∂Ω1 in the FEM domain and ∂Ω2 in the IE domain. This distinction is necessary because the present formulation allows non-conformal coupling between two domains; namely, meshing, basis function and basis order, matrix assembling and solution process of each domain can be treated independently. The ability to handle different basis orders in a modular fashion for each domain is of vital importance for a robust FEBI solver, because higher order IE solvers are still on-going research topics.
Based on domain decomposition, the final system matrix can be written as

where AFE and ABI represent the system matrices of FEM and BI domains, respectively. C is the coupling matrix between the two domains. The coupling is done only through electric and magnetic currents at the interface; thus, it is very sparse. The solution of Equation 2 is accomplished iteratively via splitting

leading to
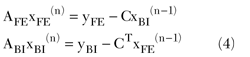
The benefits of using a domain decomposition approach are apparent from Equation 4. The FEM and BI domains are decoupled; thus, parallelization becomes trivial. The preceding description shows that BI can be used as an exact termination condition in FEM; due to the implementation’s modularity, state-of-the-art FEM and IE solvers are easily employed.
Applications
In this section, two examples of this hybrid method will be used to highlight the advantages of FEBI. As mentioned previously, the first order ABC can be placed on a sufficiently spaced bounding region that is conformal, but may not be concave. On the other hand, PMLs can be placed closer to the model, but are most easily applied to a rectangular bounding region. For the hybrid FEBI technique—since the coupling between the electric and magnetic currents on the boundary are accurately computed—these shape and size restrictions do not apply. Testing of this new boundary has shown that a spacing of λ0/10 provides the optimal compromise between speed and problem size,5 where λ0 is the wavelength in free space. In addition, the FEBI boundary can be highly conformal, including concave regions. It is also possible to enclose individual parts of the model in separate domains, each with a BI boundary. By using highly conformal and separate air regions, one can significantly reduce the size of the finite element problem region, resulting in a highly efficient simulation. To illustrate this, let us consider two examples: one using separate volumes and one utilizing a highly conformal boundary surface.

Figure 2 Dielectric lens with rectangular feed horn.
For the first example, the textbook model of a dielectric lens6 is considered. The lens and its feed horn are shown in the inset of Figure 2. The lens focuses the fields from the source antenna in the forward direction. The lens simulated here with a rectangular waveguide as a feed has an εr = 2.56 and a front face with a diameter of 4.4λ0. A hybrid FEBI was used to model this system using separate air regions with a rectangular air region placed around the feed horn and a conical air volume around the lens. A BI boundary was applied to the bounding surface of both volumes.

Figure 3 Radiation pattern for the lens.
For comparison, this antenna system was also modeled using PMLs, where the surrounding air region is a larger rectangular air box that encloses the entire model with sufficient spacing to ensure an accurate response. Using the smaller air volumes in the FEBI model reduced the memory usage by a factor of 10, when compared to the PML simulation. Shade plots of the computed electric fields from the two simulations are shown in the figure. As illustrated, despite using smaller separate air volumes in the FEBI simulation, the fields computed in and around the lens and horn are accurate and agree with fields calculated using the PML. The reflection coefficient (Γ) of the horn is increased when placed near the lens. Both the FEBI and the PML simulations show an identical increase in Γ of 1.8 dB, when compared to the input response for the isolated horn. The pattern in the forward direction for this antenna system computed using both procedures is shown in Figure 3. Once again, the agreement between the FEBI and PML is excellent. The plots in Figures 2 and 3 show the accuracy of the FEBI for characterizing the response of an antenna system, when using separate air volumes.

Figure 4 Array of helical antennas mounted on a satellite.
For the second example, an antenna array mounted on a complex platform is considered. This model is shown in Figure 4. It is a seven-element array of helical antennas that are mounted on a satellite platform. The length of the satellite from end to end is 18 feet and the antennas are characterized at 3.5 GHz. This is a large model and so the domain decomposition method (DDM) was also used to split the FEM domain into several smaller domains.7 This integrated antenna platform system was previously simulated using a standard ABC, with a large enclosing rectangular air box.5 The volume enclosed in the surrounding air box for that model is ≈ 21000 λ3; the DDM was used to distribute the solution over 34 domains. The total memory needed for the simulation was 210 GB of RAM.

Figure 5 Radiation pattern for the antenna array mounted on the satellite.

Figure 6 3D polar plot of radiated fields for the seven-element array with equal excitation.
For the FEBI simulation, a highly conformal air volume was used. This conformal air volume is shown in the inset. This air volume encloses a much reduced 1200λ3. With this reduced air region and the DDM applied over 12 domains, the simulation required 21 GB of RAM. The memory needed for a FEBI simulation was reduced by an order of magnitude over a solution using a standard RBC. The radiation patterns for all antenna elements excited with equal amplitude and phase from the two simulations are compared in Figure 5. There is an excellent agreement between the two patterns. The full 3D polar pattern for the equally excited antenna array on the satellite simulated using the FEBI is shown in Figure 6. From this example, it can be seen that, by using the FEBI with highly conformal bounding regions, one can simulate large complex antenna systems on a single desktop computer.
Conclusion
The hybrid FEBI is a powerful new enhancement to the FEM solver available in HFSS. This new technique gives the design engineer the advantages of an FEM simulation with the efficiency and accuracy of an IE solution for open boundary problems. This procedure is accurate for conformal, concave and/or separate air volumes, allowing users to reduce the size of the FEM solution region resulting in a significant reduction in the solution time and the amount of memory required to solve the problem.
References
- J. Jin, The Finite Element Method in Electromagnetics, Second Edition, John Wiley & Sons Inc., New York, NY, 2002.
- Z.S. Sacks, D.M. Kingsland, R. Lee and J.F. Lee, “A Perfectly Matched Anisotropic Absorber for Use as an Absorbing Boundary Condition,” IEEE Transactions on Antennas and Propagation, Vol. 43, No. 12, December 1995, pp. 1460-1463.
- X. Yuan, “Three-dimensional Electromagnetic Scattering from Inhomogeneous Objects by the Hybrid Moment and Finite Element Method,” IEEE Transactions on Microwave Theory and Techniques, Vol. 38, No. 8, August 1990, pp. 1053-1058.
- M.N. Vouvakis, S.C. Lee, K. Zhao and J.F. Lee, “A Symmetric FEM-IE Formulation with a Single-level IE-QR Algorithm for Solving Electromagnetic Radiation and Scattering Problems,” IEEE Transactions on Antennas and Propagation, Vol. 52, No. 11, November 2004, pp. 3060-3070.
- A. Sligar, ”HFSS 13: Hybrid FE-BI for Efficient Simulation of Radiation and Scattering,” presented at Ansys Users Group Meeting, October 2010.
- R.E. Collin, Antennas and Radio Wave Propagation, McGraw-Hill, New York, NY, 1985.
- J. Silvestro and M. Commens, “HPC Options for HFSS,” Ansys Advantage, November 2010.
