S-parameters have been used to represent linear networks for simulation and design since the 1960s. Measuring S-parameters was made possible with the introduction of the network analyzer. Designers could then integrate S-parameter "black-boxes" along with other electrical components using linear frequency-domain simulators. The measure, model and simulate triumvirate has proven quite successful for high frequency electronic design of linear devices. Unfortunately, the nonlinear behavior of high-frequency semiconductor devices cannot be represented by S-parameters. Nonlinear device characterization has always been challenging and limited. To better serve designers, test equipment manufacturers, software providers and integrated device manufacturers would like to offer similar black-box characterization for nonlinear devices.
Over the past two decades, developments in nonlinear measurement, modeling and simulation have been introduced in literature. This past year, Microwave Journal and others have published numerous articles describing products based on these efforts. In this article, we take a glimpse at the history of development, what is currently available, and how the future of nonlinear characterization/simulation and the microwave electronics industry are intertwined.
Why Change is Happening
Nonlinear devices perform critical functions from frequency conversion to signal amplification. Under large-signal drive conditions, they distort waveforms (time domain) or generate harmonics, inter-modulation and spectral re-growth (frequency domain). Sometimes the behavior is exploited, as in the case of a mixer or frequency doubler; sometimes it must be managed, as in the case of a linear amplifier.
Market demands for more bandwidthódriven by the explosive growth of social media and smart phonesóalong with the desire to reduce telecommunicationís carbon footprint is forcing our industry to deliver products that are more linear (to increase capacity) and efficient (to lower power consumption). As these demands become more stringent, the industry faces an inflection point as to how to reach these goals. What is the most efficient way to capture, portray and address nonlinear behavior in the design process?
Representing Nonlinear Devices
Microwave electronics are developed through a variety of ìcustomî modeling/design methods. Currently, the more common approaches include:
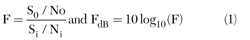
1. Empirical and Physics-based compact models such as Materka, Curtice Cubic, or Gummel-Poon use physical knowledge of the device and an array of measured data such as S-parameters and current-voltage (I/V) data (DC and pulsed). Model parameters are empirically adjusted to fit this measured data, extracting the model parameter values that replicate the device response to given stimuli. A data file of these parameters is generated by the modeling team and delivered to the designer for use with the appropriate circuit simulation model. The extracted compact model aims to provide a reasonably accurate representation of the device, which is scalable (i.e. transistor size/gate periphery) and applicable for the intended operating range.
New transistor technologies and demand for greater accuracy leads to an increase in device and model complexity, driving the need for enhanced characterization techniques and specialized test equipment. New model development can take years and often requires the skills of PhD level technologists. Their expertise is needed to ensure that the model adequately predicts behavior for the intended application and that the measurement system itself does not introduce errors. Good models are expensive to develop, contain sensitive device information and are often proprietary. Such models do not address larger networks, such as an RFIC functional block. For that, a detailed circuit block or behavioral model is needed.

2. Load-pull measures figures of merits (FOM) such as output power or power-added efficiency versus the load or source impedance. The data is collated into constant performance contours on a Smith chart, providing the impedance target for a matching structure. Since no device model is developed, sensitive device information is protected and parameter extraction is no longer required. While easier to obtain than compact models, load-pull information limits the understanding of device performance to specific metrics, test conditions and device criteria (gate periphery, bias, packaging). A change to any of these invalidates the load-pull information. Fortunately, automation in load-pull systems makes additional tests a viable solution for a reasonable number of operating variables. As a direct design tool, active harmonic load-pull systems can overcome losses between the load and device and provide independent control of impedance values at harmonic frequencies in order to achieve optimum device performance in the lab. Furthermore, load-pull plays an important role in the efforts to develop the measurement-based black-box models described below.
3. Lastly, designers may use a hybrid of S-parameters, load-pull and behavioral models based on nonlinear FOMs such as conversion gain, saturated power, the 1 dB compression point, two-tone third-order intercept point, etc. This method is most common in system development where block integration is the main focus and critical impedance matching will occur at the circuit level using one of the approaches mentioned previously.
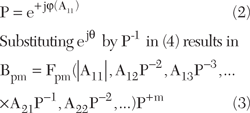
Nonlinear behavioral models do have some noteworthy limitations. For instance, they only work in the forward direction, might only assume a single tone input, and may not account for impedance mismatch at the device ports. This leads to unacceptable simulation errors when cascading nonlinear devices, like mixers and amplifiers. In addition, these behavioral models require multiple instruments and configurations to obtain the various FOMs that define them. To streamline the design process, a measurement-based nonlinear behavioral model would have to overcome these FOM behavioral model inaccuracies. It would also need to be easily extracted from a single measurement system developed to generate such a model for the intended software simulation environment.
Due to the complexity, lead time and cost of developing a compact model, the limited information offered by load-pull and FOM black-boxes, technologists have been pursuing an alternative that is easier to implement, sufficiently generalized and provides reliable accuracy. The effort to develop measurement-based nonlinear black-boxes, similar to S-parameters, dates back to the late 1980s and early '90s.

The Challenge of Nonlinear Characterization
A key issue for nonlinear measurements is that they do not simply scale with the stimulus. Unlike the microwave network analyzer, which measures the ratio between the stimulus and the response in order to characterize the linear DUT, a large-signal VNA must measure absolute values in order to fully represent nonlinear DUT behavior. The response is often at a different frequency than the stimulus.
Measured nonlinear behavior can be expressed by a series of equations in time or frequency domain using voltages/currents or waves. The voltage-current or wave combination at all ports define the state of the device in a unique way. If one performed an infinite number of measurements by changing the environment (i.e. power levels, biases, load impedances, etc.), the resulting infinite table of realizations would describe this device completely. Clearly, this is not an option. However, performing a limited set of experiments, which then can be interpolated with confidence, is practical. Such a model would be valid within a well defined set of operating conditions, including the excitation signals.1 This ìmeasurement basedî black-box would offer certain benefits over the compact model, load-pull or FOM behavioral models. Such a model could accurately replicate the signal distortion currently addressed by compact models, without the intensive extraction process. It would only require that the black-box was obtained with a measurement system under similar conditions as the intended application, calling for closer collaboration between characterization and design.

Early Nonlinear Efforts
Hewlett-Packard (now Agilent) began research in nonlinear modeling and measurement technology back in the ë90s. In 1990, the company started a small research group called the ìHP - Network Measurement and Description Groupî†or HP-NMDG. The group, which included J. Verspecht, E. Van Damme, F. Verbeyst and M. Vanden Bossche (who was finishing his PhD thesis on ìMeasuring Nonlinear Systems: A Black-box Approach for Instrument Implementationî with sponsorship from HP), was tasked with developing a nonlinear network measurement system (NNMS). Initial efforts were on extending S-parameters to weakly nonlinear devices using Volterra series (VIOMAP). Over the years internal HP prototypes were given different names when presented at conferences or industry tradeshows including the Vector Nonlinear Network Analyzer (VNNA) and the Large-Signal Network Analyzer (LSNA).2
The Poly-harmonic Distortion Model
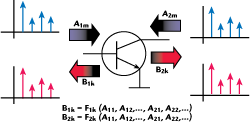
Limitations of the VIOMAP approach led to new modeling efforts by HP through Jan Verspecht and David Root in the early 1990s. HP funded Verspechtís PhD work at the University of Brussels (VUB) on a multi-frequency ìDescribing Functionî concept to address the limitations of the Volterra theory in accurately describing ìhard nonlinearî behavior (see Figure 1). Unlike the Volterra theory, this new mathematical framework described very hard nonlinear behavior as encountered in comparators, harmonic mixers, samplers and other hard clipping devices.3 The DUT could be represented by a spectral mapping function, Fpm (1) that correlates all of the relevant input spectral components Aqn with the output spectral components Bpm, whereby q and p range from one to the number of signal ports and whereby m and n range from zero to the highest harmonic index.4

These efforts ultimately led to the Poly-harmonic Distortion (PHD) modeling approach, which is the basis for todayís commercial nonlinear measurements, modeling and simulation. In June 2003 Marc Vanden Bossche would leave HP/Agilent and created a separate company, Network Measurement and Description Group (NMDG). NMDG continued developing a software architecture and framework called the Integrated Component Characterization Environment (ICE) and S-function models. Agilent continued its research and investment on PHD modeling. In 2005, Agilentís Loren Betts began research into the nonlinear measurement and modeling problem while pursuing his Agilent-sponsored PhD through the University of Leeds (UK) under Professor Roger Pollard.6 Bettís PhD research brought him together with Verspecht and Root, whose combined work, along with others at Agilent, led to enhancements to the PHD modeling approach and ultimately the X-parameter model and the Nonlinear Vector Network Analyzer (NVNA) on the Agilent PNA-X platform.
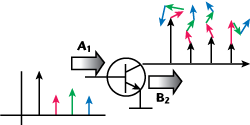
Meanwhile, other companies have also used the PHD modeling approach as a starting point including NMDGís S-functions. Basically the approach defines mappings of the input signal to the spectral components appearing at all the device ports, generated by device nonlinearity. Under nonlinear operating conditions, the superposition principle is not valid. However, in many practical cases, such as a power amplifier stimulated with a narrowband input signal, there is only one dominant large-signal input component present (A11) whereas all other input components (the harmonic frequencies) are relatively small. In that case, the harmonic superposition principle for the relatively small input components can be applied, as illustrated in Figure 2. During the measurement, several small-signal tones that are harmonically related to the fundamental drive are used to perturb the device under test at each large-signal state. These small perturbation tones are injected at ALL the terminals of the device in turn and at each harmonic of the fundamental drive. The harmonic superposition principle asserts that the magnitude of the small test signals is such that the perturbation can be viewed as a linear process analogous to mixer theory whereby only the LO signal is large enough to bring a nonlinear device into a time dependent linear operating mode.

By introducing a complex phase reference point (2) set by the phase of the large-signal A11, the spectral mapping function of (1) can be re-written as (3) so that the mapping between input and output is time invariant.
A linearization of this equation results in a PHD model (4).
The basic PHD model equation (4) simply describes that the B-waves result from a linear mapping of the A-waves, similar to classic S-parameters. That the right-hand side of (1) contains a contribution associated with the A-waves as well as the conjugate of the A-waves is significantly different from S-parameters, where the conjugate part is not present at all. That is the case since, with S-parameters, the contribution of an A-wave to a particular B-wave is not a function of the phase of that A-wave. Any phase shift in A will just result in the same phase shift of the contribution to the particular B-wave. This is no longer the case, however, when a large fundamental signal (A11 wave) is present at the input of a nonlinear DUT. In that case, the large-signal A11 wave creates a phase reference point for all other incident A-waves, and the contribution to the B-waves of a particular A-wave depends on the phase relationship between this particular A-wave and the large-signal A11 wave.4
The PHD modeling approach requires nonlinear measurement systems that can capture the absolute amplitude of signals at the ports of a device as well as the relative phase between frequency components. This information is necessary to study the phase of the distortion and ultimately the nonlinear behavior of the DUT. Therefore, new measurement systems had to be developed to generate the model.
Milestones in Nonlinear Measurement Development
Measuring nonlinearity in the time or frequency domain is driven largely by the state of technology. Measurement systems have used a variety of instruments, including oscilloscopes (both real-time and sampling), vector signal analyzers (VSA), real-time signal analyzers (RTSA), large-signal network analyzers (LSNA) and nonlinear vector network analyzers (NVNA) based on VNAs. Different architectures capture signal distortion through a variety of techniques. Frequency based solutions must maintain or reconstruct the phase relationships between frequency components to achieve faithful waveform representation. If the instrument measures multiple port devices, the phase relationships between signals measured at each port must be maintained as well.
Since a nonlinear DUT creates additional spectral components different from those applied at the input, characterizing a nonlinear device requires an instrument that can measure this complete spectrum in a single measurement take. This is not possible with the ìheterodyneî measurements of standard linear network analyzers where the device response is obtained through successive excitation at one single spectral point. A fast way to reuse the ìheterodyneî principle was first proposed by Urs Lott.
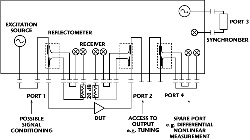
In 1989, Lott published ìMeasurement of Magnitude and Phase of Harmonics Generated in Nonlinear Microwave Two-ports.î7 The technique successively measured each harmonic generated by the nonlinear DUT (excited by a pure sine wave) by synchronizing the linear VNA to the corresponding harmonics generated by an auxiliary generator, which was phase coherent with the excitation source (see Figure 3). A known ìgolden standardî diode was used as a phase reference to calibrate phase errors. A major drawback of this initial approach was the assumption that the input signal was a spectrally pure sine wave. This is not often the case since nonlinear microwave systems often distort the input signal through source-pull resulting in the presence of harmonic excitation components on the incident wave of the DUT.8 Future developments would address this source of error and much of Lottís initial concepts are found in nonlinear network analyzers today.
Other early nonlinear measurement systems included that of M. Sipil‰, K. Lehtinen, V. Porra9 in 1988 and G. Kompa and F. van Raay10 in 1990 (see Figure 4). Both efforts were based on microwave digitizers using digitizing sampling oscilloscopes (DSO) to measure the fast RF time domain waveforms by an equivalent time sampling. Kompa, et al extended the set-up of Sipil‰, et al with the use of a VNA to calibrate the test set. Two switches directed the REF and TEST signals to either the broadband sampling oscilloscope (triggered by the fundamental) used to measure the harmonics coherently, or to the network analyzer used to measure the fundamental behavior and calibrate the system. This configuration provided greater accuracy through the VNA calibration and addressed the trigger drift problem. But it was still slow, vulnerable to phase distortion errors introduced by the oscilloscope sampling heads and limited to one port excitation (DUT input).
The calibration procedure used by Kompa, et al and Demmler, et al took into account the phase distortion of the transition analyzer, applying an analog to Lottís approach of using a ìreference generatorî to precisely obtain the phase relationship between fundamental and harmonic tones.8 The development of a traceable harmonic phase calibration process was the enabling technology for all subsequent NVNA work. In the mid-í90s, researchers at NIST measuring the phase dispersion of a broadband receiver developed an ingenious electro-optic sampling set-up capable of characterizing harmonic phases up to 100 GHz with a NIST-traceable error of less than one degree.11 All the harmonic phase standards used in todayís NVNAs are traceable to this set-up.
HP built its first LSNA prototype in 1992 based on four couplers to detect the incident and scattered waves at both ports using a 20 GHz bandwidth sampling oscilloscope for the data acquisition. Requiring a few hours to calibrate and about three minutes for each data acquisition, this prototype was much too slow for practical use. It also had trigger drifting problems. A faster solution was found in 1993 by replacing the oscilloscope with a sampler-based instrument leveraged from two HP Microwave Transition Analyzers, a commercial instrument introduced in 1991. With four fully synchronized RF data acquisition channels, it supported the phase and amplitude measurements of the fundamental and harmonics at both input channels for frequencies up to 40 GHz. Since it was based on the harmonic mixing principle, rather than on equivalent time sampling, the instrument allowed data acquisition about 100 times faster than what was possible with a sampling oscilloscope for the same or even a better dynamic range (typically better than 50 dB).2
By 1995, HP used high-precision analog-to-digital convertors to replace the MTAís internal ones, resulting in a somewhat faster instrument with more dynamic range and increased linearity. In 2003, Agilent licensed the LSNA IP to Maury Microwave who continued to offer this sampler-based architecture. Agilent continued nonlinear research with a mixer-based architecture, which resulted in an early nonlinear vector network analyzer (NVNA) prototype based on the Agilent PNA-L in 2005.6
Using microwave transition analyzers for signal detection was also being pursued by Demmler, Tasker and Schlechtweg at essentially the same time (1994). Professor Tasker and others at Cardiff University developed the table-based Cardiff model and its associated measurement system. Unlike the PHD modeling approach, which is based on amplitude/phase information of a DUTís spectral response, the Cardiff measurement system captures the current/voltage waveform at the device ports with a test set-up based on a sampling oscilloscope. The resulting model uses four table-based nonlinear functions: Ic, Qc, Vbe and Qb, all defined versus Ib and Vce (based on a non-uniform bias grid) to define device behavior for a given input stimulus, bias and terminating impedance. The system can employ single or multiple-tone large-signal measurements including harmonic load-pull. The look-up table approach forces the designer to stay within the ëmeasurement spaceí to avoid extrapolation errors.12
Commercial Nonlinear Measurement Systems
The following is a brief description of the various large-signal or nonlinear vector network analyzers, time-sampling oscilloscope-based systems, and load-/source-pull systems available today.
Agilent Technologies and Partners
Agilent continued nonlinear research with a mixer-based architecture, which resulted in an early nonlinear vector network analyzer (NVNA) prototype based on the Agilent PNA-L in 2005.6 Today, Agilentís PNA firmware transforms the linear vector network analyzer into an NVNA to measure the vector corrected absolute amplitude and cross-frequency phase stimulus/response of a device. A new Agilent phase reference, based on an active IC, provided the capability to measure the vector corrected cross-frequency phase out to 50 GHz with very narrow grid spacing. Since the amplitude and cross-frequency phase of all the frequency spectra is accurately known, an inverse Fourier transform can be applied to the frequency domain data to generate the time domain waveforms.
These vector corrected stimulus/response measurements lay the foundation for the automated X-parameter measurements. Figure 5 illustrates the PNA-X mixer-based NVNA architecture. Since the X-parameter measurements for a two-port component require two sources, the PNA-X hardware architecture utilizes integrated, ìspectrally pureî sources, internal combining network, internal pulse modulators/generators, and flexible signal routing.
The NVNA can be used as a vector corrected time domain scope by measuring the absolute amplitude and cross-frequency phase of the signals with error correction applied. The NVNA with the N5244A PNA-X can sweep from 10 MHz to 50 GHz creating a time domain scope with 50 GHz of detection bandwidth for a discrete point resolution of 1/(50 GHz) ≈ 20 ps. This time domain data can be used to examine the I/V waveforms at the device terminals in order to analyze the linear and nonlinear characteristics of a component. The RF I/V curves can be superimposed on the DC I/V curves providing the designer important information on the component behavior under various DC bias and RF conditions.
The Agilent instrument can also measure the multi-tone and inter-modulation products at the fundamental and harmonic frequencies. The NVNA can be used to analyze complex signals such as those present with a device operating under fast RF and/or DC pulses. To measure and analyze memory effects, a multi-envelope measurement can be performed where the component is stimulated with a pulsed signal (RF and/or DC bias) and the resulting envelope ëaí and ëbí waveforms are measured at the fundamental and harmonics frequencies. The envelope amplitude and phase can be analyzed versus time at each of the spectral components. More recently, the NVNAís measurements were extended to include dynamic envelopes resulting in the new multi-envelope measurement domain.13 The multi-envelope measurement domain is currently being utilized to measure X-parametersô with enhanced time-varying dynamics.
Agilent along with Maury Microwave extended the X-parameter measurement capability by adding arbitrary load-dependence X-parameters (fundamental and harmonic frequencies) to the NVNA. This capability has also been extended to the load-pull system from Focus Microwave. The full, complex Gamma dependence of a device under large-signal operating conditions is captured and can be exported into simulation software allowing devices to be accurately represented using X-parameter models in cascaded multi-stage, Doherty or other complex amplifier circuit simulations. Additionally, the load-pull option lets researchers account for arbitrary load mismatches, measure dynamic load-lines and optimize performance. The system does not currently support direct independent control of harmonic impedances; however, the uncontrolled harmonic impedances presented by the load tuner are captured through calibrated measurements and corrected for in the exported X-parameters. Although the system itself does not support optimization through harmonic tuning on the test bench, the information captured in the X-parameters enables performance optimization via harmonic tuning during simulation.
Mesuro/Tektronix
An alternative measurement/modeling approach is offered by Mesuro Ltd., a commercial entity with ties to the longstanding developments taking place at Cardiff University (Tasker, Benedikt, et al). Their ìwaveform engineeringî measurement system includes a test set similar to the VNA and a sampling oscilloscope instead of samplers or mixers. The system (MB20 and MB150) can optimize performance directly on the test bench via active harmonic tuning and generate a measurement-based model.
The measurement solution enables emulation of realistic signal conditions at the DUT. Calibration ìremovesî the package or test fixture behavior, placing the measurement reference plane directly at the DUT ports. Designers gain direct access to current and voltage waveforms to study their shape and optimize the device performance through control of the harmonic impedances at the device ports. For the case of designing a single-stage amplifier, the benefit to waveform engineering is that real-time visualization and control of I/V waveforms at the device terminals will give the engineer a big advantage in determining what (load) makes the device work best at the time of the measurement rather than by capturing its behavior as a black-box and optimizing the performance during simulation. Independent control of harmonic impedances is critical to optimizing performance through waveform engineering. For design work that goes beyond a single DUT, such as a multi-stage amplifier, a simulation model is still required. For these instances, the Mesuro system can produce the I/V table-based model that was developed at Cardiff University.
The system modules include the following: A wideband receiver based on a Tektronix sampling oscilloscope capable of simultaneously capturing all signal components from DC to 67 GHz with effective 12 bit accuracy and a dynamic range of up to 50 dB; an arbitrary waveform generator (also from Tektronix) that synthesizes fully synchronous waveform shapes for the input and output of the DUT up to 6 GHz, when using both outputs separately, or up to 10 GHz in interleave mode; an RF and baseband test-set that allows for the contactless detection of the current and voltage waveforms and an interface with the active source and load-pull system while providing bias to the DUT; and integrated software tools for calibration, measurement, waveform analysis and control of the system including active harmonic load-pull.
The use of an oscilloscope provides a measurement whose speed is fixed, regardless of the complexity of the signal. These instruments measure over a broad bandwidth and are not limited to acquisition around harmonics of the excitation. There is, however, a corresponding reduction in dynamic range when compared to systems based on harmonic mixing or ìsampling downconversionî techniques. The measurement accuracy of the oscilloscope can also be affected by both time-base distortion and jitter, although these can be corrected using methods to compensate for random and systematic timing errors, as described in Reference 11.
NMDG, Rohde & Schwarz, Maury Microwave and Focus Microwave
Starting in 2003, Maury Microwave and NMDG worked together on the first commercially available large-signal network analyzer, the MT4463. This Maury/NMDG LSNA, using technology licensed to Maury by Agilent Technologies, was configured largely from Agilent test equipment and NMDG developed hardware/software. It was released in March 2005 and measured the complete voltage and current or incident/reflected wave behavior under small- (S-parameters) and large-signal conditions.
Since June 2008, NMDG has partnered with Rohde & Schwarz to enable its VNAs with the ability to characterize nonlinear devices in time and frequency domains. NMDGís NM300 ZVxPlus (see Figure 6) is a combination of software and hardware that runs on top of the Rohde & Schwarz ZVA and ZVT series Vector Network Analyzers (VNA), supporting a frequency range from 600 MHz up to 20 GHz. The measurement system can be calibrated to measure the incident and reflected waves or voltages and currents at the ports of a component under test, under realistic conditions using a periodic harmonic-related stimulus and supports analysis of nonlinear harmonic behavior in the frequency domain, harmonic measurements including phase, fundamental and harmonic tuning, time domain representation and non 50 ohm measurements.
The R&S VNA features independent synthesizers to support measurements on amplifiers and frequency-converting DUTs such as mixers and front-ends. The high spectral purity of the source signals as well as the high intercept point and high sensitivity of the receivers eliminate the need for external filters in multi-tone measurements and measurements on frequency-converting DUTs. Rhode & Schwarz ZVA can also be used to perform hot-S22 measurements.
NMDG is also partnered with Focus Microwaves, extending their solution to include fundamental and multi-harmonic source- and load-pull systems utilizing computer controlled electro-mechanical wideband and harmonic tuners with VSWR performance ranging from 10:1 to over 200:1.
Anritsu/HFE
Anritsuís VectorStar Nonlinear System stems from collaboration between Anritsu and High Frequency Engineering Sagl of Switzerland (HFE). The system includes an HFE test set, various components for load-pull analysis and the HFE software. Anritsuís MS4640A family of VNAs can control as many as four independent signal sources for multi-tone measurements and direct-access loops for source and receiver monitoring. Applications include built-in programmable power sweeps for gain-compression analysis at multiple frequency points, inter-modulation distortion (IMD) measurements and harmonic measurements.
The Anritsu/HFE nonlinear system inserts a low-loss coupler between the DUT and load-pull tuner, achieving improved measurement accuracy of the source and load impedances at the DUT. This approach makes it possible to monitor the impedance in real time while also monitoring the performance of the DUT. The VNA provides immediate display of the DUTís performance in response to changes in impedance, allowing real-time tuning. Pre-calibrated tuners are not required since the impedance can be monitored while the DUT is being measured. This configuration also eliminates the importance of tuner repeatability. The Anritsu/HFE active loop tuner is capable of providing gamma values to 1.0 at the DUT port. Alternatively, any type of impedance tuner from any vendor can be used in the load-pull system.
Nonlinear data is available directly from the software in a number of formats. This solution can provide nonlinear figures of merit for use in a ìsystem-levelî behavioral block or load-pull information for designing an optimum impedance matching network in a separate EDA tool. Anritsu and HFE are exploring exportable nonlinear model formats as members of the OpenWave Forum.
AMCAD/Auriga/Modelithics/VTD/HF Technik
Started in 2004 by researchers from XLIM Laboratory in France, AMCAD provides a modeling tool with pulsed I/V RF characterization and load-pull system. Their associated software platform (IVCAD) controls these test benches, manages measured data and model extraction with direct links to RF EDA tools (ADS, MWO). They are currently among the few independent companies providing X-parameters characterization and PHD model extraction services.
Other firms offering nonlinear device characterization include Modelithics (DC and pulsed I/V, load-/source-pull, compact model and X-parameter extraction), which was founded in 2001 by Lawrence Dunleavy and Thomas Weller, and Auriga Measurements Systems LLC (DC and pulsed I/V, load-/source-pull, compact model), which was founded in 2004 by Yusuke Tajima. Auriga also manufactures and sells custom Automated Test Equipment (ATE) for device modeling.
In 2008 Jan Verspecht co-founded the company Verspecht-Teyssier-DeGroote SAS. The company, also known as VTD, uses the sampling architecture of the LSNA in order to build the SWAP-X402, an affordable measurement†instrument dedicated to the time-domain load-pull characterization of power transistors (not optimized for behavioral modeling). It has the capability to measure the phase and amplitudes of harmonics (and as such the time domain waveforms), even under pulsed operating conditions.
Heuermann HF-Technik GmbH (HHF) is a spin-off of the Aachen University of Applied Sciences. Founded in 2008 by Professor Heuermann, the companyís NonLin-S product performs calibrated complex nonlinear measurements with a multi-port-VNA from R&S, Agilent or Anritsu (ZVA, ZVB, ENA, PNA, or Anritsu). The system supports IM measurements, mixer measurements, harmonic measurements, sampling oscilloscope measurements and spectrum analyzer measurements.
Designing with Nonlinear Measurement Models
For further analysis and circuit design, the X-parameters, S-functions, Cardiff models, etc. from the measurement system (Agilent, NMDG/R&S, HFE/Anritsu and/or Tektronix/Mesuro) must operate with a simulator that supports RF/microwave models and analyses, i.e. Agilent EEsof ADS, Genesys or AWR’s Microwave Office (MWO). With four different measurement systems extracting models based upon different techniques, there is a need for a common model file format support that reaches across measurement and simulation platforms. This well-recognized need has spawned two approaches.
X-parameters
Since Agilent produces both measurement system and design software, they have developed the capabilities of both simultaneously, leading to the NVNA/X-Parameter solution. The Agilent NVNA firmware allows a user to define the saved data as A and B waves, voltages, currents, or X-parameters. The data is saved in the Microwave Data Interchange Format (MDIF), a file format initially developed for behavioral modeling of nonlinear devices in ADS, which has become a de-facto standard supported by other tools as well. In ADS, the X-parameter simulation component is a native compiled simulation element that directly interfaces with the spectral Jacobian of the nonlinear simulator and can be used with all other ADS components in a circuit design.
Agilent wants to establish X-parameters as an industry standard, publishing the equations (IEEE Explore) and the underlying X-parameter theory. According to Agilent, the files are open, documented, non-encrypted and human readable to ìenable broad industry adoption and to encourage others to join in the development of the technology.î The company asks for direct collaboration with companies interested in supporting X-parameters in order to provide updates to the standard as it evolves and ensure quality. According to Agilentís website, the company is currently providing additional support to key customers and strategic partners due to the ìrapidly developing state of the technology, as well as finite resources.î
The OpenWave Forum
Evolving concurrently alongside Agilentís X-parameters approach is the effort spawned by AWR, Anritsu, HFE, Mesuro, NMDG, Rohde & Schwarz and Tektronix last fall to form an industry alliance (www.openwave forum.org) with the goal of establishing an open standard for exchanging nonlinear behavioral modeling data across multiple vendor tools.
This group, known as the OpenWave Forum (OWF), also wishes to create and promote a unified and transparent data exchange format for large-signal nonlinear simulations, measurements and models. The yet-to-be-finalized open standard will ensure that data from any compliant measurement system would be compatible and transportable to any EDA environment that recognizes the standard. The alliance believes their collective approach is necessary to facilitate an open standard that represents a mutually agreed upon flexible, non-proprietary MDIF data format for nonlinear systems.
Simulation
Microwave nonlinear simulators such as ADS, Genesys, Microwave Office and Ansoft Designer use the Harmonic Balance algorithm, which splits the circuit/system into two sub-circuits, a linear sub-circuit and a nonlinear sub-circuit. This technique, which has been in use for decades, allows the simulator to solve the linear portion in the frequency domain and the nonlinear portion in the time domain. The time domain is required for addressing the time variant signal distortion due to device nonlinearity. The frequency domain provides a speed advantage for solving the linear portions of the network, which may include dispersive elements such as transmission lines. The nonlinear time-domain solution is converted into the frequency-domain via discrete or fast Fourier transform (DFT or FFT) and the spectra of the currents at the linear-nonlinear interface are compared. The spectra used in the algorithm is defined by the RF source (or sources) placed in the schematic to drive the DUT and the simulation set-up specified by the user and includes the number of harmonics and inter-modulation tones for the simulation engine to solve.
The continuity equation requires that the nonlinear currents equal the linear currents. The technique seeks a solution to this steady-state nonlinear problem by iteratively solving for a set of variables such as the voltages at the linear-nonlinear interface. This iterative process of ìbalancingî the currents between the linear and nonlinear network nodes can be responsible for lengthy simulation times and in certain cases, a failure to converge. This can occur when the spectral content is high (highly nonlinear conditions) or many nonlinear elements exist.
As a frequency defined device, PHD models are not solved in the time domain, obviating the Fourier transform and iterative solving of the harmonic balance algorithm. Essentially, large-signal VNAs and the PHD modeling approach do in measurements and modeling what Harmonic Balance (and Circuit Envelop) algorithms do in simulation. This results in reduced memory requirements and fast simulation run times.
Model accuracy is ensured by the fact that the PHD model is directly derived from measurements (or models derived directly from circuit simulation). The modelís accuracy holds as far as the DUT is stimulated under the conditions for which the assumed harmonic superposition principle holds. The simulation stimuli and load conditions must also reflect those of the measurement. Load dependent PHD models from load-pull measurements (or simulation) are required when the terminal impedances in the simulation are different than those of the measurement system (typically 50 ohm) as would be the case with mismatched cascaded black-boxes (i.e. multi-stage amplifier or front-end module).
Multi-tone Analysis
X-parameters are a complete description of steady-state multi-tone nonlinear component behavior. They scale with number of ports and large-signal tones. The initial X-parameter measurements on the NVNA were supported for a single large tone stimulus on a two-port device. Inferences about component behavior in response to continuous spectrum input envelope signals (digital modulation) can be made by leveraging the AM-AM and AM-PM information in the one-tone X-parameters using circuit envelope analysis. Here the time-varying input envelope is mapped, at each instant in time, into the output envelope value at the same time using the static X-parameters. The results are valid (indicative of the actual device response) provided only that the modulation is narrow-band relative to the carrier. ADS 2009 Update 1 now allows for an arbitrary number of tones and arbitrary number of ports as well as built-in native support for X-parameter simulation.
Prior to this availability there was no direct way to investigate multiple tones around the main drive tone. FDD models are also inherently steady state models, naturally supporting the discrete harmonic tones used in single-tone harmonic balance, and not general or arbitrary waveforms. This limitation can be circumvented by coupling the Harmonic Balance solver with either circuit envelope or complex envelope solvers when more complex drive waveforms are needed for EVM and ACPR analyses. Both methods, Complex Envelope and Circuit Envelope, make use of the AM-AM and AM-PM information in the model and both assume that spectral widening is such that inter-modulation effects are narrow band centered about the carrier.
With the upcoming two-tone X-parameter capability added to Agilentís NVNA, the calibrated nonlinear cross-frequency vector distortion information can be used for designing distortion cancellation circuits and apply other design principles, such as derivative superposition,9 that previously could be applied only if there was confidence in accurate nonlinear device models. Extending the NVNA to measure three-port devices, such as mixers and converters, is also underway.
At IMS last year, Verspecht, Horns, Betts, Gunyan, Pollard, Gillease and Root reported an extension of the X-parameter model to include dynamics identified from multi-envelope X-parameter measurements on an NVNA with a pulsed stimulus with variable on/off ratios. The model was shown to correctly predict the transient RF response to time varying RF excitations including the asymmetry between off-to-on and on-to-off switched behavior as well as responses to conventional wide-bandwidth communication signals with the high peak-to-average ratios that excite long-term memory effects such as self-heating, dynamic bias effects and trapping phenomena. The approach was applied to an HBT transistor and a commercial PA module that exhibited significant memory effects and experimentally validated by two-tone NVNA measurements using novel envelope transient measurement techniques.14
Conclusion
Proprietary empirical models and extraction techniques for nonlinear devices are a costly and time-consuming effort for integrated device manufacturers. Lack of model availability represents a real bottleneck for designers while uncertainty over model quality is a leading cause of design failure. Recent breakthrough innovations in nonlinear characterization (i.e. measurement, modeling and simulation) look to compliment compact models with measurement-based black-box models similar in nature to S-parameters. For nonlinear devices, such models must accurately account for the amplitude/phase information of the DUTís spectral components, which will in turn depend on measurement parameters (i.e. stimuli, load impedances, etc.). Current commercial offerings are based on the Poly-harmonic Distortion model, which takes advantage of the harmonic superposition principle. Such models are derived using a new generation of measurement systems known as large-signal network analyzers or nonlinear vector network analyzer. Model accuracy is assured provided the simulation conditions reflect those of the measurement. Both model and measurement technology are evolving as the industry is adopting this new approach. While less general than a compact model, these measurement- based models and measurement systems are poised to bring relief to what had been a persistent bottleneck in the design process. n
Acknowledgment
The author gratefully acknowledges the support and contributions of the following individuals: D. Root, L. Betts, C. Plott, J. Civello and J. Smith (Agilent Technologies); S. Reyes and K. Van Diepen (Anritsu); M. Vanden Bossche (NMDG); M. Roth, T. Bednorz, J. Fries and J. Wolf (Rohde & Schwarz); and S. Hess and M. Edwards (AWR). Also, a very special thanks to Jan Verspecht for his impressive contributions to nonlinear device characterization and whose timely and detailed responses to my questions made this article possible.
X-Parameter is a registered trademark of Agilent Technologies Inc.
References
- http://users.skynet.be/Marc.Vanden_Bossche/nmdgvaria/LSNATechnologyTheory.pdf.
- J. Verspecht, ìCalibration of a Measurement System for High Frequency Nonlinear Devices,î Doctoral Dissertation, Vrije Universiteit Brussel, Belgium, November 1995.
- http://www.janverspecht.com/HTML/profile.htm.
- J. Verspecht and D. Root, ìPoly-harmonic Distortion Modeling,î IEEE Microwave Magazine, Vol. 7, No. 3, June 2006, pp. 44-57.
- http://www.home.agilent.com/agilent/redirector.jspx?ckey=1483944&action=ref&lc=eng&cc=US&cname=AGILENT_EDITORIAL.
- P. Blockley, D. Gunyan and J.B. Scott, ìMixer-based, Vector-corrected, Vector Signal/Network Analyzer Offering 300 kHz to 20 GHz Bandwidth and Traceable Phase Response,î 2005 IEEE MTT-S International Microwave Symposium Digest, June 12-17, 2005.
- U. Lott, ìMeasurement of Magnitude and Phase of Harmonics Generated in Nonlinear Microwave Two-ports,î IEEE Transactions, Vol. 37, No.10, October 1989, pp.1506-1511.
- A. Barel, ìHistory of Nonlinear Microwave Measurements,î Vrije Universiteit Brussel (Dept. ELEC); Pleinlaan 2; B-1050 Brussels, Belgium.
- M. Sipil‰, K. Lethinen and V. Porra. ìHigh-frequency Periodic Time-domain Waveform Measurement System,î IEEE Transactions, Vol. 36, No 10, October 1988, pp. 1397-1405.
- G. Kompa and F. Van Raay, ìError-corrected Large-signal Waveform Measurement System Combining Network Analyser and Sampling Oscilloscope Capabilities,î IEEE Transactions, Vol. 38, No. 4, April 1990, pp. 358-365.
- D. Williams, P. Hale and K.A. Remley, ìThe Sampling Oscilloscope as a Microwave Instrument,î IEEE Microwave Magazine, Vol. 8, No. 4, August 2007, pp. 59-68.
- M. Demmler, P.J. Tasker and M. Schlechtweg, ìOn-wafer Large-signal Power, S-Parameter and Waveform Measurement System,î Conference Record of INMMCí94-3rd International Workshop on Integrated Nonlinear Microwave and Milimeter-wave Circuits, Duisburg, Germany, October 1994, pp. 153-158.
- L. Betts, ìVector and Harmonic Amplitude/Phase Corrected Multi-envelope Stimulus Response Measurements of Nonlinear Devices,î 2008 IEEE MTT-S Microwave Symposium Digest, June 2008.
- J. Verspecht, J. Horn, L. Betts, D. Gunyan, R. Pollard, C. Gillease and D.E. Root, ìExtension of X-Parameters to Include Long-term Dynamic Memory Effects,î 2009 IEEE MTT-S International Microwave Symposium Digest, 2009, pp. 741-744.
