The planar inverted-F antenna (PIFA) is widely used in cellular phones, primarily due to its compactness and size.1 The demand for communication devices for personal communication systems has led to a constant search for ways to reduce the cellular phone dimensions. Applications, such as loudspeakers, cameras, etc., are emerging, and thus the complexity and the requirements of the antenna system continue to increase. It is expected that the volume available for the antenna will decrease, since the overall size of the mobile phone continues to decrease. However, antenna size reduction is obtained at the expense of antenna gain and bandwidth.2 This follows from the fact that an antenna is used to transform a bounded wave into a radiating wave.3 An antenna performs this transformation with poor efficiency when it is much smaller than a wavelength.4 The loss in antenna gain can be compensated to some extent by amplification. This is obviously not the case for the bandwidth. If the impedance match is much better than required, broad banding techniques could be used.5 For a given configuration, the design of the antenna should use the total volume available.6,7 The upper theoretical limit is never reached, and the design of small antennas is thus a trade-off between bandwidth and gain for the antenna chosen for the given application.2,8 Many authors have dealt with the issues regarding the minimization of antennas suitable for cellular applications. Skrivervik, et al. are the authors of the most recent publication.9
Another challenging task in minimizing the antenna is that the distance between the antenna and the other components, such as the loudspeaker and the camera, decreases as well. This motivates the need for information regarding how the antenna should be placed on the ground plane as well as the placement of other components with respect to the antenna and the ground plane. This task is also motivated by the fact that applications such as Bluetooth, diversity and multi-input-multi-output (MIMO) may require an extra antenna inside the mobile phone. Hence, information is needed regarding how these antennas could be oriented in order to minimize the coupling.10 Another important factor that also motivates the investigation of the near-field from cellular phones is the specific absorption rate (SAR), which is a measure of the energy absorbed by human tissue.
One way to obtain this kind of information is through the use of planar near-field measurements.11–14 The near-field is usually transformed to the far-field data; nevertheless, it is the raw, unprocessed, near-field data that is presented and used in this article. The purpose of this research is to determine whether the raw, unprocessed, near-field data can be used as a design parameter.
The main objective of this research is to investigate how the near-field is distributed at small distances from the ground plane of the PIFA antenna. The results show that, at distances very close to the antenna structure, it is the antenna element that dominates the field. At larger distances, however, the dominant radiated field is due to the current that is induced in the ground plane and not the current on the antenna element itself. This information could be used when one has to place two or more antennas within the same phone. The result could also be used to explain, and thus indicate, how to minimize the mutual coupling between the antenna elements. The location of the peak value of the electric field is discussed. The three principal electric field components are simulated in order to illustrate how the individual components contribute to the total field. The measured results are compared to the simulated results and discussed in terms of the radiation from the antenna element itself and from the ground plane of the antenna.
In order to analyse the antenna, the IE3D computer program16 was used to predict the performance of the antennas in terms of their scattering parameters and their input impedance as well as the electric field distribution at short distances from the antennas. The simulated results are compared with the corresponding experimental results to show the effectiveness of this approach. The measured results are in good agreement with theory.
Materials and Methods
The antenna configuration presented consists of two PIFAs with small differences in length and width. They are located on a 40 by 100 mm ground plane. The antenna A1 is 36 mm long, 1.2 mm wide and 7.5 mm high. The feed point is located 3.3 mm from the edge where a 90° bend forms the short to the ground plane. Antenna A2 is oriented parallel to A1 and is 35 mm long, 0.9 mm wide, 7.5 mm high, and the feed point is located 1 mm from the shorting pin. The separation between the PIFAs is 2.5 mm. The layout is illustrated in Figure 1.
Fig. 1 Antenna model and orientation.
A planar scanner is used to perform the measurements. The step size is 4 mm, leading to a total of 544 measurement points for a 64 by 124 mm area. This area covers the ground plane plus an additional 12 mm on each side of the ground plane.11 The probe used for these measurements is a three-dimensional E-field probe, designed for electric near-field component measurements up to 3 GHz.15 The measurements are carried out at 1950 MHz, that is at the resonant frequency of antenna A2. The measurement facility gives the total amplitude of the electric field as well as the x, y and z components. These measurements are compared to the results obtained from the IE3D computer program.
In the planar scanning technique, the probe is moved in a plane situated in front of the antenna and the received signal (amplitude) is recorded. The position of the probe is characterised by the coordinates (x, y, z0) in the xyz coordinate system of the antenna. During the scanning, z0 is kept constant, while x and y are varied. The field is measured at two distances: z0 = 2.5 and 22.5 mm, corresponding to free space distances of 0.016 l and 0.15 l, which are equivalent to an electric length of 6° and 52°, respectively. It should be noted that the distance between the ground plane and the measurement planes are 10 and 30 mm, since the antenna height is 7.5 mm.
Results and Discussion
The simulated and measured field distributions, shown in Figure 2, give the electric field amplitude at 2.5 mm above the radiating element. In all sub-figures, the highest field intensity (red) is found in the region where the PIFA elements are located, that is in the lower part of the figures.

Fig. 2 Simulated (a) and measured (b) electric field, 2.5 mm above the radiating element at 1950 MHz.
The shape of the total electric field corresponds to the shape of the antenna elements. It is seen that the largest contribution is located at the open end of the radiating elements. Due to the very narrow elements in the y direction, the field contribution from the x component is expected to be low, as indicated by one major contribution. The peak radiation of the x component is found at the open end of the radiating element. The difference observed when comparing the measured and the simulated x components could be caused by at least two things. First, the prototype is handmade, using a scalpel, and thus not perfectly rectangular, as in the simulation model. Secondly, if the prototype is not fully aligned, then the measured x component contains a y component as well. The y component follows the shape of the elements, that is two major contributions, both two long and narrow regions, as expected due to the shape of the antenna elements. For the z component, one can observe two long and narrow regions due to the shape of the antenna. The highest field amplitude is obtained above the antenna element itself. In both the simulated and measured cases, one could also observe a contribution from the z component that originates from the open end of the radiating element towards the centre of the ground plane.
Although the higher resolution for the simulated results yields better visualization of the trends, the measured results show good agreement. One of the most obvious differences, when looking at the total field and the x component of the electric field plot at 2.5 and 22.5 mm (see Figure 3) above the ground plane, is the different location of the maximum in the field intensity. In the lower plane (2.5 mm), the field seems to originate from the open end of the radiating element, that is the PIFA elements themselves. This fact changes when looking at the electric field obtained 20 mm further away. Here, it is more likely that parts of the radiated field originate from the geometrical centre of the element. The maximum of the z component is, at both distances, located above the feed and short pin. However, observing in the 2.5 mm plane, the major part of the z component contribution originates from the open end of the radiating element, whereas a null is observed in the 22.5 mm plane. The maximum of the y component is located at (x, y) = (30, 20). This is not above the radiating element, which indicates that some kind of radiation from the ground plane exists.
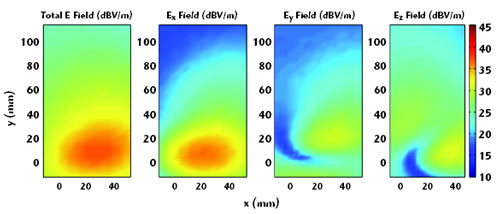
Fig. 3 Measured electric field components 22.5 mm above the radiating element at 1950 MHz.
Optimization of the Location of a Metallic Cube Having a Size of 7 ¥ 7 × 7 mm3
The size of the cube is assumed to model a loudspeaker or a camera. The simulated electric field component, 2.5 mm above the antenna ground plane at 1950 MHz (see Figure 4), can be compared with the corresponding simulations where the metallic cube is located at different locations. The location is varied from (x, y) = (0, 7) to (27, 7) in five steps, namely at x = 0, 6, 10, 20 and 27 mm from the left edge of the ground plane.
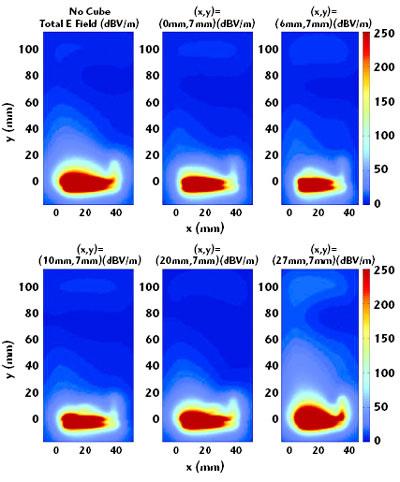
Fig. 4 Simulated total E field, 2.5 mm above the antenna, with a metallic cube located at different positions (F = 1950 MHz).
By comparing the shape of the total electric field, it can be seen that locating the metallic cube at either (x, y) = (20, 7) or (27, 7) affects the near-field the least. Most affected is the (x, y) = (0, 7) case. Here, the metallic cube is located nearest the open end of the PIFA arms. Using the raw data of the electric near-field to visualize the results gives rise to a rather subjective evaluation. In Figures 5, 6 and 7, the simulated reflection coefficients of antennas A1 and A2 and the mutual coupling are shown and can be compared in a more objective manner.

Fig. 5 Simulated reflection coefficient for antenna A1 for different locations of the metallic cube.

Fig. 6 Simulated reflection coefficient for antenna A2 for different locations of the metallic cube.

Fig. 7 Simulated mutual coupling for different locations of the metallic cube.
Changing the cube location from 0 to 27 mm, the resonant frequency of antenna A1 decreases from 1920 to 1905 MHz. The original resonant frequency of antenna A1 is 1910 MHz. For cube locations of (x, y) = (0, 7), (6, 7) and (10, 7) the bandwidth is increased significantly as compared to the original case. The wider bandwidth is caused by constructive interference between the metallic cube and the antenna arms.
When locating the metallic cube nearest to the shorting pin of the PIFA, that is at (x, y) = (27, 7), the resonant frequency is 1945 MHz. This is slightly higher than the resonant frequency of antenna A2 in the original case (1940 MHz). A decrease in resonant frequency to 1920 MHz is observed when the metallic cube is moved towards (x, y) = (0, 7).
From the reflection coefficient results shown, it is observed that the resonant frequencies of the two antennas change in opposite directions. When changing the location of the metallic cube from (x, y) = (0, 7) to (27, 7), the resonant frequency of antenna A1 is decreased from 1920 to 1905 MHz. Simultaneously, the resonant frequency of antenna A2 is increased from 1905 to 1945 MHz. This result explains the behaviour of the mutual coupling that is shown. The original case yields a mutual coupling of S21 = –3 dB. The strongest coupling of –1.6 dB is obtained at 1905 MHz, with the metallic cube located at (x, y) = (0, 7). This is a 3.4 dB stronger coupling as compared to the –5 dB obtained at (x, y) = (27, 7) case.
Conclusion
This study shows that metallic objects that are placed in the regions above the ground plane where the field intensity is the lowest, affect the antenna performance the least. Hence, the optimal location of a metallic object, which might be a loudspeaker or a camera, can be determined directly from the raw, unprocessed, electric near-field distribution.
In the cases where the metallic object is located closest to the open end of the radiating element, the antenna performance is affected the most. Thus, the conclusion is that metallic objects should be located in areas having a local minima in the electric field amplitude of the total field, and one should maximize the distance between the metallic object and the open end of the radiating elements.
References
1. K. Hirasawa and M. Haneishi, Analysis, Design, and Measurement of Small and Low Profile Antennas, Artech House Inc., Norwood, MA, 1991.
2. R.F. Harrington, “Effect of Antenna Size on Gain, Bandwidth and Efficiency,” Journal of Research of the National Bureau of Standards, D – Radio Propagation, Vol. 64D, 1960, pp. 1–12.
3. “The IEEE Standard Definitions of Terms for Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 17, 1969.
4. R.C. Hansen, “Fundamental Limitations in Antennas,” Proceedings of the IEEE, Vol. 69, February 1981.
5. R.E. Collin, “Minimum Q of Small Antennas,” Journal of Electromagnetic Waves and Applications, Vol. 12, 1998, pp. 1369–1393.
6. L.J. Chu, “Physical Limitations of Omni-directional Antennas,” Journal of Applied Physics, Vol. 19, 1948, pp. 1163–1175.
7. G.A. Thiele, P.L Detweiler and P.P. Penno, “On the Lower Bound of the Radiation Q for Electrically Small Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 51, No. 6, 2003, pp. 1263–1269.
8. H.A. Wheeler, “Fundamental Limitations of Small Antennas,” Proceedings of the IRE, Vol. 35, 1947, pp. 1163–1175.
9. A.K. Skrivervik, J.F. Zürcher, O. Staub and J.R. Mosig, “PCS Antenna Design: The Challenge of Miniaturization,” IEEE Transactions on Antennas and Propagation, Vol. 43, No. 1, January 2001, pp. 12–27.
10. J. Thaysen, “Mutual Coupling Between Two Identical Planar Inverted-F Antennas,” IEEE Antennas and Propagation International Symposium and USNC/URSI National Radio Science Meeting Digest, 2002, pp. 504–507.
11. J. Appel-Hansen, “Antenna Measurements,” Ch. 8 in The Handbook of Antenna Design, A.W. Rudge (Ed.), Peter Pelegrinus Ltd., 1982.
12. R.C. Baird, A.C. Newell and C.F. Stubenrauch, “A Brief History of Near-field Measurements of Antennas at the National Bureau of Standards,” IEEE Transactions on Antennas and Propagation, Vol. 36, No. 6, June 1988.
13. J. Thaysen and K.B. Jakobsen, “Near-field Distribution from a Planar Inverted-F Antenna,” Proceedings of the Twelfth International Conference on Antennas & Propagation, University of Exeter, UK, 2003, p. 4.
14. Y. Gau and I. Wolff, “Miniature Electric Near-field Probe for Measuring 3-D Fields in Planar Microwave Circuits,” IEEE Transactions on Microwave Theory and Techniques, Vol. 46, No. 7, July 1998, pp. 907–913.
15. Data sheet, “3-dimensional E-field Probe for Small Band Applications,” 2002, www.speag.com.
16. “IE3D User’s Manual, Release 8,” Zeland Software Inc., Fremont, CA, 2001.
Jesper Thaysen received his MSc degree from the Technical University of Denmark, Kgs. Lyngby, Denmark, in 2000. He is currently working toward his PhD degree. Since 2001, he has been with Nokia Denmark. His current fields of interest include broadband antennas, small antennas and multi-element antennas. He can be reached via e-mail at jesper.thaysen@nokia.com.
Kaj B. Jakobsen received his MScEE degree from the Technical University of Denmark, Kgs. Lyngby, in 1986, his PhD degree from the University of Dayton, OH, in 1989, and his graduate diploma in business administration, organization and management from Copenhagen Business School, Denmark, in 2000. Since 1990, he has been a professor at the Technical University of Denmark, where he was named “Teacher of the Year” in 1994. His research interests include GPR, antennas, microwaves, electromagnetics and related interdisciplinary topics. He can be reached via e-mail at kbj@oersted.dtu.dk.
