1. Introduction
The microstrip resonator has been widely used to measure the dispersion, phase velocity, and effective dielectric constant in microstrip structures cause Because of its high Q-factor and structural simplicity, it also finds broad applications in microwave and millimeter-wave circuits such as filters; duplexers, oscillators, mixers, couplers, and antennas [1].
Printed bandpass filters are widely used elements in various microwave subsystems due to their repeatability, reliability and low price. Practically, their only “cost” is the occupied area on a printed board. Because of that many recent papers discuss various printed filter configurations having size reduction as one of the most important design goals [2].A bandpass filter using microstrip ring resonators with 25% size reduction compared to the conventional microstrip filter with coupled halfwavelength resonators was proposed in [1]. The papers [3-6] analyses various types of resonators filter design. Most of these filters have wider stopbands that contain deep zeros in proximity to the passband region. The most efficient way in order to obtain a filter with maximum size reduction is by using the microstrip technique in which each filter’s lumped component is realized as microstrip transmission line. Further optimization and tuning of the microstrip circuit would produce an equivalent microstrip circuit with certain percentage of size reduction relatively compared to the parallelcoupled filters. The center frequency is designed to be at 2.5GHz, which describes the operation of the filter with a maximum gain.
2. Concept
Figure 1

Figure 1 Basic Electric Scheme of proposed filter
shows a basic electric scheme of the proposed filter that consists of four identical resonators (Q1–Q4) electrically coupled by capacitors Cr [2].
Table 1

Table 1 Values of corresponding lumped components in Figure 1
shows the values of corresponding lumped components in Figure 1.Although the scheme has only four variables, Cp, Cr, L1, and L2, by varying their values it is possible to obtain filters with different bandwidths. The overall filter is square-shaped in order to minimise the space occupied [2]. The inductance L1 and L2 behaves as narrow microstrip transmission lines. For the loaded (input and output) resonators those microstrip transmission lines are divided into two unequal parts by input and output 50 Ω microstrip lines in order to achieve the 00 feed structure [6]. The microstrip line within the resonator is altered for minimisation of the resonator and overall filter size, and terminated on both ends with wide microstrip patches that form required capacitances to ground (Cp). The coupling capacitances Cr are formed between adjacent pairs of patches belonging to the neighbouring resonators [2].
3. Design and Results
Figure 2
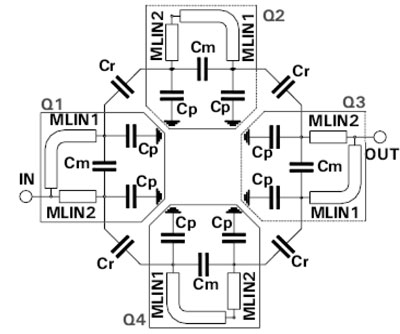
Figure 2 Circuit Simulator Scheme
The scheme from Figure 2 was used in a circuit simulator for the optimisation of the filter layout, mainly to optimise the width and the lengths of the microstrip transmission lines and to estimate the influence of the capacitance Cm, which tends to lower the filter’s centre frequency and to broaden the passband, as well as to take into account the components’ losses [2]. The lengths and widths of each microstrip transmission line are tuned and optimized in order to obtain center frequency at 2.5GHz and lower and upper 3dB cut-off frequencies at approximately 2.4GHz and 2.6GHz accordingly. Both capacitances and inductances are realized as microstrip transmission lines with impedance ZO =50ohm. The substrate used for simulation purposes and further implementation purposes is Rogers RO3010 (€ = 10.2 , h = 0.635mm). By using a higher € and thinner substrate, a smaller filter size could be achieved. Since the main goal or objective of the design is achieving a small filter size, the substrate RO3010 is suitable for optimum performance.
Figure 3

Figure 3 Photograph of the realised filter
shows a photograph of the realized filter. The filter is squared-shaped with dimension 8.5mm x 8.5mm (72mm 2 ) while filter from [2] occupies 27mm 2. The further center frequency increasing would lead to impractically small filter size. Because of that a filters layout at these frequencies has to be adjusted so that parasitic capacitance of transmission lines within the filters’ resonators are used to provide required ultra-small capacitances to ground (Cp). The design filter dimension is smaller compared to the conventional filter referenced in [3] that occupies 256 mm 2 . As a result the proposed filter has a significant size reduction of 72% compared to the conventional microstrip filter in [3]. This size makes it suitable for integration within various microwave subsystems.
Figure 4

Figure 4 Simulated and measured S11 and S21 parameters of the filter
shows simulated and measured S11 and S21 frequency response of the filter. The agreement between the measured results and the results from Advanced Design System (ADS) analysis is excellent. The realized filter has pass-band at central frequency of 2.45GHz, which differs from the designed value for less than 2%. This difference is caused by tolerances during filter’s fabrication. The biggest influence has the width of microstrip transmission lines within the filter’s resonators. The insertion loss at the central frequency is 2.4 dB. The measured 3dB bandwidth is 8.6%, while 1dB bandwidth is 6.5% with return loss in the same frequency range better than 15 dB. The attenuation in the lower stop-band is around - 54dB and around -62dB in the upper stop-band.
Conclusions
A new type of capacitive coupling of identical resonators to form a symmetrical microstrip bandpass filter is designed. The symmetrical approach tends to produce a more compact filter with less coupling effect in its realization. Its compact nature minimizes required space for realization and is suitable for integration within RF and microwave subsystems. The agreement between the measured and simulated results is excellent.
Acknowledgment
The author would like to thank Universiti Sains Malaysia (USM) for supporting this project.
References
1. Wu, Q.S., Xue, Q., and Chan, C.H.: ‘Bandpass filter using microstrip ring resonators’, Electron. Lett., 2003, 39, (1), pp. 62–64.
2. Jovanovic, S. and Nesic, A. Microstrip banpass filter with new type of capacitive coupled resonator, Electronic Letters, 41(1), 12-13.
3. Tsai, C.-M., Lee, S.-Y., and Lee, H.-M.: ‘Transmission-line filters with capacitively loaded coupled lines’, IEEE Trans. Microw. Theory Tech., 2003, 51, (15), pp. 1517–1524.
4. Kuo, J.-T., and Shih, E.: ‘Microstrip stepped impedance resonator bandpass filter with an extended optimal rejection bandwidth’, IEEE Trans. Microw. Theory Tech., 2003, 51, (15), pp. 1154–1159.
5. Lee, S.-Y., and Tsai, C.-M.: ‘New cross-coupled filter design using improved hairpin resonators’, IEEE Trans. Microw. Theory Tech., 2000, 48, (12), pp. 2482– 2490.
6. Tsai, C.-M., Lee, S.-Y., and Tsai, C.-C.: ‘Performance of a planar filter using a 0_ feed structure’, IEEE Trans. Microw. Theory Tech., 2002, 50, (10), pp. 2362– 2367
