The appeal of a low cost, high performance frequency synthesizer as a key component of virtually any test and measurement (T&M), communication and monitoring system is recognized throughout the microwave industry.1–5 Although all synthesizers exhibit significant differences as a result of specific applications, they share basic fundamental design objectives as listed below.
Basic Requirements
Frequency Coverage and Resolution
A single tone or relatively narrowband (10 to 20 percent) LO signal can be just enough for many applications. However, modern digital broadband systems require much wider frequency coverage extending to a few octaves. Wide bandwidth and fine frequency resolution (down to 1 Hz and below) are usually “musts” in test and measurement applications such as laboratory synthesizers, network and spectrum analyzers, and synthetic instruments. For synthesizer manufacturers, it may be advantageous to develop a broadband “generic” solution, which can cover a number of applications.
Output Power
Required output power levels can range over wide limits, depending on a particular application. A typical scenario assumes the frequency synthesizer as an LO source, driving a frequency mixer in a variety of up- and down-conversion schemes. This normally requires +10 to +17 dBm output signal, although some applications need even more power.
Spurious Content
Spurs are undesired artifact products created by synthesizer components at discrete frequencies. Spur location and level are determined by a particular synthesizer architecture and frequency plan. In microwave communication systems, the spurious products can limit the ability of the receiver to resolve and process a desired signal. Thus, the synthesizer spur level has to be minimized and should not usually exceed –60 dBc relative to the main signal, although many applications require bringing this level down to –80 dBc and below. This requires a specific design effort and is usually a tradeoff between other synthesizer parameters, such as phase noise, step size and tuning speed.
Phase Noise and Stability
Phase noise is one of the major parameters that ultimately limits the sensitivity of receiving systems. Synthesizer stability and close-in phase noise strictly depend on the reference signal as well as the particular synthesizer architecture used to derive its output from the reference. Indirect synthesizers also rely on tunable oscillator noise, which can supersede the multiplied reference noise at high frequency offsets. A good example is a YIG-tuned oscillator, typically exhibiting –120 to –130 dBc/Hz at 100 kHz offset from 2 to 10 GHz and above.
Tuning Speed
Tuning (switching) speed determines how fast the synthesizer jumps from one desired frequency to another. The time spent by the synthesizer jumping between frequencies becomes more and more valuable, since it cannot be used for data processing. New communication systems require higher frequency switching speeds to increase the effective data rate. Even traditionally low speed test and measurement applications would like faster tuning. For example, a new vector network analyzer based on four independent, very fast tuning speed frequency synthesizers has recently been introduced.6 The synthesizer developers have to consider this trend; target “throughput” numbers (that include all required internal calculations and digital control) should be in the microseconds range.
Power Consumption and Mechanical Constraints
Modern microwave equipment tends to be smaller, lighter, requiring lower voltage and consuming less power. Thus, new synthesizer designs should utilize high integration ICs, avoiding bulky and power hungry components, such as YIG oscillators and filters.
Particular Demands
The microwave industry feels persistent pressure to deliver higher performance, higher functionality, smaller size, lower power consumption and lower cost synthesizer designs. However, the major technology challenge is in increasing the synthesizer tuning speed as dictated by the ongoing increase of the data rates of modern microwave systems. While many T&M and communication systems still work adequately with millisecond switching speed, new equipment demands microsecond operation together with performance (phase noise, spurious) similar to the low speed designs. Obviously, this presents serious design difficulties and tradeoffs. Another challenge is cost reduction. Although it is considered to be a fairly “standard” requirement, it drastically narrows the designer’s choice. These particular requirements—microsecond tuning speed (together with YIG-based phase noise and spurious characteristics) and low cost—are likely to be the key drivers in the development of the new frequency synthesizers.
Architectures
While reviewing traditional frequency synthesizer technologies, the current technology trend toward increasing the synthesizer tuning speed is specifically addressed as well as reducing its complexity and cost. Various synthesizer architectures along with their main characteristics are described below.
Direct Analog Synthesizers

The main job of any synthesizer is translating one or more reference signals to a number of output frequencies with a required step size. Direct analog synthesizers are realized by mixing base frequencies followed by switched filters, as depicted in Figure 1. The base frequencies can be extracted from low frequency (crystal, SAW) or high frequency (DRO, sapphire, metal cavity, CRO, etc.) oscillators by frequency multiplication, division, or phase locking.7
The key advantage of a direct analog technique is its extremely fast switching speed, ranging from micro- to nanoseconds. Another distinct advantage is the ability to generate very low phase noise output, due to the use of components (such as mixers) with negligibly low residual noise, compared with the base frequency sources.

Thus, the direct analog synthesizer phase noise mainly depends on the noise of the available reference sources and can be fairly low. The main disadvantage of this topology is a limited frequency coverage and step size. In the example shown, only eighteen output frequencies can be generated, even by utilizing both mixer sidebands.
The number of output frequencies can be increased by using a higher number of base frequencies or/and mixer stages, as shown in Figure 2.
However, this rapidly increases the design complexity and overall component count. An effective solution is the use of a direct digital synthesizer module (DDS) to increase the minimum step size required from the direct analog portion, as shown in Figure 3.

Another serious problem is the large amount of undesired mixing products, which have to be carefully planned and filtered out. Special attention should be paid to the switched filter isolation and leakage. Although a large variety of mixing and filtering organization schemes is possible, they tend to be hardware intensive if small frequency steps and wide coverage are required. Therefore, while this approach offers excellent tuning speed and phase noise characteristics, its usage is limited to applications where fairly high cost can be tolerated.
Direct Digital Synthesizers
In contrast to traditional concepts, the direct digital synthesizers (DDS) utilize digital processing to construct an output signal waveform from a base (clock) frequency,8 as shown in Figure 4.
Initially, a digital representation of a desired signal is created and then it is reconstructed with a digital-to-analog converter (DAC) to a sinusoidal or any other desired signal shape.
This process is extremely fast, mainly limited by the digital control. This results in very high switching speeds, comparable with direct analog schemes. DDS also provides reasonably low phase noise even showing an improvement (limited by its residual noise floor) over the phase noise of the clock source itself. From this point of view, DDS acts as a frequency divider. However, the most valuable DDS feature is its exceptionally fine frequency resolution, which is determined by the length of the DDS phase accumulator; sub-hertz levels are easily achieved.
The main disadvantages are limited usable bandwidth and spurious performance. While a DDS starts working from nearly DC, its highest frequency is limited by the Nyquist criteria to within one half of the clock frequency. Moreover, a practical design requires an output low pass filter for reconstructing the signal waveform, which further decreases the highest operation frequency to approximately 40 percent of the clock signal. Another serious problem is the high spurious content due to quantization and DAC conversion errors.
From a spurious point of view, a DDS can be thought of as a mixer. While the spur location can be easily calculated, its amplitude is much less predictable. As a general rule, lower order spurs are the strongest (although fairly high order spurs must be taken into account during DDS frequency planning).
The spur amplitude normally increases with a clock frequency increase, which places another limitation on the DDS usable bandwidth. Practical solutions usually range from a few tens to a few hundreds of megahertz output with a broadband spur-free dynamic range (SFDR) level of –50 to –60 dBc. Direct multiplication of the DDS output is obviously prohibited due to further spur degradation.
A number of solutions (both hardware and software based) can be used to reduce the DDS spurs.9 Hardware techniques are usually based on up-conversion of the DDS signal followed by a frequency divider, as shown in Figure 5.
It effectively reduces the DDS spurious content at a 20 dB/decade rate, inherent to the frequency division process.
Unfortunately, it also reduces the output bandwidth, requiring more LO frequencies and filters, resulting in a higher component count similar to the direct analog schemes, as shown in Figure 6.

On the other hand, software techniques involve effective frequency planning and spur separation. These techniques are based on the fact that a DDS spur location is a function of its output and clock frequencies (similar to the frequency mixers).
Therefore, for a given output frequency, one can move (and then filter out) an undesired spur by changing the DDS input clock frequency and tuning command. This technique can be effectively combined with PLL architectures, which provide a variable clock source as well as effective PLL-based output filtering.
This software technique works fairly well for relatively low order spurious products. The spur density normally increases proportionally to the spur order, which limits the practical usage of this technique to –70 to –80 dBc levels. Due to the mentioned bandwidth and spur limitations, the DDS technique alone is rarely utilized at microwave frequencies. Rather, DDS is used as a fine frequency resolution module in direct analog and indirect architectures.
Indirect Frequency Synthesizers
Indirect frequency synthesizers utilize phase locking (PLL) techniques offering smaller size and lower complexity, compared to direct analog schemes.10–14 A typical single-loop PLL synthesizer includes a tunable voltage-controlled oscillator (VCO), the output of which is fed back to a phase detector (PD) via a power splitter (PS) and a frequency divider with a variable frequency division ratio N, as shown in Figure 7.
The other input of the phase detector is a reference signal equal to a desirable frequency resolution. The phase detector compares the signals at both inputs and generates an error voltage which, following filtering and amplification (optionally), slews the frequency of the VCO to the lock frequency given by f = FREF x N, where FREF is the reference frequency at the phase detector input.
The major advantages of this scheme are reduced levels of spurious signals, owing to the low pass filter action of the loop, and a much lower level of complexity compared with the direct analog synthesizers. The main disadvantages are longer frequency switching time (which is inversely proportional to the loop bandwidth and consequently step size) and considerably higher phase noise in comparison with direct analog techniques.
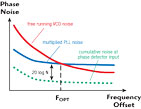
The single-loop synthesizer phase noise performance within its loop filter bandwidth is given by λ = λPD + 20 logN, where λPD is the cumulative phase noise of the reference signal, phase detector, feedback divider, loop filter and amplifier referred to the phase detector input, as shown in Figure 8.
Thus, the phase noise is affected by the large division ratios required to provide a high frequency output with a fine resolution. For example, in order to get 10 GHz output with 1 MHz step size, the feedback divider ratio has to be 10000, which corresponds to an 80 dB phase noise degradation. Moreover, programmable dividers are usually not available at high frequencies, thus an additional fixed divider (prescaler) is required.
In this case, the total division ratio will increase by the prescaler division coefficient resulting in further phase noise degradation. Obviously, this simple scheme does not allow utilizing the noise performance of modern low noise reference oscillators. Moreover, the discrete spurs at multiples of the reference frequency tend to be proportional to the loop division ratio N, which also leads to spurious degradation.10 As a result, the single-loop schemes are only used in moderate performance applications.

The synthesizer’s main characteristics can be drastically improved by employing a frequency conversion (mixing) within the synthesizer feedback path, as shown in Figure 9. Here, the VCO output frequency is converted with the aid of an offset frequency source in order to minimize the maximum frequency division ratio and the number of ratios that otherwise would be necessary.10 The offset signal can be produced from the same reference using additional PLLs (multi-loop schemes) or frequency multipliers.
An attractive solution is a sampling (harmonic) mixer that utilizes multiple harmonics created by a built-in step recovery diode. This approach usually leads to a shorter bill of materials in comparison with fundamental mixing schemes. The main drawback of the sampling mixer is its sensitivity to circuit parameters; making one work properly is not trivial.
Depending on particular phase noise and step size requirements, a higher number of mixing stages can be needed which leads to a higher level of complexity.
Another problem associated with any frequency-mixing scheme is a possible false lock to undesired (that is a wrong sideband) mixing products. This type of failure requires a sufficiently accurate coarse-tuning mechanism. A DAC may be included to coarse-tune the VCO to approximately the correct frequency.
This acquisition aid requires linear (and repeatable) VCO tuning characteristics over the operating temperature range as well as precise frequency calibration to compensate the VCO temperature drift. Moreover, DACs are usually too noisy, adversely affecting the synthesizer phase noise performance, if they are not properly removed after the initial frequency acquisition.10 Another way to reduce the overall loop division ratio is based on the use of a fractional divider.
Fractional division coefficients are achieved by dividing the input frequency by N+1 every M cycles and dividing by N the rest of the time.15 In this case, the average division coefficient will be (N+1)/M, where N and M are integers.

For a given step size, fractional-N schemes allow a higher phase detector comparison frequency that potentially results in better phase noise and tuning speed characteristics. The main disadvantage of the fractional-N technique is excessive spurious levels, due to phase errors inherent to the fractional division mechanism.
A very effective solution is the use of a DDS module, which is essentially a fractional divider as well. The DDS can be inserted into the reference or divider path, as shown in Figures 10 and 11, respectively.
Special attention should be paid to the DDS spurious signals, which are degraded by the loop division ratio at the same 20 dB/decade rate.

From this point of view, the configuration using the DDS in the reference path is more flexible, since it allows minimizing or completely removing the loop division by inserting an additional offset signal as previously discussed.
Although no divider is shown when the DDS is inserted in the divider path, this configuration also brings spurious degradation, set by the ratio of the DDS input (clock) and output frequencies.
The DDS spurious reduction techniques previously described can be effectively utilized here, enjoying natural, high rejection PLL filtering. Although these solutions complicate the overall design, the complexity can be effectively spread and optimized, which leads to a high performance and reasonably priced design.
VCO Choice
Any indirect synthesizer design strongly depends on the VCO characteristics. Historically, synthesizer developers have relied on YIG-tuned oscillators featuring broadband operation and excellent phase noise performance.
The YIG oscillators also offer very linear (and repeatable) tuning characteristics that simplify the synthesizer coarse-tuning algorithm in multi-loop schemes. Beside this, the YIG oscillators feature relatively low and nearly constant tuning sensitivity that also helps to optimize the synthesizer spurious performance.
These unique features permitted the YIG-based microwave synthesizers to dominate during the last few decades. However, the high power consumption, large size, high cost and especially low speed inherent to the YIG oscillators have recently contributed to a shift to solid-state VCO architectures. Currently, high frequency (up to 10 GHz and above) VCOs are readily available as low cost, surface-mount IC components.
Since the VCO noise is considerably worse compared to its YIG counterpart, the designer should primarily rely on the reference source. Today’s commercial crystal oscillators offer noise performance of –160 to –176 dBc/Hz at 20 to 100 kHz offset for a 100 MHz output.16 These numbers are translated to –120 to –136 dBc/Hz at the same offset and for a 10 GHz output, which corresponds or even supersedes the performance of the best YIG oscillators.
Of course, it is assumed that this translation is not affected by the synthesizer system noise floor. Although this assumption calls for very advanced synthesizer solutions, the net effect is evident: the VCO-based designs can potentially achieve much faster tuning speed, together with comparable phase noise and spurious performance without the use of expensive, bulky and power hungry YIG devices.
Future Projections
The direct analog synthesizer is today’s most advanced technique, offering unprecedented speed and phase noise performance. Although its complexity is in conflict with the industry “standard” cost-reduction requirement, it can be an excellent choice for some applications where fairly high cost can be tolerated. Some cost reduction is expected with the development of higher frequency, lower spurious DDS ICs, which can simplify the direct analog synthesizer design. Direct digital synthesizers have a tremendous potential for future growth as a result of exceedingly rapid developments in GaAs, silicon and SiGe devices.
The extension of a DDS usable bandwidth (together with its spur content reduction) is the key improvement required by the industry. It will directly impact the performance of direct analog and indirect architectures where a low cost DDS IC becomes a “must have” building block. However, the most exciting near-term developments are likely to be associated with the VCO-based indirect technologies.
Much of the progress here will be brought by reduction of the system residual noise floor, in order to extend the PLL bandwidth to much higher frequencies. The most dramatic change will occur when the optimum loop bandwidth extends to a few megahertz, where solid-state VCO noise becomes competitive with the YIG devices.
Equipping the synthesizer with a low noise reference gets a “YIG-grade” noise performance, but offers an amazingly faster, microsecond-range tuning speed. These characteristics, accompanied with the low cost inherent to the indirect designs, are likely to secure their domination in the foreseeable future.
References
- J. Browne, “Frequency Synthesizers Tune Communications Systems,” Microwaves & RF, March 2006.
- V. Kroupa, Frequency Synthesis Theory, Design and Applications, John Wiley & Sons Inc., Hoboken, NJ, 1973.
- V. Manassewitsch, Frequency Synthesizers Theory and Design, Third Edition, John Wiley & Sons Inc., Hoboken, NJ, 1987.
- U. Rohde, Microwave and Wireless Synthesizers: Theory and Design, John Wiley & Sons Inc., Hoboken, NJ, 1997.
- J. Klapper and J. Frankle, Phased-locked and Frequency Feedback Systems, John Wiley & Sons Inc., Hoboken, NJ, 1972.
- Rohde & Schwartz, “A 24 GHz Network Analyzer,” Microwave Journal, Vol. 48, No. 10, October 2005, pp. 136–142.
- Z. Galani and R. Campbell, “An Overview of Frequency Synthesizers for Radars,” IEEE Transactions on Microwave Theory and Techniques, Vol. 39, No. 5, May 1991, pp. 782–790.
- V. Kroupa, Direct Digital Frequency Synthesizers, IEEE Press, Piscataway, NJ, 1999.
- T. Endres, R. Hall and A. Lopez, “Design and Analysis Methods of a DDS-based Synthesizer for Military Space Borne Applications,” 1994 IEEE International Frequency Control Symposium Proceedings, pp. 625–632.
- W. Egan, Frequency Synthesis by Phase Lock, John Wiley & Sons Inc., Hoboken, NJ, 2000.
- R. Best, Phase-locked Loops—Theory, Design and Applications, McGraw-Hill, New York, NY, 1984.
- U. Rohde, Digital PLL Synthesizers: Design and Applications, Prentice Hall, Upper Saddle River, NJ, 1983.
- A. Blanchard, Phase-locked Loops, John Wiley & Sons Inc., Hoboken, NJ, 1976.
- F. Gardner, Phaselock Techniques, Second Edition, John Wiley & Sons Inc., Hoboken, NJ, 1979.
- Fractional-N Synthesizer, Application Note, Synergy Microwave Corp., www.synergymwave.com.
- Valpey Fisher Corp., “A High Frequency Reference Module,” Microwave Journal, Vol. 48, No. 4, April 2005, pp. 142–144.

Alexander Chenakin received his PhD degree from Kiev Polytechnic Institute, Ukraine, and has worked in a variety of technical and managerial positions around the world. He is presently director of the frequency synthesis group at Phase Matrix Inc., where he leads the development of advanced frequency synthesizer products for test and measurement applications. His professional interests include microwave frequency generation components and subsystems.
