The fast fourier transform (FFT) approach to the method of moments (MoM) is well known for providing high accuracy, high dynamic range and robust electromagnetic (EM) analysis of planar circuits. The FFT consistently calculates the coupling between subsections to full numerical precision; no error is introduced by complex multi-dimensional numerical integration.

However, use of the FFT does have a trade-off. When the FFT is used for digital signal processing, the time signal being processed must first be uniformly sampled in the time domain. FFT-based EM analysis is exactly analogous in that the surface of the planar circuit must be uniformly sampled in the space domain. The small FFT cells are then merged together to form large rectangular subsections. While the merging must be performed intelligently, the large rectangular subsections provide speed, and the FFT provides accuracy, especially for "Manhattan" circuits, or circuits with mostly rectangular outlines.
Non-Manhattan circuits can still be done; however, they tend to require a lot of small subsections, as shown in Figure 1 . This slows the analysis but maintains full accuracy. An alternative for quickly analyzing non-Manhattan circuits is to use arbitrary size and orientation rectangular and triangular subsections, as shown in Figure 2 . Such subsections can be placed closer to the edges of arbitrary metal. The problem now is that multi-dimensional numerical integration must be used, and the resulting reduction in accuracy and dynamic range must be tolerated. In addition, huge numbers of small triangles and rectangles are still required for smooth curves.
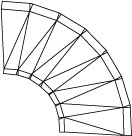
Follow The Curve
The solution is to retain the fine, underlying FFT mesh, and then merge the FFT cells into large subsections that follow curving transmission lines. While conceptually simple, there are actually a lot of hidden difficulties. In fact, the development of conformal meshing required a full decade of intense research to completely solve this deceptively simple looking problem.1,2
One of the hidden difficulties is that current naturally flows strongest on the edge of any planar conductor. This is called the edge effect. The edge effect must be included for an accurate analysis. Normally, the edge effect is included by using narrow subsections along conductor edges. However, the number of subsections quickly becomes too large for curving edges, even if arbitrary rectangles and triangles are used.
Conformal meshing solves this problem by automatically assigning more current to cells at the edge. Now a few large subsections can be used to follow curving transmission lines rather than the previously required multitudes of tiny rectangles and triangles, and high accuracy is maintained because the edge effect is still included.

Current Switching Sides
Figure 3 shows a spiral inductor on silicon3 (vertical axis expanded). It uses a two-layer model for the thick conductors.4 Figure 4 shows the measured versus calculated S-parameters, using an independently determined dielectric layer stack-up exactly as provided by Motorola. No attempt was made to tune the geometry. Analysis time on a 3 GHz class P4 computer is 5 min 48 sec per frequency with analysis at only six frequencies needed to provide a complete spectrally rich data set from 0.1 to 10 GHz. The conformal subsections are all about one-half spiral turn long.
Without conformal mesh, analysis of this spiral, including edge effect and thickness, requires one week or more for even the fastest of EM tools. Conformal mesh is an enabling technology.
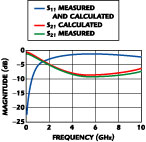
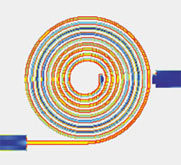
Figure 5 shows the current distribution on the bottom side of the spiral's thick metal. Especially intriguing is the edge effect current. Notice that it starts out with high (red) current on both edges of the spiral line. Following the spiral, the current switches sides every several turns. Edge effect current flowing on only one side of a line nearly doubles metal loss. To increase inductor Q, one can consider splitting the line into two narrow lines periodically. Then the two lines can swap sides periodically (using air bridges), forcing edge effect current to remain evenly split. Such alternatives can be quickly evaluated using conformal mesh.
Figure 6 shows the same inductor (vertical axis extremely expanded) analyzed with a much smaller cell size. Each cell in Figure 5 has now been converted into 16 exceptionally tiny cells. The S-parameters are almost exactly the same, so this analysis actually represents a grievous waste of numerical resources; however, it does illustrate the immense power of conformal meshing. Being able to analyze the spiral meshed as finely as this means 16 spirals meshed as in Figure 5 can be simultaneously analyzed all in one single (lengthy) analysis. The spiral of Figure 6 consists of 1.7 million conformal mesh cells, perhaps the largest circuit ever analyzed by a non-iterative MoM EM analysis.
Conformal mesh is being introduced in Sonnet's Version 9, to be available Q3 2003. The new release also includes other enhancements not described here, such as automated generation of thick metal, automatic documentation generation, equations, and interface to AWR's Microwave Office. Conformal mesh works especially well in combination with Sonnet's industry-leading Adaptive Band Synthesis (ABS) interpolation.
Conformal mesh, by generating large subsections which follow smoothly curving lines and including the edge effect, now allows the accuracy and speed of FFT-based EM analysis to be realized for curving non-Manhattan circuits. This marks a huge increase in the range of circuits that can be accurately analyzed, an appropriate culmination of 10 years of intense research.
Sonnet® is a registered trademark of Sonnet Software Inc.
References
1. J.C. Rautio, "A Conformal Mesh For Efficient Planar Electromagnetic Analysis," IEEE Transactions on Microwave Theory and Techniques , accepted for publication January 2004.
2. US Patent No. 6,163,762, December 19, 2000.
3. Data courtesy of Motorola, uses Motorola's High Voltage IC (HVIC) Si RF-LDMOS process on 90 micron thick, high-conductivity silicon.
4. J.C. Rautio and V. Demir, "Microstrip Conductor Loss Models for Electromagnetic Analysis," IEEE Transactions on Microwave Theory and Techniques , Vol. 51, No. 3, March 2003, p. 921.
Sonnet Software Inc., North Syracuse, NY (315) 453-3096, www.sonnetsoftware.com. Circle No. 300

