This article is intended to provide insight into the effective operation of variable gain amplifiers (VGA) in automatic gain control (AGC) applications. Figure 1 is a general block diagram for an AGC loop. The input signal passes through the VGA to produce the output level to be stabilized. The detector's output is compared against a setpoint voltage to produce an error signal, which is then integrated to produce a gain control voltage. This is applied to the control input of the VGA. The attenuator shown between the VGA and the detector is used to align the maximum output level of the VGA with the maximum input level of the detector.

In the course of this article several key issues will be addressed, including VGA types, loop dynamics, detector types, the operating level of VGA and the operating level of the detector. Then an example application revolving around an AD8367 VGA will be presented for further discussion of the material.

VGA Types

There are two major classes of VGA in use today. The first is the so-called IVGA (input VGA), which can be regarded as a passive variable attenuator followed by a fixed-gain amplifier. The second type is the output VGA (OVGA), which is essentially equivalent to a fixed-gain amplifier followed by a passive attenuator.

An IVGA is the preferred choice for a receive AGC system because the available output level at low distortion is relatively independent of the gain setting. This is the desired trait for an AGC system, whose very object is to maintain a constant output in the face of varying input signal amplitude.

The OVGA is generally ill suited to AGC applications because of its reduced output signal handling capability at low gain settings and therefore will not be discussed further here.

When a single IVGA is used in a situation in which the VGA sets the system noise floor, the output SNR is essentially independent of the input signal; it does not improve as is often preferred. Occasionally, it is desirable to cascade two VGAs in order to ameliorate this behavior or simply to obtain more gain control range. Doing so requires proper coordination of the gain control inputs of the two devices.

If the gain control of only the second stage VGA is manipulated in the weak signal regime, the signal level to the first stage VGA's amplifier increases with increasing input level, so the output SNR improves with increasing input level. It is necessary to hand off the gain control from the second stage to the first stage only when overload of the first stage's amplifier is imminent.

Alternatively, the two gain control inputs may simply be driven in parallel, in which case the output S/N (expressed in dB) improves at half the rate at which the input level (also expressed in dB) rises. In cases where the VGAs used have residual ripple in their gain control functions, an additional benefit of this approach can be obtained if the two gain control input signals are intentionally offset by half the period of the ripple. This can provide considerable reduction of the ripple.

One of the benefits of using an IVGA in an AGC loop is that the VGA's gain control voltage bears an accurate logarithmic relationship to the input signal level when the loop is in equilibrium. This means that the gain control voltage may also be used as an excellent received signal strength indicator (RSSI).

Loop Dynamics

Response time is an important issue when designing any AGC loop. There is usually a compromise between having the loop respond to undesired input level fluctuations as rapidly as one would like, and having it undesirably modify amplitude modulation on the signal. Additionally, large and/or abrupt changes in the input level may lead to unacceptable recovery behavior, necessitating further adjustments of the response time.

The issue of excessive loop bandwidth deserves a bit more explanation. If the loop responds too quickly, it will introduce undesired gain modulation arising from the loop's efforts to stabilize the output level of a signal containing legitimate amplitude modulation. This is referred to as "gain pumping." In the context of digital modulation, the presence of appreciable gain pumping can result in significant modulation errors and perhaps even noticeable spectral re-growth in extreme cases. A tolerable value of gain pumping would generally be only a fairly small fraction of 1 dB.

Detector Types (Detector Law)

One convenient aspect of an AGC loop is that the detector need not necessarily have a very wide dynamic range over which it obeys any particular law. This is because the detector operates at a constant average level when the AGC loop is in equilibrium; thus, the detector should only need to cope accurately with the level range associated with a modulated signal. However, as mentioned earlier, the detector's response law (that is linear, log, square law, etc.) can play a significant role in determining the loop's dynamic response during large, abrupt changes in signal level. Perhaps more importantly, the detector's response law influences the dependency of the loop's equilibrium level on the input's waveform or crest factor.

Four detector types will be considered here: envelope detector; square-law detector; true-RMS detector; and log detector.

Envelope Detector (Rectifier)

The output voltage of the envelope detector is proportional to the magnitude of the instantaneous RF input voltage. Assuming that sufficient low pass filtering is applied at its output to eliminate RF ripple, this detector produces a voltage proportional to the envelope amplitude of the RF signal.

Assuming that the loop's bandwidth is made sufficiently small as to avoid significant gain pumping, the effect of the loop using an envelope detector is to stabilize the average rectified voltage of the signal. The resulting power is therefore dependent on the RF signal's envelope waveform. Such a loop acting on a constant-envelope signal such as GSM will produce an average output power which is different than that for a heavily-amplitude-modulated signal, such as CDMA or 64QAM.

The output of the envelope detector cannot go negative no matter how weak the input signal, but may reach extreme positive values in response to very strong signals. Starting with the AGC loop in equilibrium, a sudden large increase in input amplitude causes a very large initial increase in detector output, which very rapidly drives the loop towards lower gain. On the other hand, an abrupt reduction of the input signal level (no matter by how many dB) cannot reduce the detector output below zero, and the loop's best response is to slew towards equilibrium at a fairly low rate until the detector output begins to change by a significant fraction of the reference voltage, at which point the recovery trends towards an exponential decay. In the slew rate limited region, the gain of the signal path is varying at a constant number of dB per second.

Figure 2 shows the behavior of such a loop for a large input level step (note that curves for all four detector types are superimposed on this plot). These results were obtained from simulations in which the VGA has representative limits on the gain range and on the maximum output level. The detectors contrived for these simulations have no particular limits, on the grounds that in most practical situations the designer will scale the circuit so that the detector does not limit appreciably before the VGA does.

Square-law Detector

This type of detector has an instantaneous output which is proportional to the square of the instantaneous RF input voltage, which is equivalent to saying that its output is proportional to input power. This behavior, when incorporated into an AGC loop of sensible bandwidth, makes the loop's equilibrium average output power independent of the input waveform. As with the envelope detector, the output can never go negative, resulting in the loop having a similar tendency towards slew rate limited behavior when reacting to abrupt decreases in input amplitude. The response to large abrupt increases in input amplitude can be even more striking, however, because the square-law detector characteristic exaggerates the effect of the input increase. The extent to which this happens depends on the clipping level of either the VGA or the detector, whichever appears at a lower level.

True-RMS Detector

This detector comprises a square-law detector followed by a low pass filter followed by a square-root function. The low pass filter performs the "mean" operation associated with the root-mean-square (RMS) function, and it should have a sufficiently long time constant to smooth the output variations of the squaring detector that would otherwise arise from the legitimate modulation of the signal.

Because of the square-root element in this detector, the average output is proportional to the signal voltage, not power, so the loop's response to small abrupt decreases or increases of signal level should essentially be the same as that for an envelope detector, provided that the added filter pole within the RMS detector is correctly compensated for elsewhere in the loop. The fact that the added pole is located in a region of the signal path that is square law brings forth the possibility of the large-step response being different from that of the simple envelope detector, which can indeed be seen in the figure. Note that the RMS detector has a slightly slower recovery from a large downward amplitude step than does the standard envelope detector, but a slightly faster recovery (and a bit of overshoot) from a step up in input amplitude. In common with the square-law detector, the true-RMS detector will make the AGC loop's equilibrium point independent of the RF signal waveform.

It should be noted that the presence of the long-time-constant low pass filter in this detector may have a marked influence on loop dynamics; indeed, this filter may even provide the dominant pole in some designs. This time constant must therefore be coordinated with the remainder of the loop design.

LOG Detector

This type of detector produces an output proportional to the logarithm of the RF input voltage. Because this behavior is complementary to that of the linear-in-dB VGA in the loop, the resulting loop dynamics are those of a linear system, assuming that signal level fluctuations during transients remain within the measurement range of the log detector. Subject to that assumption, the AGC loop's response to abrupt large changes in input level will not be slew-rate limited, and will often be faster to recover from amplitude decreases.

As with the envelope detector, the equilibrium point of an AGC loop using the log detector will depend on the RF input waveform.

Comparison of Responses with Different Detectors

The AGC loops whose simulation results are shown were designed so that the small-signal response speeds are identical. The results show that the loop's large-step transient response is markedly dependent on the type of detector. At one extreme, the log detector gives the fastest response to large abrupt decreases in input level because the logarithmic curve has a very steep slope for low inputs, which exaggerates the loop's response. However, the log detector has a shallow slope for high input levels, resulting in a diminished response rate to sudden increases in signal level. At the other extreme, the square-law detector's small slope near zero input level gives it a very sluggish response to large decreases in input amplitude. Conversely, the square-law detector exaggerates the response to large signals, giving the fastest response to increasing signals. The envelope and RMS detectors, having intermediate characteristics, give response speeds in between.

Operating Level of Detector

Ideally the operating level of the detector should be set as high as possible in order to minimize the error due to residual DC offsets. However, other considerations often rule. For signals with amplitude modulation, the peak input to the detector when the loop is in equilibrium must be no higher than what the detector will support, and so the average must be lower. Even for constant-envelope signals, the average level must be reasonably lower than the maximum, so that there is room for the detector level to increase if the system input level increases; otherwise, there could be little or no error signal to drive the loop back towards equilibrium. Note that there will generally be unequal amounts of room for the detector output to swing up or down from the design equilibrium level, which will make the apparent attack and decay speeds of the loop differ.

Design Example of a Working AGC Loop

Let's now put the above considerations to work in a practical design. The design assumptions and goals are as follows:

• Signal modulation : W-CDMA (15 users); symbol rate = 3.84 Msymbols/s
• IF frequency : 380 MHz
• VGA : AD8367
• Detector : AD8361 (true RMS, for waveform independence)
• Power supply : 5 VDC

From these, reasonable constraints will be established for operating levels to maximize the adjacent channel power ratio (ACPR) and AGC loop bandwidth (to avoid excessive gain pumping).

Previous bench measurements on the AD8367 had revealed that the best ACPR at 380 MHz occurs with an output level of about 112 mV_rms, which gives about -12 dBm into 200 .

Detector Operating Level

The peak-to-average power ratio for the chosen signal is about 18 dB. When operating from a 5 V supply, the maximum output level of the AD8361 is about 4.8 V (from the AD8361 datasheet). The squarer in the detector will be assumed to go into clipping at the same input level that results in maximum output, for a CW signal. Thus, assuming that the peaks of the modulated signal should not drive the detector's squarer into clipping when the loop is in equilibrium, the average output level of the detector must be such that it is at least 18 dB below 4.8 V; 4.8 x 10^-18/20 = 604 mV. Since the conversion gain of the detector is 7.5 V/V_rms, the loop-equilibrium level at the detector's input should be 604 mV/7.5 = 80 mV_rms.

This level can be obtained from the desired output level of the VGA by adding a series resistor of 90 , which combines with the 225 input resistance of the AD8361 to form a voltage divider that achieves the desired result. Note that this loads the output of the VGA with 315 , which means that the lowest additional parallel load impedance on the VGA would be 547 in order to satisfy its design minimum load impedance of 200 . However, in this case more than half of the VGA's power output is going to be feeding the detector. This could be remedied by driving the VGA end of the 90 resistor with an emitter follower, raising the input impedance of the overall detector by the beta of the transistor used in the follower. This would free up almost all the output current capability of the VGA for use by the useful load.

Estimation of Target AGC Loop Bandwidth

Here a judgment call must be made, based on an empirical measurement, to establish the maximum loop bandwidth that will avoid intolerable gain pumping. For purposes of this design example, it is assumed that up to 0.5 dB p-p gain variation is acceptable. An estimate of the desired loop bandwidth will be made by passing a W-CDMA signal through a spectrum analyzer with very wide resolution bandwidth, zero span and linear detector, and observe what video bandwidth results in 0.5 dB p-p output variation. The result turns out to be 200 Hz, which means the initial design of the AGC loop will have a 200 Hz bandwidth. The simulation and measured results will be used to see how this choice works out.

RMS Detector Filter

The RMS detector's "mean value" filter comprises an internal filter resistance combined with an external shunt capacitance. The effective value of the filter resistance varies with drive level, from about 2000 at very low drive level down to about 500 at maximum drive level. For this example a value of 1.8 k will be used, which was determined empirically for the operating level established earlier.

In general, an AD8361 would be taken into the lab with a W-CDMA signal source in order to ascertain a suitable filter capacitor value. However, the previous measurement for loop bandwidth gives a clue that allows a reasonable estimate of the required value to be made. A loop bandwidth of 200 Hz resulted in a 0.5 dB p-p (~6 percent) variation of detector output. It so happens that this is just about the maximum amount of variation of RMS filter level that still gives good RMS accuracy. So, the bandwidth of this filter will simply be made equal to 200 Hz, which requires a filter capacitor of about 0.44 µF against the 1.8 k filter resistance.

Loop Dynamics Design

A first order loop will be developed, with a small-signal bandwidth of 200 Hz. Note that the RMS detector's filter already contributes one pole at 200 Hz, so the remainder of the loop will clearly need to take this into account. This will be achieved by choosing R_comp to create a zero at 200 Hz in conjunction with C_integ (see Appendix A ). The response speed of all the other elements in the loop is so much faster than that of the desired loop that all other poles can be safely ignored.

The loop bandwidth designed will apply only for small deviations from the AGC loop's equilibrium level. Large transients will behave differently because of the nonlinear character of the loop, and simulation and/or breadboarding will be relied upon to investigate the large signal behavior.

The next items on the agenda are the determinations of the incremental gains of the VGA and of the detector from the loop dynamics viewpoint. For the VGA, this means the slope of V_out versus control voltage, not the RF gain.

VGA Gain

V_in and V_out will represent RMS values of the VGA's RF input and output, respectively, and V_g will represent the gain control voltage. From examination of the AD8367 performance data in the datasheet for 240 MHz, combined with a bit of extrapolation and rounding, 0 dB of gain is found to occur at a control voltage of 0.1 V and the control slope is 50 dB/V. By formulating and then differentiating V_out with respect to V_g at the equilibrium output of 112 mV_rms, the incremental slope is evaluated to be 0.6447 V_rms/V.

Next the Detector Slope

The nominal conversion gain of the AD8361 is 7.5. However, a 90 series resistor was added at the input of the detector; this has the effect of reducing the detector's effective gain to 5.357, which is the value that will be used in the loop analysis.

Avoidance of Excessive Recovery Delay

If the loop is left sitting with a very low (or zero) input signal level for a time, the output voltage of the integrator will continue to rise until it reaches saturation of the op-amp as the loop tries to find more gain. When a significant signal does suddenly arrive at the system input, one has to wait for the integrator's output to ramp back down to 1 V before the loop can begin reducing the gain. To reduce this "overload delay" a 4.3:1 attenuator is inserted between the integrator and the control input of the VGA so that the positive limit (nearly 5 V) of the integrator's output is about equal to the maximum effective control input (1 V) to the VGA.

Calculation of Component Values

In the loop, a net gain (excluding the integrator for the moment) of 0.644 (VGA incremental slope) · 5.357 (effective detector slope)/4.3 (for the V_agc atten) = 0.803, is obtained. For a loop bandwidth of 200 Hz, the loop gain should be unity at that frequency. If the rest of the loop has a gain of 0.803, the integrator must have a gain of 1.0/0.803 = 1.245, which requires that the reactance of C_integ at 200 Hz be 1.245 times the value of R_in. Mathematically, 1/(2 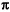· 200 · C_integ) = 1.245 · R_in; R_in · C_integ = 639.2 µs.

Now another constraint must be also noted, which is that the AD8361 cannot source very much current, and can sink even less. Therefore, 50 k is chosen for R_in in order to minimize total loading on the AD8361's output, which leads to a value of 12.78 nF for C_integ. Finally, in order to compensate for the 200 Hz pole in the RMS detector, R_comp is chosen as 62.3 k to provide a loop zero at 200 Hz with C_integ. A 10 k pulldown is also added on the AD8361's output to improve its effective sinking capacity.

Lab Tests

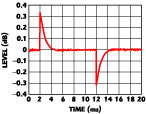
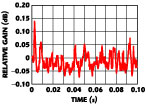
A prototype circuit was constructed according to the schematic in Appendix A. Figures 3 and 4 show the prototype loop's response to small and large (30 dB) input level steps, respectively. Figure 5 shows the measured gain pumping obtained by capturing the signal at the gain-control input of the VGA with an oscilloscope and scaling into dB.

Conclusion

Numerous basic and finer points of AGC design have been discussed, and a detailed example of a practical design was worked out. Practical considerations and difficulties encountered along the way were emphasized, as opposed to reiterating textbook loop design equations. Finally, a working circuit was constructed and measurement results presented.

Appendix A Schematic of Breadboard of Example Circuit Using a True-RMS Detector.